
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи, рассмотренные на Лекции и Семинаре 14Содержание книги
Поиск на нашем сайте
Задача 1–Т14. Рассмотрим распределение футбольных матчей Первенства России по числу забитых мячей в 1996 году. Представление об этом дает следующая таблица. Вычислить среднюю результативность матчей. Ответ: 2,62 за игру.
Задача 2-Т14. На соревнованиях по фигурному катанию 2 фигуристки получили (по шестибальной шкале) оценки судей, представленные в таблице:
Какая из фигуристок выступила лучше?
Задача 3-Т14. Имеются: 1) распределение СВ Х – число прочитанных за каникулы книг десятью девочками по частотам (М)
2) распределение по частотам СВ Y – число прочитанных за каникулы книг девятью мальчиками того же класса.
Нужно сравнить интерес к чтению девушек и юношей.
Задача 4-Т14. Вычислить медиану выборки: 9, 3, 5, 8, 4, 11, 13.
Задача 5–Т14. Найти медиану выборки 20, 9, 13, 1, 4, 11.
Задача 6–Т14. Предлагается следующая азартная игра. Бросают два игральных кубика. Если полученная сумма очков больше 10, то игрок выигрывает 10 копеек, в противном случае он проигрывает 1 копейку. Имеет ли смысл играть в эту игру 12.000.000 партий?
Задача 7–Т14. Предприниматель размышляет над тем, куда лучше вложить деньги – купить киоск для торговли мороженым или палатку для торговли хлебобулочными изделиями. Вложение денег в торговлю мороженым с вероятностью 0,5 обеспечит годовую прибыль в 5.000 долларов, с вероятностью 0,2 – 10.000 долларов, и с вероятностью 0,3 – 3.000 долларов. Для торговли хлебобулочными изделиями прогноз таков: 5.500 долларов с вероятностью 0,6; 5.000 долларов с вероятностью 0,3 и 6.500 долларов с вероятностью 0,1. В каком случае (торговля мороженым или хлебобулочными изделиями) математическое ожидание дохода больше?
Задача 8–Т14 СВ Х и У заданы таблично. Вычислить дисперсии величин Х и У.
Задача 9–Т14. Равны ли дисперсии случайных величин 2 Х и Х + Х?
Задача 10–Т14. На испытательном стенде оружейного завода пристреливают готовые ружья, т.е. уточняют и корректируют их прицел. В таблице приведены измерения горизонтальных отклонений (в сантиметрах) от цели при стрельбе трех ружей. Найти средние, дисперсию результатов испытания для ружей А, Б и В. Какое из ружей более точное?
Задача 11–Т14. Пусть M (X) = 5,6; D (X) = 3,04. Вычислить M (Y) и D (Y), если Y = 3 x + 2.
Задача 12–Т14. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины
Задача 13–Т14. В таблице приведен закон распределения случайной дискретной величины X, которая может принимать 5 значений. Найти: а) её числовые характеристики; б) функцию распределения; в) вероятность того, что X примет значение меньше M (X); г) вероятность того, что X примет значение больше 0,5 M (X).
Домашнее задание 14. Тема 14 – Числовые характеристики случайной величины. Закон распределения СВ
Задача 1Д-Т14. Ученик выписал из дневника свои отметки за март месяц. У него получилось: 4, 4, 3, 2, 5, 3, 3, 4, 5, 4, 4, 4, 5, 4, 2, 4, 4, 5, 3, 3. а) Составить сгруппированный ряд этих данных. б) Чему равны размах, медиана и мода этого измерения и какова ее кратность? в) Выпишите таблицу распределения данных. г) Найдите среднее отметок за март, дисперсию этой оценки.
Задача 2Д-Т14. В очередном туре футбольного чемпионата состоялись 10 матчей. Вот из результаты: 3: 1; 0: 2; 1: 1; 0: 0; 0: 4; 0: 1; 2: 2; 0: 3; 1: 0; 1: 1. Футбольный статистик подсчитал результативность матчей (количество голов). а) Выпишите несгруппированный ряд полученных данных. б) Сгруппируйте его и составьте таблицу распределения данных и распределение их частот в процентах. в) Постройте гистограмму распределения данных. г) Найдите среднюю результативность матчей в этом туре, а также дисперсию результата.
Задача 3Д-Т14. Лидеру партии принесли сводку данных о проголосовавших за его партию по пяти избирательным участкам одного округа:
а) Найдите среднее результатов в процентах. б) Подсчитайте общее количество голосовавших на этих пяти участках. в) Подсчитайте число проголосовавших за партию на каждом участке. г) Пройдет ли партия 7%-ный барьер в этом округе?
Задача 4Д-Т14. Измеряется длина слов в отрывке из поэмы А.С. Пушкина «Медный всадник». Составьте ряд данных и постройте гистограмму распределения этих данных. «… Ужасен он в окрестной мгле! Какая дума на челе! Какая сила в нем сокрыта! А в сем коне какой огонь! Куда ты скачешь, гордый конь, И где опустишь ты копыта?...»
Задача 5Д-Т14. По приведенным данным из сводной таблицы распределения результатов некоторого измерения:
а) найдите х; б) найдите у; в) восстановите всю таблицу; г) найдите моду этого распределения.
Задача 6Д-Т14. Рассматриваются оценки, полученные выпускниками одной из школ за сочинение. Выставлялись две оценки: первая – по литературе, вторая – по русскому языку. Отметки эти таковы: 5/4; 4/5; 3/1; 4/3; 2/3; 3/3; 4/3; 5/3; 3/3; 1/2; 4/4; 4/2; 2/1; 3/5; 3/4; 4/3; 5/5; 4/4; 5/4; 2/2; 2/3; 4/3; 2/3; 3/3. 1) Для отметок по литературе, а также (аналогично) для отметок по русскому языку: а) выпишите сгруппированный ряд данных; б) составьте таблицу распределения кратностей; в) постройте многоугольник распределения процентных частот; г) найдите среднее значение. 2) а) вычислите размах, моду, медиану, дисперсию и среднее квадратичное распределения отметок по литературе; б) вычислите размах, моду, медиану, дисперсию и среднее квадратичное распределения отметок по русскому языку; в) по какому предмету отметки в среднем выше? г) по какому предмету отметки имеют более устойчивый характер?
Задача 7Д-Т14. Научно-педагогический стаж (в годах) восьми преподавателей кафедры Психологии составил: 5, 8, 15, 12, 17, 14, 18, 9 лет. Найти среднее, моду, медиану, математическое ожидание, дисперсию и СКО этой выборки.
Задача 8Д-Т14. Студентки-первокурсницы на соревнованиях по легкой атлетике взяли высоты, величина которых составила (в см): 90, 125, 125, 130, 130, 135, 135, 135, 140, 140, 140. Какая высота прыжка наилучшим образом характеризует спортивную подготовку девушек?
Задача 9Д-Т14. В таблице приведены данные о рабочем стаже (в годах) сотрудников лаборатории. Найти среднее, моду, медиану, математическое ожидание, дисперсию и СКО рассматриваемой совокупности.
Задача 10Д-Т14. Найти математическое ожидание, дисперсию и СКО СВ Х, заданной законом распределения:
Задача 11Д-Т14. Пусть Х и Y – независимые дискретные СВ, причем МХ = 2, МY = -3, DX = 2, DY = 9. Найти MZ и DZ, если
Задача 12Д-Т14. Игроку предложена следующая игра: он (игрок) бросает игральную кость и получает столько $, сколько выпало очков. Цена игры составляет 4$. Выгодно ли играть в такую игру?
Задача 13Д-Т14. Решить уравнения: а) б) в) г) д) е) ж) з)
Задача 14Д-Т14. Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,2. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. а) составить закон распределения числа очков, полученных стрелком за три выстрела; б) определить математическое ожидание, дисперсию и стандартное отклонение.
Задача 15-Т14. В билете три задачи. Вероятность правильного решения первой задачи равна 0,9, второй задачи – 0,8, третьей задачи – 0,7. Составить закон распределения числа правильно решенных задач в билете. Определить математическое ожидание и дисперсию.
Тема 15. Случайные величины с бесконечным числом значений. Непрерывные случайные величины. Плотность распределения. Нормальное распределение. – 4 часа: 2 часа лекции, 2 часа семинарское занятие
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.242.160 (0.006 с.) |

 , заданной рядом распределения:
, заданной рядом распределения: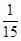

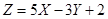 .
. ;
;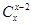 = 15;
= 15;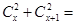 49;
49; = 70;
= 70;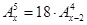 ;
;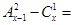 79;
79;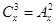 ;
; .
.


