
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как вычислять факториал? Формула СтирлингаСодержание книги
Поиск на нашем сайте
Если абсолютная точность не требуется, для вычисления факториала при
Задачи, рассмотренные на Лекции и Семинаре 3. Тема 3. Элементы комбинаторики: Перестановки, Размещения, Сочетания Лекция 3 Задача 1-Т3. Составить различные перестановки из элементов множества Е = {2, 7, 8}. Подсчитайте их число.
Задача 2-Т3. Сколькими способами можно распределить пять должностей между пятью лицами, избранными в президиум спортивного общества.
Задача 3-Т3. Сколькими способами можно расставить на полке 5 различных книг?
Задача 4-Т3. Сколько различных чисел можно составить из четырех цифр 0, 1, 2, 3, если ни одна из цифр не будет повторяться?
Задача 5-Т3. Сколькими способами можно разложить m = 2 пронумерованных шара в n = 4 пронумерованные корзины так, чтобы в каждой корзине оказалось не более одного шара?
Задача 6-Т3. Сколько различных трехзначных чисел можно составить из нечетных цифр 1, 3, 5, 7, 9, если каждую цифру использовать только один раз?
Задача 7-Т3. Составить различные размещения по 2 из элементов множества D = {а, b, c} и подсчитать их число.
Задача 8-Т3. Найти число размещений из четырех элементов a, b, c, d по два.
Задача 9–Т3. В Президиум собрания избраны 8 человек. Сколькими способами они могут распределить между собой обязанности Председателя, секретаря и счетчика?
Задача 10-Т3. Сколькими способами можно выбрать из четырех корзин – две?
Задача 11–Т3. Сколькими различными способами можно избрать из 10 человек комиссию в составе трех человек?
Задача 12-Т3 (для самостоятельного решения). Из восьми намеченных кандидатов следует избрать трех счетчиков, которые будут участвовать в переписи населения. Сколькими способами это можно сделать?
Задача 13-Т3. Сколькими способами можно выбрать из четырех пронумерованных корзин – три шара?
Задача 14-Т3. Составить различные сочетания по 2 из элементов множества D = {a, b, c}. Подсчитайте их число.
Задача 15-Т3. В лотерее нужно зачеркнуть любые 8 чисел из 40. Сколькими способами это можно сделать?
Задача 16-Т3. В партии из 23 деталей 10 бракованных. Вынимают наугад две детали из партии. Определить вероятность того, что обе детали окажутся бракованными.
Семинар 3 Задача 1С-Т3. В урне содержится 5 белых и 4 черных шара, различающихся только цветом. 1) Вынимается наудачу один шар. Найти вероятность того, что он белый. 2) Вынимаются наудачу два шара. Найти вероятность того, что: а) оба шара белые; б) хотя бы один из них черный.
Задача 2С-Т3. Сколькими способами можно расставить на книжной полке десятитомник Джека Лондона, располагая их: а) в произвольном порядке; б) так, чтобы I, V и IX тома стояли рядом (в любом порядке); в) так, чтобы I,II и III тома не стояли рядом (в любом порядке).
Задача 3С-Т3. Сколькими способами можно выбрать три цветка из вазы, в которой стоят 10 красных и 4 розовые гвоздики? А если выбрать одну красную гвоздику и две розовые?
Задача 4С-Т3. На десяти карточках написаны цифры 0, 1, 2, …, 9. Берут четыре карточки и составляют из цифр, написанных на них, число. Сколько различных четырехзначных чисел можно составить таким образом?
Задача 5С-Т3 (для самостоятельного решения). Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры не повторяются?
Задача 6С-Т3. Дано шесть карточек с буквами Н, М, И, Я, Л, О. Найти вероятность того, что: а) получится слово «ЛОМ», если наугад, одну за другой, выбираются три карточки; б) получится слово «МОЛНИЯ», если наугад, одна за другой, выбираются шесть карточек и располагаются в порядке их появления.
Задача 7С-Т3. Сколько различных правильных дробей можно составить из чисел 3, 5, 7, 11, 13, 17, 19, 23, так, чтобы в каждую дробь входило два числа?
Задача 8С-Т3. Некто забыл нужный ему номер телефона, который состоит из одной из десяти букв и пяти цифр, но он помнит, что в образовании этого номера участвовали цифры 2, 3, 6, 7. Какое наибольшее число проб надо сделать, чтобы дозвониться нужному абоненту?
Задача 9С-Т3. Человек забыл две последние цифры в шестизначном телефонном номере, помнит только, что они были неодинаковые и нечетные. Сколько таких телефонных номеров может быть?
Задача 10С-Т3. В конверте среди 25 карточек находится разыскиваемая карточка. Из конверта наудачу извлечено 6 карточек. Какова вероятность, что среди них окажется нужная карточка?
Задача 11С-Т3. Сколькими способами можно из 40 человек, поступающих в вуз, создать 4 группы разных специальностей по 10 человек в каждой?
Задача 12С-Т3 (дополнительная). Из колоды, содержащей 36 карт, наудачу вынимают три карты. Найти вероятность того, что среди них окажется хотя бы одна дама.
Домашнее задание 3 – Тема 3.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 771; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.153.171 (0.009 с.) |

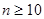 можно использовать приближённую формулу Стирлинга:
можно использовать приближённую формулу Стирлинга:



