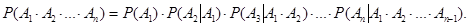Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы вероятности суммы и произведения событийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 1Д-Т6. Вероятность выполнения данных обещаний одной бригадой строителей равна 0,9, а второй – 0,95. Какова вероятность того, что хотя бы одна бригада выполнит свои обязательства, если они работают независимо друг от друга?
Задача 2Д-Т6. Вероятность поражения цели стрелком при каждом выстреле составляет 0,7. Производится 4 независимых выстрела. Какова вероятность того, что первые два выстрела будут промахи, а последующие два – попадания?
Задача 3Д-Т6. Известно, что при каждом измерении возможна как положительная, так и отрицательная ошибка. Какова вероятность того, что при пяти независимых измерениях все ошибки будут положительными?
Задача 4Д-Т6. В одном ящике имеется 12 однотипных деталей, из которых 4 нестандартные, в другом – 15 деталей, из которых 3 нестандартные. Из каждого ящика наудачу извлекается по одной детали. Найти вероятность того, что обе детали окажутся нестандартными.
Задача 5Д-Т6. Два стрелка независимо друг от друга стреляют по одному разу в мишень. Вероятность попадания в цель у первого стрелка составляет 0,8, а у второго – 0,7. Какова вероятность того, что мишень будет поражена хотя бы одним стрелком?
Задача 6Д–Т6. Брошены две монеты. Какова вероятность того, что появятся: а) два Орла? б) Орел и Решка?
Задача 7Д–Т6. Стрелок ведет огонь по цели, движущейся на него. Вероятность попадания в цель при первом выстреле 0,4 и увеличивается при каждом следующем выстреле на 0,1. Какова вероятность получить два попадания при трех выстрелах?
Задача 8Д-Т6. Монета подбрасывается 4 раза. Какова вероятность того, что при этом хотя бы один раз появится герб?
Задача 9Д-Т6. Профсоюзной организацией для детей, выезжающих летом на отдых, выделено 12 путевок в пионерский лагерь, 8 – в туристический и 5 – в военно-спортивный. Какова вероятность того, что три друга попадут в один лагерь, если их родители независимо друг от друга приобрели по одной путевке?
Задача 10Д-Т6. Вероятность бесперебойной работы первого станка в течение часа равна 0,75, а второго – 0,8. Какова вероятность того, что в течение часа будет нарушение в работе только одного станка, если станки работают независимо друг от друга.
Задача 11Д-Т6. Из колоды в 36 карт наудачу извлекается одна карта. Вводятся события:
А = {извлеченная карта является Тузом}, В = {извлечена карта черной масти}, С = {извлеченная карта является «фигурой», т.е. Валетом, Дамой, Королем, Тузом}. Установить, зависимы или не зависимы следующие пары событий: А и В, А и С, В и С. Определить, используя формулу вероятности произведения, вероятность события А·В·С.
Задача 12Д-Т6. Из 100 студентов, находящихся в аудитории, 50 человек знают английский язык, 40 – французский язык, 35 – немецкий язык. Английский и французский знают 20 студентов, английский и немецкий – 8 человек, французский и немецкий – 10 человек. Все три языка знают 5 человек. Один из студентов вышел из аудитории. Введем события: А = {вышедший знает английский язык}, В = {вышедший знает французский язык}, С = {вышедший знает немецкий язык}. Указать все пары независимых событий. Установить, являются ли события А, В, С независимыми в совокупности.
Задача 13Д-Т6. Три студента делают некоторый расчет. Вероятность ошибиться для первого студента составляет 0,1; для второго – 0,15; а для третьего – 0,20. Найти вероятности следующих событий: А = {все студенты выполнили расчет верно}, В = {только два студента выполнили расчет верно}, С = {хотя бы один студент допустил ошибку в расчете}.
Задача 14Д-Т6. Игроки А и В разыгрывают денежный приз в следующей игре. Подбрасывается монета до тех пор, пока не выпадет шесть Гербов или шесть Решек. Если выпало шесть Гербов, то выигрывает игрок А, если шесть Решек – игрок В. Монету подбросили 8 раз. При счете 5:3 в пользу игрока А (т.е. выпало 5 Гербов и 3 Решки) игра прервалась по не зависящим от игроков причинам. В каком отношении следует разделить приз?
Задача 15Д–Т6. Вероятность того, что наудачу названный студент сдаст экзамен по антропологии составляет 0,9, второй экзамен по общей психологии – 0,8, а третий экзамен по теории вероятностей – 0,7. Какова вероятность того, что студент сдаст хотя бы один экзамен, если считать экзамены независимыми друг от друга?
Тема 7. Независимость событий. Условные вероятности. – 4 часа: 2 часа лекции, 2 часа семинарское занятие
Условные вероятности Пусть А и В – два события, рассматриваемых в опыте, при этом наступление одного события (А) может повлиять на возможное наступление другого (В). Для характеристики зависимости одних событий от других вводится понятие условной вероятности.
Определение. Условной вероятностью события В при условии, что произошло событие А, называется отношение вероятности произведения этих событий к вероятности события А, причем Таким образом, по определению:
Вероятность Аналогично определяется условная вероятность события А при условии В, т.е.
Теорема 1 (правило умножения вероятностей). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло: Р (А·В) = Р (А) Р(В | A) или Р (А·В) = Р (В) Р(А | B). Если Аналогично, если
Лемма о взаимной независимости событий. Если событие А не зависит от события В, то и событие В не зависит от события А. Если события А и В не являются независимыми, то в формулах вероятности суммы и произведения используют формулу условной вероятности:
или
Условная вероятность 1) 2) 3) Эти формулы для определения вероятности суммы и произведения событий справедливы для любого количества составляющих элементарных событий. В случае n событий:
Например, в случае трех составляющих:
Полезный алгоритм 1. Уяснить, в чем состоит испытание, рассматриваемое в задаче. 2. Обозначить события, рассматриваемые в задаче. 3. С помощью введенных обозначений выразить искомое событие. 4. Если необходимо найти вероятность суммы событий, то необходимо выяснить, являются ли рассматриваемые события совместными или несовместными. 5. Если необходимо найти вероятность произведения событий, то следует выяснить, являются ли эти события независимыми / зависимыми. 6. Выбрать соответствующие условию задачи формулы и произвести вычисления. 7. Если вероятности рассматриваемых событий не даны в условиях задачи, то их следует предварительно вычислить.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.110.63 (0.01 с.) |

 ≠ 0. Условная вероятность обозначается
≠ 0. Условная вероятность обозначается 

 в отличие от условной вероятности
в отличие от условной вероятности  , называется безусловной вероятностью.
, называется безусловной вероятностью.
 , то наступление события А не изменяет вероятности наступления события В. В этом случае говорят, что событие В независимо от события А.
, то наступление события А не изменяет вероятности наступления события В. В этом случае говорят, что событие В независимо от события А. , то наступление события В не изменяет вероятности события А, т.е. событие А является независимым от В.
, то наступление события В не изменяет вероятности события А, т.е. событие А является независимым от В.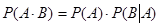

 и это очевидно;
и это очевидно;
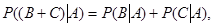 если
если  Ø, поэтому
Ø, поэтому