
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Независимость событий. Условная вероятностьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задачи, рассмотренные на лекции и семинаре 7 Лекция 7
Задача 1-Т7. Какова вероятность того, что наугад вынутая из полного набора костяшка домино окажется дублем, если известно, что сумма очков на этой костяшке меньше, чем 5?
Задача 2–Т7. Пусть в группе студентов, состоящей из 20 юношей и 15 девушек, 10 человек занимаются стрелковым спортом. Среди этих стрелков 4 девушки. Наудачу выбирается 1 студент. Пусть стало известно, что он занимается стрелковым спортом. Как после этого изменится вероятность того, что выбранной оказалась девушка?
Задача 3–Т7. Из полного набора костяшек домино дважды наудачу вынимают по одной костяшке, не возвращая их в игру. Найти вероятность появления дубля при втором испытании, если в первый раз был извлечен не дубль.
Задача 4-Т7. В лаборатории 7 женщин и трое мужчин. Случайным образом из числа этих сотрудников для участия в научной конференции выбирается один докладчик и один содокладчик. Какова вероятность того, что докладчиком будет выбрана женщина, а содокладчиком – мужчина?
Семинар 7 Задача 1С–Т7. В урне 2 белых и 7 черных шаров. Из нее последовательно вынимается два шара. Какова вероятность того, что второй шар окажется белым, при условии, что первый шар был черным?
Задача 2С–Т7. Абонент забыл последнюю цифру номера телефона и набирает ее наудачу. Определить вероятность того, что он наберет нужный номер не более, чем за три попытки?
Задача 3С-Т7. В библиотеке на стеллаже в случайном порядке расставлены книги: десять учебников по экономике и пять – по математике. Библиотекарь наудачу берет три учебника. Найти вероятность того, что хотя бы один из взятых библиотекарем учебник будет учебником по математике.
Задача 4С–Т7. В коробке находятся 4 белых, 3 синих и 2 черных шара. Наудачу последовательно вынимают 3 шара. Какова вероятность того, что первый шар будет белым, второй – синим, а третий – черным?
Задача 5С–Т7 (дополнительно). В первой урне находятся три белых, пять красных и семь синих шаров. Во второй урне находятся два белых, четыре красных и девять синих шаров. Из каждой урны наудачу извлекают по одному шару. Найти вероятность того, что оба извлеченных шара будут одного цвета.
Домашнее задание 7 - Тема 7. Независимость событий. Условные вероятности
Задача 1Д–Т7. Опыт состоит в последовательном подбрасывании монеты два раза. Рассматриваются события: А = {первый раз выпадает Герб}, В = {второй раз выпадает Герб}, С = {Герб выпадает хотя бы один раз}, D = {Решка выпадает хотя бы один раз}. Определить зависимы или независимы пары событий А и В, А и D, В и С, С и D.
Задача 2Д-Т7. На одинаковых карточках написаны натуральные числа от 1 до 25 включительно. Наудачу дважды извлекается по одной карточке без возвращения. Какова вероятность того, что на обеих карточках будут написаны простые числа?
Задача 3Д-Т7. В урне находится 100 лотерейных билетов, из которых 25 выигрышных. Из урны трижды без возвращения извлекают по одному билету. Какова вероятность того, что все три билета окажутся выигрышными?
Задача 4Д-Т7. В коробке находятся 2 красных, 3 синих и 2 зеленых карандаша. Из нее наудачу берут без возвращения три раза по одному карандашу. Найти вероятность того, что красный карандаш появится раньше синего.
Задача 5Д–Т7. Студент знает 20 из 25 вопросов программы. Зачет считается сданным, если студент ответит не менее чем на три из четырех предложенных вопросов. Какова вероятность того, что: а) студент сдаст зачет? б) зачет будет сдан, если на первые два вопроса студент уже ответил верно?
Задача 6Д-Т7. На столе лежат 4 синий и 3 красных карандаша. Редактор дважды наугад берет по одному карандашу и обратно их не кладет. Найти вероятность того, что: а) вторым был взят красный карандаш при условии, что первым был взят синий; б) вторым взят синий карандаш при условии, что первым оказался синий; в) вторым взят синий карандаш при условии, что первым был красный; г) вторым взят красный карандаш, при условии, что первым также оказался красный карандаш.
Задача 7Д-Т7. В барабане находится 10 лотерейных билетов, из них два выигрышных. Из барабана вынимают два раза по одному билету, не возвращая их обратно. Какова вероятность того, что: а) второй раз был извлечен билет без выигрыша при условии, что первым оказался выигрышный билет? б) первый раз вынут выигрышный билет, а второй – билет без выигрыша?
Задача 8Д-Т7. Из ящика, содержащего 4 белых и 5 красных шаров, два раза наугад извлекают по одному шару, не возвращая их обратно. Найти вероятность того, что: а) вторым извлечен красный шар при условии, что первым оказался также красный шар? б) оба раза извлекались красные шары?
Задача 9Д-Т7. Из колоды в 36 карт последовательно наугад вынимаются и не возвращаются 2 карты. Какова вероятность того, что: а) оба раза извлекались карты красной масти? б) первой была вынута карта красной масти, а второй – черной масти? в) второй вынута карта черной масти при условии, что первой была карта красной масти?
Задача 10Д-Т7. В цехе работают 10 мужчин и три женщины. По табельным номерам последовательно наугад выбирают 2 человека для делегирования на профсоюзную конференцию. Какова вероятность того, что: а) выбранными окажутся две женщины? б) выбранными окажутся двое мужчин? в) первым выбран мужчина, а второй – женщина? г) вторым выбран мужчина при условии, что первым также был мужчина?
Задача 11Д-Т7. Студент, идя на экзамен, знал ответы на 25 билетов из 30, предлагаемых экзаменатором. На первый билет студент не знал ответа и, не возвращая его экзаменатору, вытянул второй билет. Какова вероятность того, что: а) вторым ему достался билет, на который он знал ответ? б) вторым ему достался билет, на который он не знал ответа?
Задача 12Д-Т7. Студент, которому предстояло сдавать зачет, знал ответы на 70 вопросов из 90. Какова вероятность того, что он: а) верно ответит на два вопроса? б) ответит на второй вопрос при условии, что он не знал ответа на первый вопрос?
Задача 13Д-Т7. В розыгрыше первенства страны по волейболу участвуют 18 команд, из которых случайным образом формируют две группы по 9 команд в каждой. Среди участников первенства имеется 5 команд экстра-класса. Найти вероятность того, что все команды экстра-класса попадут в одну и ту же группу.
Задача 14Д-Т7. Брошено две игральные кости. Предполагается, что все комбинации выпавших очков равновероятны. Найти условную вероятность того, что выпали две пятерки, если известно, что сумма выпавших очков делится на 5. Задача 15Д-Т7. Решить уравнение относительно n:
Задача 16Д-Т7. Решить уравнение относительно m.
Задача 17Д-Т7. Решить уравнение относительно n.
Дополнительные задачи Задача Д1. Из колоды карт (36 карт) вынимают наудачу карту. Чему равна вероятность того, что эта карта окажется Тузом?
Задача Д2. Предположим теперь, что вынутая карта оказалась черной. Чему равна условная вероятность вынуть Туза при этом условии?
Задача Д3. Нарисуйте два подмножества квадрата, такие, что два события: попадание в каждое из этих множеств при стрельбе по квадрату — будут независимыми.
Задача Д4. События А и В независимы. Являются ли независимыми события: а) А и В, б) Тема 8. Формула полной вероятности. – 4 часа: 2 часа лекции, 2 часа семинарское занятие
Одним из эффективных способов подсчета вероятностей является формула общей вероятности, являющаяся следствием формул вероятностей суммы и произведения событий. Предположим, что событие A может наступить лишь при появлении одного из попарно несовместных событий H 1, H 2,..., Hn. По отношению к событию А будем называть их гипотезами. Пусть H 1, H 2,..., Hn образуют полную группу. Тогда появление события А связано с обязательным наступлением ровно одного из событий А
Поскольку вероятность суммы несовместных событий равна сумме вероятностей событий-слагаемых, то
Формула условной вероятности
Тогда переписываем последнее равенство в виде:
Таким образом, вероятность события A определяется как сумма произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A. Это и есть формула полной вероятности, которую можно использовать при подсчете вероятностей конкретных событий.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 993; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.196.68 (0.01 с.) |

 .
. 



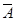 и
и  ?
?
 …,
…,  , и событие А можно представить в виде:
, и событие А можно представить в виде: .
. .
. в этом случае для любого i =
в этом случае для любого i =  будет выглядеть следующим образом:
будет выглядеть следующим образом: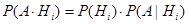 .
.



