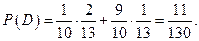Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретное и произвольное пространство элементарных событийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Дискретное вероятностное пространство. Классическое определение вероятности Определение. Событием называется всякий факт, который может произойти или не произойти в результате опыта. Определение. События называются несовместными, если появление одного из них исключает появление других. Классическим примером несовместных событий является результат подбрасывания монеты - выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте). Определение. Полной группой событий называется совокупность всех возможных результатов опыта. Определение. Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта. Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий. Определение. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью. В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров. Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара – событие менее вероятное, чем появление красного. Определение. Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта. Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий:
Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А. Вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей:
Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым. Решение. Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С. Тогда в соответствии с записанными выше формулами получаем:
Вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий. Определение. Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов. Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта. Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна:
Очевидно, эта величина не совпадает с найденной вероятностью. При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события. Классическое определение вероятности неприменимо к испытаниям с бесконечным числом исходов. Чтобы преодолеть этот недостаток вводится понятие геометрической вероятности, т.е. вероятности попадания точки в какой – либо отрезок или часть плоскости (пространства). Так если на отрезке длиной L выделен отрезок длины l, то вероятность попадания наугад взятой точки в отрезок l равна отношению
Операции над событиями
Определение. События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот. Определение. Объединением или суммой событий
Определение. Пересечением или произведением событий
Определение. Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В:
Определение. Дополнительным к событию А называется событие Определение. Среди всех возможных событий 1) все они взаимно исключают друг друга, т.е. являются непересекающимися; 2) в результате данного опыта обязательно происходит одно из этих элементарных событий; 3) каково бы ни было событие Элементарное событие обозначают буквой Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Следствие 1: Если события
Определение. Противоположными называются два несовместных события, образующие полную группу событий. Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Следствие 2: Сумма вероятностей противоположных событий равна единице:
Определение. Событие Определение. Вероятность события
Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило:
Если события независимые, то
В случае произведения нескольких зависимых событий вероятность их совместного появления равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились:
Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события. Если в результате испытания может появиться п событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна:
Здесь событие А обозначает наступление хотя бы одного из событий Пример. Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,875. Найти вероятность попадания в мишень при одном выстреле. Если обозначить р – вероятность попадания стрелком в мишень при одном выстреле, то вероятность промаха при одном выстреле, очевидно, равна Вероятность трех промахов из трех выстрелов равна Получаем: Пример. В первой коробке содержится 10 шаров, из них 8 белых; во второй коробке 20 шаров, из них 4 белых. Из каждой коробки наугад извлекли по одному шару, а затем из этих двух шаров наугад берут один шар. Найти вероятность того, что этот шар белый. Вероятность того, что взятый из первой коробки шар белый - Пример. Имеется пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит цель при выстреле из винтовки с оптическим прицелом, равна 0,95, для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что цель будет поражена, если стрелок произведет один выстрел из наугад выбранной винтовки. Вероятность того, что выбрана винтовка с оптическим прицелом, обозначим Аналогично, вероятность того, что выбрали винтовку без оптического прицела, и при этом цель была поражена Окончательная вероятность поражения цели равна сумме вероятностей
Пример. Последовательно послано четыре радиосигнала. Вероятности приема каждого из них не зависят от того, приняты ли остальные сигналы, или нет. Вероятности приема сигналов равны соответственно 0,2, 0,3, 0,4, 0,5. Определить вероятность приема трех радиосигналов. Событие приема трех сигналов из четырех возможно в четырех случаях:
Для приема трех сигналов необходимо совершение одного из событий А, В, С или D. Таким образом, находим искомую вероятность:
Пример. Двадцать экзаменационных билетов содержат по два вопроса, которые не повторяются. Экзаменующийся знает ответы только на 35 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на два вопроса одного билета или на один вопрос одного билета и на указанный дополнительный вопрос из другого билета. В общей сложности имеется 40 вопросов (по 2 в каждом из 20 билетов). Вероятность того, что выпадает вопрос, на который ответ известен, очевидно, равна Для того чтобы сдать экзамен, требуется совершение одного из трех событий: 1) Событие A – ответили на первый вопрос (вероятность 2) Событие В – на первый вопрос ответили (вероятность 3) Событие С – на первый вопрос не ответили (вероятность Вероятность того, что при заданных условиях экзамен будет сдан равна:
Пример. Имеются две партии однородных деталей. Первая партия состоит из 12 деталей, 3 из которых - бракованные. Вторая партия состоит из 15 деталей, 4 из которых – бракованные. Из первой и второй партий извлекают по две детали. Какова вероятность того, что среди них нет бракованных деталей. Вероятность оказаться не бракованной для первой детали, извлеченной из первой партии, равна Вероятность оказаться не бракованной для первой детали, извлеченной из второй партии, равна Вероятность того, что среди четырех извлеченных деталей нет бракованных, равна:
Пример. Имеются две партии однородных деталей. Первая партия состоит из 12 деталей, 3 из которых - бракованные. Вторая партия состоит из 15 деталей, 4 из которых – бракованные. Из первой партии извлекаются наугад 5 деталей, а из второй – 7 деталей. Эти детали образуют новую партию. Какова вероятность достать из них бракованную деталь? Для того чтобы выбранная наугад деталь была бы бракованной, необходимо выполнение одного из двух несовместных условий: 1) Выбранная деталь была из первой партии (вероятность - 2) Выбранная деталь была из второй партии (вероятность - Таким образом, Пример. В урне 3 белых и 5 черных шаров. Из урны вынимают наугад два шара. Найти вероятность того, что эти шары не одного цвета. Событие, состоящее в том, что выбранные шары разного цвета произойдет в одном из двух случаев: 1) Первый шар белый (вероятность - 2) Первый шар черный (вероятность -
Окончательно: Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта. Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В. Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого. Всего в колоде 13 червонных и 13 бубновых карт. При вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна Пример. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей? Вероятность выпадения 6 очков при одном броске кости равна Тогда вероятность того, что хотя бы один раз выпадет 6 очков, равна Пример. В барабане револьвера находятся 4 патрона из шести в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок два раза. Найти вероятности хотя бы одного выстрела, двух выстрелов, двух осечек. Вероятность выстрела при первом нажатии на курок (событие А) равна Так если в первом случае произошел выстрел, то в барабане осталось только 3 патрона, причем они распределены по 5 гнездам, т.к. при втором нажатии на курок напротив ствола не может оказаться гнездо, в котором был патрон при первом нажатии на курок. Условная вероятность выстрела при второй попытке - Условная вероятность осечки во второй раз - Рассмотрим вероятности того, что во втором случае произойдет выстрел (событие В) или произойдет осечка (событие
Эти четыре случая образуют полную группу событий (сумма их вероятностей равна единице). Анализируя полученные результаты, видим, что вероятность хотя бы одного выстрела равна сумме Теперь рассмотрим другой случай. Предположим, что после первого нажатия на курок барабан раскрутили и опять нажали на курок. Вероятности первого выстрела и первой осечки не изменились - Условная вероятность выстрела при второй попытке - Условная вероятность осечки во второй раз - Тогда:
В этом случае вероятность того, что произойдет хотя бы один выстрел, равна:
Пример. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков. Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие
Вероятность того, что первый стрелок попадет в мишень, а второй – нет равна
Вероятность того, что второй стрелок попадет в цель, а первый – нет равна
Тогда вероятность попадания в цель только одним стрелком равна:
Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:
Тогда вероятность того, что в цель попадет только один стрелок равна:
Пример. Вероятность того, что взятая наугад деталь из некоторой партии деталей, будет бракованной равна 0,2. Найти вероятность того, что из трех взятых деталей 2 окажется не бракованными. Обозначим бракованную деталь – событие А, не бракованную – событие
Если среди трех деталей оказывается только одна бракованная, то это возможно в одном из трех случаев: бракованная деталь будет первой, второй или третьей. Следовательно, искомая вероятность равна:
Окончательно: Пример. Вероятности того, что нужная деталь находится в первом, втором, третьем или четвертом ящике, соответственно равны 0,6, 0,7, 0,8, 0,9. Найти вероятности того, что эта деталь находится: а) не более, чем в трех ящиках; б) не менее, чем в двух ящиках. а) Вероятность того, что данная деталь находится во всех четырех ящиках, равна:
Вероятность того, что нужная деталь находиться не более, чем в трех ящиках равна вероятности того, что она не находится во всех четырех ящиках:
б) Вероятность того, что нужная деталь находится не менее чем в двух ящиках, складывается из вероятностей того, что деталь находиться только в двух ящиках, только в трех ящиках, только в четырех ящиках. Конечно, эти вероятности можно посчитать, а потом сложить, однако, проще поступить иначе. Та же вероятность равна вероятности того, что деталь не находится только в одном ящике и имеется вообще. Вероятность того, что деталь находится только в одном ящике, равна:
Вероятность того, что нужной деталь нет ни в одном ящике, равна:
Искомая вероятность равна
Формула полной вероятности
Пусть некоторое событие А может произойти вместе с одним из несовместных событий Теорема. Вероятность события А, которое может произойти вместе с одним из событий
Доказательство. Так как события
Так как события
При этом Пример. Прибор может работать в нормальном и ненормальном режимах. Нормальный режим наблюдается в 80% всех случаев работы прибора, ненормальный - в 20%. Вероятность выхода прибора из строя за время t в нормальном режиме равна 0,1; в ненормальном- 0,7. Найти полную вероятность выхода прибора из строя за время t. В данном случае гипотеза
По формуле полной вероятности находим искомую вероятность:
Пример. Завод изготавливает изделия, каждое из которых с вероятностью А - изделие будет забраковано; В - изделие будет забраковано в цехе; С - изделие будет забраковано в ОТК завода. Найдём связь между этими событиями. Событие А, очевидно, произойдёт, если произойдёт событие В или С, причём совместно события В и С произойти не могут По теореме сложения вероятностей: Изделие будет забраковано в цехе, т.е. произойдёт событие В при наличии следующих гипотез:
Для того чтобы изделие было забраковано ОТК завода (произошло событие), необходимо, чтобы это изделие имело дефект, и дефект не был обнаружен в цехе. Поэтому по теореме умножения вероятностей Пример 4. Имеются две партии деталей - в одной 10, а в другой 12 шт., причем в каждой из партий - по одной бракованной. Из первой партии во вторую перекладывают одну деталь. Определить вероятность извлечения из каждой партии бракованной детали до перекладывания и после перекладывания. Пусть событие А - извлечение бракованной детали из первой партии, В - из второй до перекладывания, C и D - те же события после перекладывания. Используя классическое определение вероятности находим: При перекладывании имеются две возможности: Вероятности событий А и С одинаковые, т.е. вероятность извлечь бракованную деталь после перекладывания равна такой же вероятности до перекладывания. Это не случайное совпадение, его можно вывести из классических соображений. Действительно, после извлечения первой детали никакой новой информации не получили, и о второй извлекаемой детали известно лишь, что это одна из 10 деталей, первоначально имевшихся в урне, и из 10 возможностей для этой детали имеется одна, что она бракованная. Поэтому
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 734; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

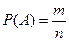 .
. .
.
 .
.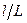 .
.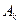 называется событие A, которое означает появление хотя бы одногоиз событий
называется событие A, которое означает появление хотя бы одногоиз событий 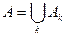 .
. .
.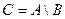 .
. , означающее, что событие А не происходит.
, означающее, что событие А не происходит. , которые в данном опыте которые в данном опыте происходят или не происходят, можно выделить совокупность так называемых элементарных событий, обладающих следующими свойствами
, которые в данном опыте которые в данном опыте происходят или не происходят, можно выделить совокупность так называемых элементарных событий, обладающих следующими свойствами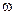 , а их совокупность- буквой
, а их совокупность- буквой 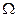 и называют пространством элементарных событий.
и называют пространством элементарных событий.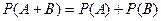 .
. образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
образуют полную группу несовместных событий, то сумма их вероятностей равна единице: .
. .
. .
. , вычисленная при условии, что имело место событие А, называется условной вероятностью события В:
, вычисленная при условии, что имело место событие А, называется условной вероятностью события В: или
или  .
. или
или  .
.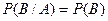 , и теорема умножения вероятностей принимает вид:
, и теорема умножения вероятностей принимает вид: .
. .
. .
. , а
, а 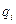 – вероятность противоположных событий
– вероятность противоположных событий  .
. .
. . Эта вероятность равна 1 – 0,875 = 0,125, т.е. в цель не попадают ни одного раза.
. Эта вероятность равна 1 – 0,875 = 0,125, т.е. в цель не попадают ни одного раза.
 что не белый -
что не белый - 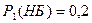 . Вероятность того, что взятый из второй коробки шар белый -
. Вероятность того, что взятый из второй коробки шар белый - 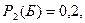 что не белый -
что не белый -  Вероятность того, что повторно выбран шар, извлеченный из первой коробки и вероятность того, что повторно выбран шар, извлеченный из второй коробки, равны 0,5. Вероятность того, что повторно выбран шар, извлеченный из первой коробки, и он белый -
Вероятность того, что повторно выбран шар, извлеченный из первой коробки и вероятность того, что повторно выбран шар, извлеченный из второй коробки, равны 0,5. Вероятность того, что повторно выбран шар, извлеченный из первой коробки, и он белый - 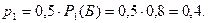 Вероятность того, что повторно выбран шар, извлеченный из второй коробки, и он белый -
Вероятность того, что повторно выбран шар, извлеченный из второй коробки, и он белый -  Вероятность того, что повторно будет выбран белый шар, равна
Вероятность того, что повторно будет выбран белый шар, равна 
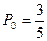 , а вероятность того, что выбрана винтовка без оптического прицела, обозначим
, а вероятность того, что выбрана винтовка без оптического прицела, обозначим  . Вероятность того, что выбрали винтовку с оптическим прицелом, и при этом цель была поражена
. Вероятность того, что выбрали винтовку с оптическим прицелом, и при этом цель была поражена  , где
, где  – вероятность поражения цели из винтовки с оптическим прицелом.
– вероятность поражения цели из винтовки с оптическим прицелом. , где
, где  – вероятность поражения цели из винтовки без оптического прицела.
– вероятность поражения цели из винтовки без оптического прицела. и
и  , т.к. для поражения цели достаточно, чтобы произошло одно из этих несовместных событий.
, т.к. для поражения цели достаточно, чтобы произошло одно из этих несовместных событий. .
. ;
;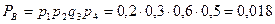 ;
; ;
; .
.
 .
. ). Т.к. после успешного ответа на первый вопрос остается еще 39 вопросов, на 34 из которых ответы известны:
). Т.к. после успешного ответа на первый вопрос остается еще 39 вопросов, на 34 из которых ответы известны:  .
. ), на третий – ответили (вероятность
), на третий – ответили (вероятность  ):
):  .
. ), на второй – ответили (вероятность
), на второй – ответили (вероятность  ), на третий–ответили (вероятность
), на третий–ответили (вероятность  .
. .
. , для второй детали, извлеченной из первой партии при условии, что первая деталь была не бракованной -
, для второй детали, извлеченной из первой партии при условии, что первая деталь была не бракованной -  .
. , для второй детали, извлеченной из второй партии при условии, что первая деталь была не бракованной -
, для второй детали, извлеченной из второй партии при условии, что первая деталь была не бракованной -  .
. .
. ) и при этом она – бракованная (вероятность -
) и при этом она – бракованная (вероятность -  ). Окончательно:
). Окончательно: 
 ) и при этом она – бракованная (вероятность -
) и при этом она – бракованная (вероятность - 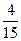 ). Окончательно:
). Окончательно: 
 .
. ), а второй – черный (вероятность -
), а второй – черный (вероятность -  ).
). ), а второй – белый (вероятность -
), а второй – белый (вероятность -  ).
).
 , при вытаскивании второй карты -
, при вытаскивании второй карты -  , третьей -
, третьей - 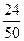 , четвертой -
, четвертой -  . Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна
. Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна  . Следовательно,
. Следовательно, 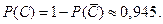
 . Вероятность того, что не выпадет 6 очков -
. Вероятность того, что не выпадет 6 очков -  . Вероятность того, что при броске трех костей не выпадет ни разу 6 очков, равна
. Вероятность того, что при броске трех костей не выпадет ни разу 6 очков, равна  .
. .
. ; вероятность осечки -
; вероятность осечки - 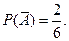 Вероятность выстрела при втором нажатии на курок зависит от результата первого нажатия.
Вероятность выстрела при втором нажатии на курок зависит от результата первого нажатия. если в первый раз был выстрел,
если в первый раз был выстрел,  - если в первый раз произошла осечка.
- если в первый раз произошла осечка. , если в первый раз произошел выстрел,
, если в первый раз произошел выстрел,  - если в первый раз была осечка.
- если в первый раз была осечка. ) при условии, что в первом случае произошел выстрел (событие А) или осечка (событие
) при условии, что в первом случае произошел выстрел (событие А) или осечка (событие  - два выстрела подряд;
- два выстрела подряд; - первая осечка, второй выстрел;
- первая осечка, второй выстрел;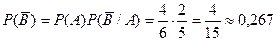 - первый выстрел, вторая осечка;
- первый выстрел, вторая осечка; - две осечки подряд.
- две осечки подряд. .
. Условные вероятности второго выстрела и осечки вычисляются из условия, что напротив ствола может оказаться то же гнездо, что и в первый раз.
Условные вероятности второго выстрела и осечки вычисляются из условия, что напротив ствола может оказаться то же гнездо, что и в первый раз. если в первый раз был выстрел,
если в первый раз был выстрел,  - если в первый раз произошла осечка.
- если в первый раз произошла осечка. , если в первый раз произошел выстрел,
, если в первый раз произошел выстрел, 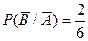 - если была осечка.
- если была осечка. - два выстрела подряд;
- два выстрела подряд; - первая осечка, второй выстрел;
- первая осечка, второй выстрел;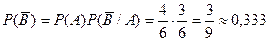 - первый выстрел, вторая осечка;
- первый выстрел, вторая осечка;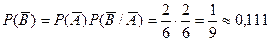 - две осечки подряд.
- две осечки подряд.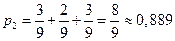 .
.
 .
. .
. .
.


 .
. .
.
 .
. ;
;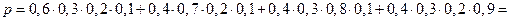
 ;
;  .
. ;
;  .
.
 , составляющих полную группу событий. Пусть известны вероятности этих событий
, составляющих полную группу событий. Пусть известны вероятности этих событий  и условные вероятности наступления события А при наступлении события
и условные вероятности наступления события А при наступлении события 
 :
:  .
.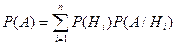 .
. .
. также несовместны. Тогда можно применить теорему о сложении вероятностей несовместных событий:
также несовместны. Тогда можно применить теорему о сложении вероятностей несовместных событий: .
. . Окончательно получаем:
. Окончательно получаем:  Теорема доказана.
Теорема доказана. - нормальный режим работы прибора,
- нормальный режим работы прибора,  - ненормальный, событие А - выход из строя прибора. По условиям задачи:
- ненормальный, событие А - выход из строя прибора. По условиям задачи: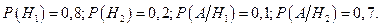

 имеет дефект. В цехе три контролёра; изделие осматривает только один контролёр (с одинаковой вероятностью первый, второй или третий). Вероятность обнаружения дефекта (если он имеется) для
имеет дефект. В цехе три контролёра; изделие осматривает только один контролёр (с одинаковой вероятностью первый, второй или третий). Вероятность обнаружения дефекта (если он имеется) для  - го контролёра равна
- го контролёра равна 
 . Если изделие не было забраковано в цехе, оно попадёт в ОТК завода, где дефект, если он имеется, обнаруживается с вероятностью
. Если изделие не было забраковано в цехе, оно попадёт в ОТК завода, где дефект, если он имеется, обнаруживается с вероятностью  . Определить вероятность следующих событий:
. Определить вероятность следующих событий:
 .
.
 - дефект имеется и его обнаруживает первый контролёр,
- дефект имеется и его обнаруживает первый контролёр,  - то же, - второй контролёр,
- то же, - второй контролёр,  - то же, - третий;
- то же, - третий; 


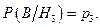 Следовательно, по формуле полной вероятности:
Следовательно, по формуле полной вероятности: 


 .
. (так как после перекладывания в первой партии осталось 9 деталей и не осталось бракованных);
(так как после перекладывания в первой партии осталось 9 деталей и не осталось бракованных);  (осталось 9 деталей, среди которых одна бракованная).
(осталось 9 деталей, среди которых одна бракованная).  (так как во второй партии после перекладывания бракованной детали оказалось 13 деталей, из которых 2 бракованных). Аналогично, находим
(так как во второй партии после перекладывания бракованной детали оказалось 13 деталей, из которых 2 бракованных). Аналогично, находим 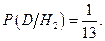 Тогда по формулам полной вероятности получим
Тогда по формулам полной вероятности получим