
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства математического ожиданияСодержание книги
Поиск на нашем сайте 1) Математическое ожидание постоянной величины равно самой этой постоянной:
2) Постоянный множитель можно выносить за знак математического ожидания:
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
Это свойство справедливо для произвольного числа случайных величин. 4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
Это свойство также справедливо для произвольного числа случайных величин. Пусть производится п независимых испытаний, вероятность появления события А в которых равна р. Теорема. Математическое ожидание
Дисперсия случайной величины
Определение. Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Пример. Для рассмотренного выше примера находим. Математическое ожидание случайной величины равно:
Возможные значения квадрата отклонения:
Дисперсия равна:
Однако, на практике подобный способ вычисления дисперсии неудобен, т.к. приводит при большом количестве значений случайной величины к громоздким вычислениям. Поэтому применяется другой способ.
Вычисление дисперсии
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:
Доказательство. С учетом того, что математическое ожидание
Применим эту формулу для рассмотренного выше примера:
Свойства дисперсии
1) Дисперсия постоянной величины равна нулю:
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин:
Справедливость этого равенства вытекает из свойства 2. Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность появления события постоянна, равна произведению числа испытаний на вероятности появления
Пример. Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта. Наугад выбирают 1000 изделий. Пусть Х – число изделий первого сорта в данной выборке. Найти закон распределения, математическое ожидание и дисперсию случайной величины. Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна р = 0,96. Таким образом, закон распределения может считаться биноминальным.
Пример. Найти дисперсию дискретной случайной величины Х – числа появлений события А в двух независимых испытаниях, если вероятности появления этого события в каждом испытании равны и известно, что Т.к. случайная величина Х распределена по биноминальному закону, то
Пример. Производятся независимые испытания с одинаковой вероятностью появления события А в каждом испытании. Найти вероятность появления события А, если дисперсия числа появлений события в трех независимых испытаниях равна 0,63. По формуле дисперсии биноминального закона получаем:
Пример. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно Принимая за случайную величину число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3 или 4. Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем 1) Не отказал ни один прибор:
2) Отказал один из приборов:
3) Отказали два прибора:
4) Отказали три прибора:
5) Отказали все приборы:
Получаем закон распределения:
Математическое ожидание:
Дисперсия:
Определение. Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии:
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

 .
. .
. .
.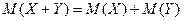 .
. числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: .
. .
.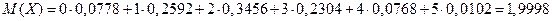 .
. ;
;  ;
; ;
; 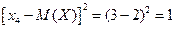 ;
; ;
;  .
. .
. .
.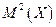 – величины постоянные, можно записать:
– величины постоянные, можно записать:

 ;
;
 .
. .
. .
. .
. и вероятность
и вероятность  непоявления события в каждом испытании:
непоявления события в каждом испытании: .
.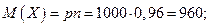





 ;
;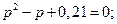

 ;
; 
 ;
; 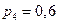 . Найти математическое ожидание и дисперсию числа отказавших приборов.
. Найти математическое ожидание и дисперсию числа отказавших приборов. .
.
 0,302.
0,302.

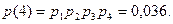






 .
. .
.


