
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пространство элементарных событий. Классическое определение вероятностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пространство элементарных событий. Классическое определение вероятности w-возможные исходы опыта G называются элементарными событиями, если их нельзя разложить на составляющие их события. Эти события взаимоисключающие и в результате ровно 1 из них точно произойдет. Сов-ть всех элементарных событий w данного опыта G называется пространством элементарных событий Ω Классической схемой называется опыт G, при котором кол-во элементарных исходов конечно и все они равновозможны. Благоприятное – если наступление w ведет к наступлению А. Вероятность- отношение числа m элементарных событий к числу n всех элементарных событий в этой схеме..
4. Геометрическая вероятность. Задача о встрече В случае бесконечного кол-ва равновозможных элементарных исходов опыта Gпространство элементарных событий можно представить в виде некоторого множества Ω в пространстве RПри этом элементарные исходы есть точки заполняющие мн-во Ω, тогда любому событию А соответствует некоторое подмножество мн-ва Ω. Вер-ть(геометр) – называется отношение меры мн-ва А к мере мн-ва Ω(в виде квадрата ед.площади) Р(А)=S(A)=V(A) Задача о встрече: 2 студента договорились встретиться. Каждый из них приходит в течение 1 ч. и ждет 20 мин. Какова вероят. их встречи? Опишем пр-во эл. соб.: Пусть x- время прихода 1 студ., y- время прихода 2-го студ. Тогда 0≤x≤1ч. и 0≤y≤1ч.; в кач-ве Ω м. рассматривать квадрат. Событие А={студ.встретятся}={|x-y|<1/3} |x-y|<1/3 ‹=› -1\3<x-y<1\3 y=x+1/3 y=x-1/3 P(A)=S(A)/S (Ω)=1-2\3*2\3=5\9
Действия над событиями. Диаграммы Венна. Пусть некоторому опыту G соот-т простр-во элем-ых событий Ω, кот. изображ-ся в виде квадрата един-й площади. Вводимые далее действия над событиями м/представить также как операции над множ-ми и проиллюстр-ть с помощью диаграмм Венна. Будем говорить, что соб. А влечет за собой соб.В, если из наступления А следует наступление В.( Суммой(объединением) соб.А и В наз. такое соб. С, кот. происходит т. и т.т., когда происх-т по крайне мере 1 из соб-й А и В.( Разностью соб. А и В наз. соб. С, кот. происходит т. и т.т., когда А происх-т, а В не происх-т.(С=А-В; С=А\В) Произведением (пересечением) соб.А и В наз. С, кот. происходит т. и т.т., когда происходит А и В. (С=А*В; С=А∩В) Соб. А и В наз. несовместными (не пересекающимися), если они не могут произойти одновременно, т.е. А*В=ǿ Соб. В наз. противоположным к соб.А (дополнительным к А)[В= Ă], если оно происходит т. и т.т., когда А не происходит.(В=Ă)В рез-те опыта G 1 из 2-х соб-й А и Ă обязательно произойдет и эти события не совместны.(А+Ă= Ω; А*Ă= ǿ) Говорят, что соб-я образуют полную группу(попарно несовместных) событий если: а)в рез-те G одно из них обязательно произойдет
Теорема сложения вероятностей. Вер-ть разности двух событий Пусть нек-ому опыту G соотв-т простр-во элемент-ых соб. Ω;, кот-ое будем изобр-ть в виде квадрата единичной площади. P(A)=S(A). 1. Теорема сложения вер-ей Вер-ть суммы 2-х соб. равна сумме вер-ей этих соб. без вер-ти их произведения. P(A+B)=P(A)+P(B)-P(AB) Следствие: 1)для несовместных событий: P(A+B)=P(A)+P(B); 2)для полной группы соб. H1,+,Hn: P(H1+…+Hn)=P(Ω)=1 3)сумма вер-ей противополож. соб. Равна 1: P(A)+P(Ā)=1; P(A)=1-P(A) 2. Вероятность разности 2-х соб. P(A-B)=P(A)-P(AB)
7.Вероятность противоположного события. Связь между вер-ми событий из полной группы
Формула Байеса пусть события Hi,i=1,nобразуют полную группу событий (Р(Нi)>0). И если событие А произошло, то вероятности гипотез Hi,i=1,n вычисляются по формуле Байеса
Где Р(А), вероятность события А, вычисленная по формуле полной вероятности.
Функция распределения СВ и ее свойства Функцией распределения случайной величины Х называется функция FX(x)= P{X<x}, xÎR Под {X<x}понимается событие, состоящее в том, что случайная величина Х принимает значение меньшее, чем число х Свойства: 1)для любого xÎR: 0£ F(x) £ 1 2) F(-¥) = limx®¥ F(x) = 0; F(+¥) = limx®¥ F(x) = 1; 3) F(x)-неубывающаяфункция, т.е.длялюбыхα,βтаких, чтоα<β:F(β) - F(α); 4)непрерывна слева Х0
20. Функция распределения ДСВ Пусть ДСВ задана табл. распред-ем, тогда ее ф-ция распределения:
где x1<x2<…<xn<x
Графиком ф-ции распред-я д/ДСВ явл-ся кусочно-постоянная ф-ция. Св-ва ф-ции распред-я: 1.) монотонно не убывает; 2.) непрерывна слева; 3.) limF(x)=0, limF(x)=1 x→-∞ x→+∞
Неравенства Маркова. Теорема: Пусть Св Х принимает только неограниченное значение α- любое положительное число тогда вероятность того что СВ х≥0 ¥ α>0 P(x<α)≥1- Док-во т к х≥0
M(X)= P(X≥α)≤M(X)/α -P(X≥α)≥-M(X)/α 1-p(X≥α)≥1-M(X)/α
Неравенства Чебышева. Если Х-СВ, мат. ожидание к-рой М(Х) = а, а дисперсия D(Х) конечна, то д/любого числа ε> 0 выполняются неравенства:
Док-во Ιx-M(X)ι<E↔(X-M(X))2<E2 Введем новую СВ Y=(X-M(X))2≥0 M(X)=M(X_M(X))2=D(X) P(X)<E2)≥1-M(X)/E2=1-D(X)/E2т к события РΙx-M(X)ι≥E противоположные то справедливо неравенство РΙx-M(X)ι≥E)≤D(X)/E2 При неизв-ом з-не распред-я на практике при известных М(Х),D(X) участком возможных значений СВ Х считают М(Х)±3σ(Х)
Теорема Бернулли. Если вероятность наступления событ А в каждом изn -_независ испыт постоянно то при неограниченном увеличении числа n –испытаний относит частота m/n –наступления событияА стремиться по вероятности к числу р т е для любого Е>0
Док-во Рассм Св Х1,Х2…..Хn где Xi–число наступлений события А в i- ом испытании хi 0 1.
рi 1-р р.
M(X)=p D(X)=pq=c
Пространство элементарных событий. Классическое определение вероятности w-возможные исходы опыта G называются элементарными событиями, если их нельзя разложить на составляющие их события. Эти события взаимоисключающие и в результате ровно 1 из них точно произойдет. Сов-ть всех элементарных событий w данного опыта G называется пространством элементарных событий Ω Классической схемой называется опыт G, при котором кол-во элементарных исходов конечно и все они равновозможны. Благоприятное – если наступление w ведет к наступлению А. Вероятность- отношение числа m элементарных событий к числу n всех элементарных событий в этой схеме..
4. Геометрическая вероятность. Задача о встрече В случае бесконечного кол-ва равновозможных элементарных исходов опыта Gпространство элементарных событий можно представить в виде некоторого множества Ω в пространстве RПри этом элементарные исходы есть точки заполняющие мн-во Ω, тогда любому событию А соответствует некоторое подмножество мн-ва Ω. Вер-ть(геометр) – называется отношение меры мн-ва А к мере мн-ва Ω(в виде квадрата ед.площади) Р(А)=S(A)=V(A) Задача о встрече: 2 студента договорились встретиться. Каждый из них приходит в течение 1 ч. и ждет 20 мин. Какова вероят. их встречи? Опишем пр-во эл. соб.: Пусть x- время прихода 1 студ., y- время прихода 2-го студ. Тогда 0≤x≤1ч. и 0≤y≤1ч.; в кач-ве Ω м. рассматривать квадрат. Событие А={студ.встретятся}={|x-y|<1/3} |x-y|<1/3 ‹=› -1\3<x-y<1\3 y=x+1/3 y=x-1/3 P(A)=S(A)/S (Ω)=1-2\3*2\3=5\9
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1073; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.223.136 (0.008 с.) |


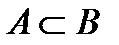 ;
;  )
) )
) ; б) любые 2 из них не м/произойти одновр-но(
; б) любые 2 из них не м/произойти одновр-но( ¢
¢

 R
R


 (1)
(1)



 <E)=1
<E)=1


