Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о центральной предельной теореме.Содержание книги
Поиск на нашем сайте Закон больших чисел устанавливает факт приближения большого кол-ва СВ к определенным постоянным однако суммарные действия СВ не ограничивается только такими закономерностями Оказывается что совокупные действия многих случ факторов СВ приводит к определнному закону распределения а именно к норм закону распред Теорема Ляпунова Пусть Xi…Xn–независ Св имеющие матем ожидание M(Xi)=aibD(X)= M= Т к для Св выполн все условия теоремы Чебышева то мы можем записать для них неравенство с cc-pq P(ǀ P(ǀm/n-np/nǀ)<E)≥1-pq/nE2
36.Генеральная и выборочная совокупности. Дискретный вариационный ряд и его графические изображения. Мат. Ст-ка занимается установлением закономерностей, к-рым подчинены массовые случайные явления, на основе обработки стат. данных, полученных в результате наблюдений. Генеральная совокупность – все множество имеющихся объектов. Выборка – набор объектов, случайно отобранных из генеральной совокупности. Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности. Виды выборки: повторная и бесповторная. Выборка должна правиль-но представлять пропорции ген.сов-сти, то есть быть репрезентативной (представительной). Учитывая закон больших чисел, можно утверждать, что это условие выполняется, если каждый объект выбран случайно, причем д/любого объекта вероятность попасть в выборку одинакова. Вариационный ряд наз-ся ряд вариант расположенных в порядке возрастания вместе с соответствующими весами если изуч.ДСВ то ДВР. Полигон –ломаная соединяющая точки плоскости с координатами (х,mi) Кумулянта- ломаная соед точки плос-ти с корд-ми(x,mxi) Гистограмма –для изобр.вар.рядов и имеют вид ступ фигурыиз прямоуг.с основ.=длина инт-ла и высотами=частотам.
37.Интервальный вариационный ряд и его графические изображения. Интервальный ряд –ряд, представляющий собой выборку непрерывной случ велечины. Для построения интер. Вар. Ряда разбивают множество значений вариант на полуинтервалы [ак, ак=1], т.е. проводят группировку. Для определения оптим. велечины интервала используют формулу Стерджерса: h=(xmax-xmin)/(1+3,332ln n). Для графического представления интер.вар. ряда используется гистрограмма – ступенчатая фигура, состоящая из прямоугольников, основанием для которых служат частичные интервалы, а высоты – частоты или частости.
Эмперическая функция и эмперическая плотность распределения. Эмп. ф-цией распределения – ф-ция, значения которой в точке х равно накопленной частоте, т.е. Fn(x)=wx=mx/n Для интервального ряда указываются не конкретные значения вариант, а только их частоты на интервалах. В этом случае эмпирич. ф-я распределения определена только на концах интервалов. Ее можно изобразить ломаной, проходящей через точки (ai,Fn(ai)), i= Эмпирическая плотность распр-я непрерывного вар. ряда – ф-я
Ф-я fn является аналогом плотности распределения случайной величины(площадь области под графиком равна
Основные числовые характеристики вариационных рядов. Среднее арифметическое и выборочная дисперсия и их свойства. Средняя арифметическая (выборочное среднее): для дискретного выборочного ряда:
для интервального ряда Свойства средней арифметической: 1)если xi = с, то 3) Вариационный размах R: R=xmax-xmin. Ср. лин. отклонение d = Выборочная дисперсия - мера рассеивания-средняя арифметическая квадратов отклонений вариант от их выборочной средней: S2= Св-ва выборочной дисперсии:1)Дисперсия постоянной равна нулю;2)Если ко всем вариантам добавить постоянное число, то дисперсия не изменится;3)Если все варианты умножить на одно и то же число k, то дисперсия умножится на k2;
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.181.14 (0.006 с.) |

 и абсолютные центральные моменты 3-го порядка
и абсолютные центральные моменты 3-го порядка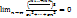 тогда закон распред суммы Yn=X1….+Xn неограниченно приближается к норм закону с ростом n с мат ожиданием N(
тогда закон распред суммы Yn=X1….+Xn неограниченно приближается к норм закону с ростом n с мат ожиданием N( 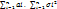 )
)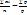 ǀ<E)≥1-pq/nE2
ǀ<E)≥1-pq/nE2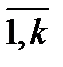
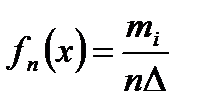 , если ai ≤ x≤ ai+1, i=
, если ai ≤ x≤ ai+1, i= 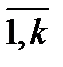 ; или =0, если x<a или x>ak+1.
; или =0, если x<a или x>ak+1.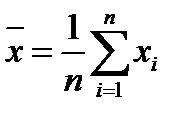 ,
,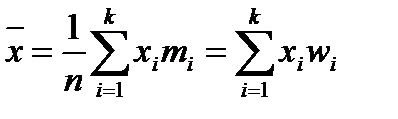 , где xi - середина i-го интервала.
, где xi - середина i-го интервала.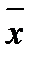 = с; 2)
= с; 2) 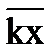 = k
= k 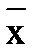 ;
;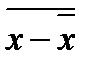 = 0; 4)
= 0; 4) 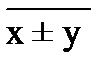 =
= 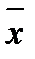 ±
± 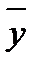 ;
;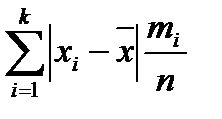 .
.