Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аксиоматическое определение вероятностиСодержание книги
Поиск на нашем сайте
Вероятность события в современном построении курса определяется аксиоматически (аксиоматическая структура теории вероятностей была предложена советским математиком А. Н. Колмогоровым в 1933 году). Дадим это определение в упрощенной трактовке. Пусть Аксиома 1: Аксиома 2: вероятность достоверного события Аксиома 3: если
В аксиоматическом определении свойства вероятности, справедливые для испытаний с равновозможными исходами, обобщены на случай произвольных испытаний. Эти свойства, в общем случае, ниоткуда не следуют, они постулируются. Именно так, с помощью некоторого набора аксиом, определяются исходные понятия в современной математике. Можно показать, что «классическое определение» вероятности (3.4) получается как частный случай аксиоматического определения, если исходы испытания равновероятны, Без доказательства приведем несколько следствий из аксиом 1–3: 1. 2. Если 3. 4. Если исходы 5. Статистическое определение вероятности Лишь в случае испытаний с равновозможными исходами мы можем каждому исходу приписать определенную вероятность, как это делалось в разделе 3.3. В общем случае с помощью аксиоматического определения вероятности нельзя найти численные значения вероятностей событий в реальных испытаниях. Каким же образом формальное аксиоматическое определение вероятности связано с действительностью? Такая связь основана на универсальной закономерности природы, составляющей суть так называемого «статистического определения вероятности». Пусть производится серия однотипных реальных испытаний, в каждом из которых может наступить (или не наступить) событие А. Относительной частотой события А является величина Пример 3.14 Партия, содержащая 100 деталей, подвергается контролю. 10 деталей оказались бракованными. Относительная частота события Очевидно, относительная частота может меняться от серии к серии. В то же время экспериментально установлен очень важный факт: при осуществлении известных условий с ростом Фундаментальное свойство устойчивости относительных частот позволяет установить связь теории вероятностей – математической дисциплины – с многочисленными практическими приложениями. Благодаря этому свойству оказалось возможным приписывать событиям определенные вероятности, значения которых находятся экспериментально. Как показывает опыт, для классических испытаний с равновозможными исходами относительная частота
Условная вероятность В реальности вероятность какого-либо события Пример 3.15 Студент, из 30 билетов выучил первые 20. На экзамен он пришел одним из последних, когда осталось только 8 билетов с 17-го по 24-й (событие Если, придя на экзамен, студент не получил никакой информации об оставшихся билетах, то по классическому определению = 4/8 =1/2. Можно показать, что для классического испытания с равновозможными исходами имеет место формула
Формула (3.6) принимается за определение условной вероятности и в общем случае. Можно показать, что величина
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.222 (0.005 с.) |

 т. е. событие
т. е. событие  образовано из каких-нибудь исходов пространства элементарных событий некоторого испытания. Числовая функция
образовано из каких-нибудь исходов пространства элементарных событий некоторого испытания. Числовая функция  , определенная на множестве всех событий этого испытания, называется вероятностью события
, определенная на множестве всех событий этого испытания, называется вероятностью события  .
. .
. попарно несовместные события, то
попарно несовместные события, то – вероятность суммы несовместных событий равна сумме вероятностей этих событий.
– вероятность суммы несовместных событий равна сумме вероятностей этих событий. , (
, ( – невозможное событие).
– невозможное событие). , то
, то  .
. , (вместе с аксиомой 1 имеем
, (вместе с аксиомой 1 имеем 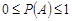 ).
). ,
, 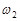 , …,
, …,  образуют пространство элементарных событий, то
образуют пространство элементарных событий, то  .
. .
. , где т – число испытаний, в которых событие
, где т – число испытаний, в которых событие  – общее число испытаний в серии.
– общее число испытаний в серии.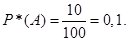
 с некоторого момента начинает колебаться около определенного числа, все меньше от него отклоняясь. Это число называют вероятностью события
с некоторого момента начинает колебаться около определенного числа, все меньше от него отклоняясь. Это число называют вероятностью события 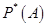 , устанавливаемая эмпирически при большом числе повторений, и вероятность
, устанавливаемая эмпирически при большом числе повторений, и вероятность 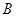 ,
,  ,..., т.е. зависит от некоторых условий. Вероятность события
,..., т.е. зависит от некоторых условий. Вероятность события  (или
(или  ).
). . Если же он узнал, что событие
. Если же он узнал, что событие  =
=