Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики случайных величинСодержание книги
Поиск на нашем сайте
Математическим ожиданием случайной величины X (обозначается
Вероятностный смысл математического ожидания ДСВ – это число, около которого группируются средние значения случайной величины с ростом числа испытаний. Математическое ожидание непрерывной случайной величины вычисляется по формуле
Пример 3.21. Пусть распределение ДСВ задано таблицей: Таблица 3.1
Найти математическое ожидание Решение
Пример 3.22. Пусть распределение НСВ задано плотностью вероятности (3.24):
Найти математическое ожидание Решение
Дисперсия и среднее квадратическое отклонение Обозначение дисперсии
Для ДСВ это означает (см. (2.7))
для НСВ (см. (2.8)):
Дисперсия характеризует рассеивание случайной величины относительно ее математического ожидания. Формулы (3.30) и (3.31) можно преобразовать к более удобному для вычислений виду
Пример 3.22 Найдем дисперсию ДСВ по табл. 4: Пример 3.23 Найдем дисперсию НСВ, заданной плотностью вероятности (3.28):
Чаще рассеивание характеризуют средним квадратическим отклонением – величиной, имеющей ту же размерность, что и сама случайная величина X:
В примере 3.22 Свойства дисперсии: 1) 2) 3)
Другие числовые характеристики Случайной величины 1. Мода (Мо). Модой ДСВ называется ее наивероятнейшее значение. Например, по таблице 2.4: Мо = 1. Модой НСВ называется значение Х = Мо, соответствующее максимуму плотности вероятности 2. Квантили. Число Так как Таким образом,
(см. свойство 3 плотности вероятности в подразделе 2.5). Квантили Пример 2.14. Найдем 25-й процентиль
(отрицательный корень отбрасываем, так как в интервал 7. Медиана (Ме). Медианой называется половинный квантиль: Ме = Например, для распределения (2.1) имеем;
(найдите на графике к примеру 2.4 точки Биномиальное распределение (распределение Бернулли) Пусть производится n независимых испытаний, в каждом из которых событие
Здесь По формуле (3.36) можно найти вероятность того, что событие Пример 3.24. Производится 4 выстрела по мишени с вероятностью попадания 0,8 в каждом выстреле. Найти вероятность 1) ровно двух попаданий, 2) ровно трех попаданий.
Решение 1. 2. Заметим, что события (k = 0), (k = 1),... (k = n) несовместны и в сумме образуют достоверное событие Основные числовые характеристики биномиального распределения вычисляются по формулам
В примере 2.15 Мода (наивероятнейшее значение) биномиального распределения
При этом, если
Пример 3.25 Найти наивероятнейшее число попаданий при четырех выстрелах в примере 1.1.
Решение. При этом вероятности 3 и 4 попаданий одинаковы:
3.19. Нормальное распределение (закон Гаусса) Нормальное распределение задается плотностью вероятности
Можно показать, что функция Кривая
Рис. 3.1. Параметры Кривая нормального распределения Введем функцию Лапласа
Таблица значений функции 1) 2) 3) 4) 5) Функция распределения для нормального закона находится через функцию Лапласа (2.21) по формуле
С помощью функции Лапласа находится вероятность попадания нормально распределенной случайной величины в заданный интервал:
Для интервала, симметричного относительно математического ожидания, формула (2.23) дает следующее:
или
Если в формуле (2.24) положить
все (99,73%) значения нормально распределенной величины попадают в интервал Нормальный закон встречается чаще всего в приложениях теории вероятностей. Им с большой моделируются реальные.распределения размеров и веса изделий в одной партии, отклонения точек попадания снаряда от цели, ошибки измерений, распределение людей по росту, по интеллектуальным возможностям и т. д. Пример 1.3 Шарики для подшипников отбраковываются так: если они проходят в отверстие диаметром Решение. Диаметр шарика – случайная величина Х, распределенная по нормальному закону с математическим, ожиданием
Таким образом, при назначенном допуске 95% изготовленных шариков окажутся стандартными. Пример 3.4 Случайная величина X распределена по нормальному закону с математическим ожиданием тх = 8и средним квадратическим отклонением Решение По формуле (2.23) имеем
ТРЕНИРОВОЧНЫЙ ТЕСТ По закону распределения
в задачах 1– 5 найдите следующее.
По функции распределения
найдите:
Ответы: 1В, 2А, 3Д, 4Б, 5В, 6Б, 7Г, 8Б, 9Г; 10А; 11Г; 12Б, 13Д, 14В, 15Д.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.132.43 (0.011 с.) |

 или
или  )называется величина
)называется величина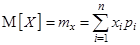
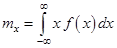 .
.

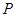
 .
. .
.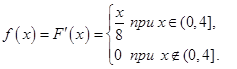
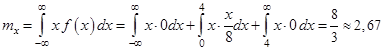
 или
или  .По определению,
.По определению,
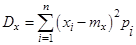



 – (1,1) 2 = 1,99.
– (1,1) 2 = 1,99. .
.
 , в примере 3.28
, в примере 3.28  .
.

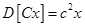 .
. . Для случайной величины в примере 2.4 Мо=4.
. Для случайной величины в примере 2.4 Мо=4. называется р - м квантилем распределения, если оно удовлетворяет уравнению
называется р - м квантилем распределения, если оно удовлетворяет уравнению  , где
, где 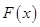 –функция распределения (см. (2.3)).
–функция распределения (см. (2.3)). ,
,  , то
, то  .
. – это точка, левее которой случайная величина попадает с вероятностью р. Для НСВ квантиль Кр может быть найден из уравнения
– это точка, левее которой случайная величина попадает с вероятностью р. Для НСВ квантиль Кр может быть найден из уравнения
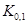 ,
, 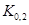 ,...,
,...,  называются децилями. Квантили
называются децилями. Квантили  ,
, 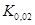 ,...,
,..., 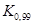 называются процентилями.
называются процентилями.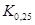 распределения (2.5). По определению
распределения (2.5). По определению 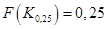 или из (2.20):
или из (2.20):

 .
.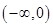 случайная величина X не попадает).
случайная величина X не попадает). . Очевидно, значения случайной величины X с одинаковой вероятностью 0,5 могут оказаться как левее, так и правее точки X =Ме.
. Очевидно, значения случайной величины X с одинаковой вероятностью 0,5 могут оказаться как левее, так и правее точки X =Ме.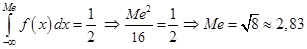
 .
. появляется с одной и той же вероятностью р. Такая ситуация называется схемой Бернулли. Требуется найти вероятность того, что событие
появляется с одной и той же вероятностью р. Такая ситуация называется схемой Бернулли. Требуется найти вероятность того, что событие  и находится по формуле Бернулли
и находится по формуле Бернулли
 ,
,  – число сочетаний из n элементов по k.
– число сочетаний из n элементов по k.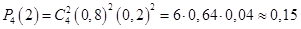 ,
, .
. =1.
=1.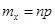 ,
,  ,
, 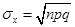
 ;
;  ;
;  .
.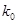 находится из неравенства
находится из неравенства
 есть целое число, то биномиальное распределение имеет две моды:
есть целое число, то биномиальное распределение имеет две моды: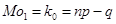 и
и  .
.

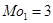 ,
,  .
. .
.
 = 1.
= 1. имеет вид, изображенный на рис. 3.1.
имеет вид, изображенный на рис. 3.1.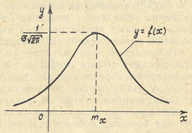
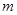 и
и  в формуле (2.20) являются соответственно математическим ожиданием (
в формуле (2.20) являются соответственно математическим ожиданием ( ) и средним квадратическим отклонением (
) и средним квадратическим отклонением ( ) нормально распределенной случайной величины
) нормально распределенной случайной величины  , поэтому
, поэтому 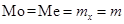 .
.
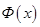 приведена в прилож. 2. Свойства функции Лапласа
приведена в прилож. 2. Свойства функции Лапласа , т.е.
, т.е.  ;
; ;
; , если
, если  ;
;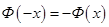 , т.е.
, т.е. 



 , то получим
, то получим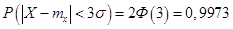
 . Этот факт называют «правилом трех сигм». Интервал I называется зоной практического рассеивания.
. Этот факт называют «правилом трех сигм». Интервал I называется зоной практического рассеивания. , но не проходят в отверстие диаметром
, но не проходят в отверстие диаметром  , то признаются стандартными. Пусть допуск, т. е. интервал
, то признаются стандартными. Пусть допуск, т. е. интервал  , составляет 2/3 зоны практического рассеивания. Требуется предсказать долю шариков, прошедших отбраковку.
, составляет 2/3 зоны практического рассеивания. Требуется предсказать долю шариков, прошедших отбраковку.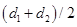 и средним квадратическим отклонением
и средним квадратическим отклонением  . По формуле (3.24) находим
. По формуле (3.24) находим .
. . Найти P (5<Х<9).
. Найти P (5<Х<9).
 ; Б)
; Б)  ; В)
; В) 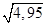 ; Г)
; Г)  ;
Д)
;
Д) 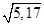 .
.
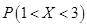
 2)
2)  3)
3)  .
.
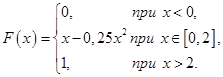


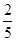 ; Б)
; Б)  ; В) 0;
Г)
; В) 0;
Г)  ; Д) 0.
; Д) 0.
 ; Б)
; Б)  ; В)
; В)  ;
Г)
;
Г)  ; Д)
; Д) 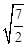 .
.
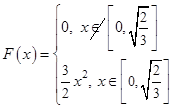 Найти медиану.
Найти медиану.
 ; Б)
; Б)  ;
Г)
;
Г)  ; Д)
; Д)  .
.