
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция №2 Вероятность событийСодержание книги
Поиск на нашем сайте
Теория вероятности Лекция№1 Случайные события Опр1: опыт, эксперимент, наблюдение явления будем называть испытанием. Опр2: произвольное множества Ω (омега) называем пространством элементарных событий, а элементы ω (омега) этого множества будем называть элементарными событиями (элементарными исходами). Замечание: элементарным событием соответствует взаимоисключающие исходы опыта (испытания). Опр3: произвольное подмножество пространство элементарных событий называется случайным событием или просто событием. Обозначают: А, В, С… Опр4: говорят, что в результате испытания осуществилось (наступило) событие А, если произошло элементарное событие ω Є А. Операции над событиями Опр5: суммой событий А и В называется событие С, состоящее из всех элементарных событий, которые входят или в событие А или в событие В или в то и другое. Обозначают: С = А + В или С = A U В. Замечание: событие А + В состоит в том, что произошло по крайней мере одно из двух событий А или В. Опр6: произведением событий А и В называется событие С, состоящее из всех элементов, которые одновременно входят в обои события А и В. Обозначают: С = АВ или С = А ∩ В. Замечание: событие АВ происходит тогда и только тогда, когда происходят одновременно и событие А, и событие В. Опр7: разностью событий А и В называется событие С, состоящее из всех элементарных событий, которые входят в А, но не входят в В. Обозначают: С = А – В или С = А\В. Замечание: событие А-В состоит в том, что событие А произошло, а событие В не произошло. Виды случайных событий Опр8: пространство элементарных событий называется достоверным, а пустое множество называется невозможным событием. Замечание!: достоверное событие в результате испытаний неизбежно происходит, а невозможное заведомо не может произойти. Опр9: события А и В называются несовместными, если их произведение есть невозможное событие, т. е. АВ = Ø, в противном случае события называются совместными. Замечание: несовместные события не могут наступить одновременно, а совместные могут. Опр10: событие Ā = Ω – А называется п ротивоположным событию А. Замечание: событие Ā (не А) означает, что событие А не произошло. Говорят, что соб А входит в соб В, или соб А влечет за собой соб В и пишут: А Св-ва операций над событиями: 1) А+ Классич. опред-е вер-ти Вер-ть Р(А) соб А равна отношению кол-ва эл-х событий m, входящих в состав события А к кол-ву всех возможных эл-х событий n: Р(А)=|A| / |Ω|=M/n З Символ |М| обозначает число эл-в любого конечного мн-ва М (мощность мн-ва) З! Классич. опред-е вер-ти примен-ся тогда, когда: 1) простр-во эл-х событий Ω конечно, т.е. |Ω|=n (конечное число) 2)все эл-ые события ωi- равновер-тны (равновозможны), т.е Р(ωi)=1/n для ¥ i=1,2…n Св-ва вер-ти: 1) Р(ω)=1 2) Р(Ø)=0 3) 0≤Р(А) ≤1, для ¥ А 4) Р( Лекция 4. Схема Бернулли Опр1. Испытание называется независимым если вер-ть какого либо исхода каждого из них не зависит от того какие исходы имели другие испытания. Опр2. Повторные независимые испытания называются испытаниям Бернулли или схемой Бернулли, если: 1) каждое испытание имеет только 2 возможных исхода; 2) вероятности этих исходов постоянны для всех испытаний, т.о. в схеме Бернулли для каждого испытания имеется только 2 исхода: событие А(успех) и событие не А (неудача) с постоянными вероятностями Р(А)=Р и Р(неА)=q при этом Р+q=1. Замечание. для n испытаний Бернулли элем. события удобно обозначать комбинациями в виде цепочек длиной n состоящих из букв У(успех) и Н (неудача), либо из букв А(успех) и неА(неудача), т.е. ω=УУН…ННУàn; =ААнеА…неАнеААàn Замечание. Испытания Бернулли возникают и при более сложных экспериментах, если мы не будем различать несколько возможных исходов, а опишем результат каждого испытания только в виде двух исходов А(успех), неА(неудача). Теорема (Формула Бернулли) Вероятность того что при n испытаний Бернулли успех наступит ровно m-раз равна Pn(m)=C n m *P^m*q^n-m, m-0,1,2,…,n, где Р -вероятность появления успеха в каждом испытании q=1-P-вероятность неудачи. Док-во. Обозначим интересующее событие Вn(m)={в n испытаниях Бернулли событие А(успех) наступит ровно m раз}. Представим событие Вn(m) через элементарные события например: при n=3 и m=2 будем иметь В3(2)= ААнеА+АнеАА+неААА. В общем виде событие Вn(m) представляет собой сумму элементарных событий в виде цепочек длиной n, каждая из которых состоит ровно из m событий А и (n-m) событий неА, т.е. Bn(m)=А,А,…,А* неА,неА,…,неА+АА…А*неААнеА…неА+…+неАнеА…неААА…А (*). В силу независимости испытаний вероятность каждой цепочки в формуле (*) равна Р(ААнеА….неАА)=Р(А)Р(А)Р(неА)…Р(неА)Р(А)=Р^m(A)*Р^n-m(неА)=Р^n*q^n-m А-m раз Р(А)- m раз неА(n-m)-раз Р(неА)-(n-m) раз Общее число цепочек в формуле(*)равно числу способов выбора из n испытаний m испытаний, в которых событие А произошло, т.е. равно числу сочетаний С n m. В связи с тем, что цепочки между собой несовместны получаем: Рn(m)=P(Bn(m))=P^m*q^n-m+P^m*q^n-m+…+P^m*q^n-m=С n m *P^m*q^n-m. Опр3. число m0 называется наивероятнейшим числом наступлений события А в n испытаниях Бернулли, если Рn(m0)>=Pn(m), m=0,1,2,….,n Замечание: наивероятнейшее число m0=целой части числа (n+1)*P и может быть определено из двойного неравенства: np-q<=m0<=np+q, если р≠0, р≠1. Если число (n+1)*p-целое, то наивероятнейшим так же будет являться и число m0-1, с той же вероятностью Pn(m0).
Свойства ФР. 1) 0<=F(x)<=1; 2)F(x)-неубывающая функция своего аргумента, т.е. если х1<x2, то F(x1)<F(x2); 3) F(-∞)=0; 4) F(+∞ =1; 5)P{a<=x<=b} =F(b)-F(a). Функция распределения ДСВ. Если Х –ДСВ, принимающая значение х1, х2, х3, и т. д. с вероятностями р1, р2, р3, и т. д., то её ФР задается равенством: F(x)=Σ(xi<x)pi, где суммируются вероятности тех значений xi, которые меньше х. Замечание: ФР любой ДСВ есть разрывная ступенчатая функция (непрерывная слева), скачки которой происходят в точках х1, х2, х3 и т.д. и равны вероятности р1, р2,р3 и т.д. Опр8: Плотность распределения или плотность вероятности НСВ Х в точке х называется производная её функции распределения в этой точке. Обозначают f(x): f(x)=F’(x) Замечание: плотность вероятности как закон распределения имеет смысл только для НСВ. Опр9: График плотности вероятности f(x) называется кривой распределения. Свойства плотности вероятности. 1)f(x)>=0; 2) -∞∫+∞f(x)dx=1;)P{a<=x<=b}= a∫bf(x)dx; 4)F(x)=-∞ ∫xf(t)dt(позволят находить функцию распределения по заданной плотности вероятности).
Св-ва Дисперсии D(x)=M(x)2 –M2 (x) D(c)=0 – где с- константа D(cx)=c2D(x), c-const D(x+-y)=D(x)+D(y) – если Х и У независимы. Опр-е: Ср. квадратичным отклонением (СКО) СВ наз-ся кв. корень от ее дисперсии σ(Х)= √D(x) Зам-е. размерность величин М(Х) и σ(Х) совпадает с размерностью самой СВ Х, а размерность D(X) равна квадрату размерности СВ Х. Опр. Модой ДСВ Х наз-ся ее наиболее вероятное значение, а модой НСВ Х наз-ся такое ее зн-е, при котором плотность вероятности достигает максимума, обозн. Мо(Х). Зам-ние. Если плотность вероятности достигает максимума не в одной, а в нескольких точках, то распределение называется полимодальным. Опр. Медианой Ме(Х) НСВ Х наз-ся такое ее зн-е, при к-м P{x>Me(X)}=P{x<Me(X)}=0.5. Зам. Геометричесик медиана НСВ Х - это такая точка Ме(Х) на оси Ох, для которой вертикальная прямая х=Ме(Х) делит площадь фигуры от кривой распр-я на 2 равные части Опр 8 Квантилем уровня р(или p- квантелем) СВ наз-ся такое значение хp, при котором вып-ся равенство F(xp)=p. Зам-ние. Медиана CD есть квантель уровня 0.5, т.е. Ме(Х)=х0.5. Опр. Начальным методом к-го порядка СВ наз-ся число nК=М(ХК). Центральным моментом к-го порядка СВ Х наз-ся число μК= М[x-M(x)]К.
Лекция 9 О пр1 Говорят, ДСВ Х имеет геометр распределение если она принимает значения 1,2.. (множество натуральных чисел) с вероятностями, где З! ДСВ х имеющая геометр распределение представляет собой число испытаний Бернулли которые нужно провести до 1 ого появления события А (успех). З! Ряд распределения ДСВ Ч имеющий геометр распределение имеет вид: При этом Вероятности pm= Т1. Мат ожидание и дисперсия СВХ имеющий геометрическое распределение соответственно равны: М(х)=1/р D(x)= Док: Поскольку множество возможных значений СВ Х бесконечно(счётно), то её мат ожидание есть сумма ряда M(x) т.к. члены ряда то Следовательно М(х)=р* Для вычисления дисперсии найдем сначала средний квадрат
= Следовательно: D(x)= M
Параграф 2 Гипергеометрическое распределение Говорят, что ДСВ Х имеет гипергеометрическое распределение если она принимает значения 0,1,2.., min(n,M) c вероятностями P{X=m}=
Теорема 2 математическое ожидание и дисперсия СВ Химеющей гипергеометрическое распределение соответственно равны M(x)= Зам. Гипергеометрическое распределение широко используется в практике статистического контроля качества промышленной продукции
Лекция 12 Опр 1. Плотностью вероятности 2мерной НСВ (X,Y) называется вторая смешанная частная производная её функции распределения:
Опр 2. График плотности вероятности 2 мерной НСВ называется поверхностью распределения. Свойства плотности вероятности двумерной НСВ f(x,y)больше или равно 0 Вероятность попадания случайной точки () в область D равна 2му интегралу от плотности вероятности по этой области т.е.
Функция распределения двумерной НСВ может быть выражена через её плотность вероятности по формуле:
Условия нормировки: 2ой несобственный интеграл в бесконечных пределах от плотности вероятности двумерной НСВ равен единице т.е.
Геометрически данное свойство означает, что объем тела, ограниченного сверху поверхностью распределения, а снизу плотностью x по y равна 1
Равномерное распределение 2мерной НСВ Опр3. Говорят, что двумерное НСВ (X,Y) имеет равномерное распределение в области D, если её плотность вероятности имеет вид: f(x,y)= где SD – площадь P замечание: Основные свойства равномерного распределения состоит в том,что для него применимо понятие “Изометрической вероятности” т.е. если область g содержится в области D, то нетрудно показать, что
Теорема (о независимости 2 СВ) СВ независимы
Доказательство: Необходимо: Пусть СВ x и y независимы, тогда
Достаточно: Пусть Тогда из определений функций распределения следует равенство: Следствие:Необходимым и достаточным условием независимости 2ух непрерывных СВ X и Y образующих систему (x,y) является равенство:
Лекция 13 Опр. 1. Условным законом распределения СВ Х входящей в систему (X,Y) называется её закон распределения вычисленный при условии, что другая СВ Y приняла определенное значение. Замечание. Аналогично определяется условный закон распределения СВ Y входящей в систему (X,Y). Обозначим через Замечание! Условные вероятности Опр. 2. Условным законом распределения составляющий x при Замечание. Аналогично находят условный закон распределения составляющий Y Замечание. Сумма вероятностей условного распределения равна 1. Док-во:
Аналогично доказывается, что при фиксированным Опр.3. Условной плотностью вероятности
Лекция 14 Опр. 1. МО двумерной ДСВ (X,Y) называется совокупность двух МО M(X) и M(Y) определяемых равенствами Опр. 2. МО двумерной НСВ с плотностью вероятности f(x,y) называется совокупность двух МО M(x) и M(y) определяемые равенствами Опр. 4. Дисперсией двумерной НСВ (X,Y) с плотностью вероятности f(x,y) называется совокупность двух дисперсий D(x) и D(y) определяемых равенствами Опр.5.Ковариацией СВ X и Y называется МО произведения отклонений этих величин. Обозначается cov (X,Y) или Замечание! Ковариацию часто удобно вычислять по формуле, которая получается из определения ковариации на основании свойств МО СВ X и Y называется выражение
Теория вероятности Лекция№1 Случайные события Опр1: опыт, эксперимент, наблюдение явления будем называть испытанием. Опр2: произвольное множества Ω (омега) называем пространством элементарных событий, а элементы ω (омега) этого множества будем называть элементарными событиями (элементарными исходами). Замечание: элементарным событием соответствует взаимоисключающие исходы опыта (испытания). Опр3: произвольное подмножество пространство элементарных событий называется случайным событием или просто событием. Обозначают: А, В, С… Опр4: говорят, что в результате испытания осуществилось (наступило) событие А, если произошло элементарное событие ω Є А. Операции над событиями Опр5: суммой событий А и В называется событие С, состоящее из всех элементарных событий, которые входят или в событие А или в событие В или в то и другое. Обозначают: С = А + В или С = A U В. Замечание: событие А + В состоит в том, что произошло по крайней мере одно из двух событий А или В. Опр6: произведением событий А и В называется событие С, состоящее из всех элементов, которые одновременно входят в обои события А и В. Обозначают: С = АВ или С = А ∩ В. Замечание: событие АВ происходит тогда и только тогда, когда происходят одновременно и событие А, и событие В. Опр7: разностью событий А и В называется событие С, состоящее из всех элементарных событий, которые входят в А, но не входят в В. Обозначают: С = А – В или С = А\В. Замечание: событие А-В состоит в том, что событие А произошло, а событие В не произошло. Виды случайных событий Опр8: пространство элементарных событий называется достоверным, а пустое множество называется невозможным событием. Замечание!: достоверное событие в результате испытаний неизбежно происходит, а невозможное заведомо не может произойти. Опр9: события А и В называются несовместными, если их произведение есть невозможное событие, т. е. АВ = Ø, в противном случае события называются совместными. Замечание: несовместные события не могут наступить одновременно, а совместные могут. Опр10: событие Ā = Ω – А называется п ротивоположным событию А. Замечание: событие Ā (не А) означает, что событие А не произошло. Говорят, что соб А входит в соб В, или соб А влечет за собой соб В и пишут: А Св-ва операций над событиями: 1) А+ Классич. опред-е вер-ти Вер-ть Р(А) соб А равна отношению кол-ва эл-х событий m, входящих в состав события А к кол-ву всех возможных эл-х событий n: Р(А)=|A| / |Ω|=M/n З Символ |М| обозначает число эл-в любого конечного мн-ва М (мощность мн-ва) З! Классич. опред-е вер-ти примен-ся тогда, когда: 1) простр-во эл-х событий Ω конечно, т.е. |Ω|=n (конечное число) 2)все эл-ые события ωi- равновер-тны (равновозможны), т.е Р(ωi)=1/n для ¥ i=1,2…n Св-ва вер-ти: 1) Р(ω)=1 2) Р(Ø)=0 3) 0≤Р(А) ≤1, для ¥ А 4) Р( Лекция №2 Вероятность событий 1. Элементы комбинаторики. Комбинаторика изучает количество различных комбинаций, которые можно составить из элементов произвольного конечного множ-ва. Перестановками -называются комбинации составленные из одних и тех же n различных элеметнов, которые отличаются между собой только порядком расположения элементов. Общее число перестановок равно Pn!=n!=1*2*3*4…n Пример: х={1,2,3} 123 132 213 231 312 321 Опр2. сочетанием -называется комбинации составленные из n различных элементов по m элементов которые отличаются между собой хотя бы 1 элементом. C n m = n!/m!(n-m)! Замечание: в сочетание порядок расположение элементов не важен. Опр3. размещениями наз-ся комбинации составленные из n различных элементов по m, которые отличаются составом элементов, либо их порядком. Общее число размещений A n m =n!/(n -m)!=n(n-1)…(n-m+1)- m сомножителей Опр4. (геометрическое определение вероятности) если g часть области G, то при бросании на удачу точки в область G вероятность ее попадания в часть g= P=mes g/mes G, где символ mes означает мера (в одномерном варианте длина, двумерном-площадь, в трехмерном - объем) Замечание. При геометрическом определении вероятности полагают: 1. пространство элементарных событий (Ω=G) 2. интересующее событие A=g опр.5 (условная вероятность) вероятность события А, найденное при условии, что событие B уже произошло, называется условной вероятностью события А, и обозначается символом P(A/B) опр6. (независимость событий) 2 события А и В называются независимыми если вероятности появления каждого из них не зависит от того произошло ли другое событие или нет, т.е. если: P(A/B)=P(A), P(B/A)=P(B). При этом вероятности P(A) и P(B) называют безусловными вероятностями в противном случае события называют независимыми. Замечание. зависимость и независимость событий всегда взаимно т.е. если А зависит от В то и В зависит от А, и наоборот. Кроме того, если события А и В независимы то независимы каждые 2 события А и В, А и В, А и В Замечание. На практике о независимости событий заключают по смыслу задачи. Теорема сложения вероятностей. Вероятность суммы двух событий А и В = сумме вероятностей этих событий минус вероятность их произведения. P(A+B)=P(A)+P(B)-P(AB). Следствие: если события А и В не совместны то P(A+B)=P(A)+P(B) Теорема умножения вероятностей. Вероятность произведения двух событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии что первое событие уже наступило P(AB)=P(A)*P(B/A)=P(B)*P(A/B) Следствие. Если события А и В независимы то Р(АВ)=Р(А)*Р(В)
Лекция 3Формула полной вероятности, формула Байеса. Опр1. (полная группа событий) говорят что совокупность событий А1, А2…Аn образуют полную группу событий, если эти события попарно несовместны и в результате испытания обязательно наступает хотя бы одно из них, т.е. если: 1. Ai*Aj=Ø(невозможные события), при I неравно j. 2. A1+A2+…+An=Ω Замечание!: для одного и того же испытания может быть несколько полных групп событий. Торема1. сумма вероятностей событий А1, А2 …Аn образующих полную группу,равна 1. P(A)+P(B)+…+P(An)=1 Док-во: поскольку события А1,А2,…,Аn образуют полную группу, то А1+А2+…+Аn= Ω. Отсюда Р(А1+А2+…+Аn)=Р(Ω)=1(*). Любые два события полной группы несовместны, поэтому Р(А1+А2+…+Аn)=Р(А1)+Р(А2)+…+Р(Аn)(**). Из формул (*) и (**) окончательно получаем P(A)+P(B)+…+P(An)=1 Теорема (формула полной вероятности) если событие А может наступить только при условии появления одного из событий В1, В2…Вn, которое образуют полную группу событий, то вероятность события А равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: P(A)=Σ P(Bi)*P(A/Bi) Док-во. Поскольку события В1, В2…Вn образуют полную группу, то В1+ В2+…+Вn=Ω поэтому А=А*Ω=А(В1+ В2+…Вn)=АВ1 +АВ2 + +..АВn=Σ ABi. Т.к. события В1, В2… Вn попарно несовместны то и события АВ1, АВ2…АВn так же попарно несовместны Р(А)=Р(Σ АВi)=Σ P(ABi)=Σ P(Bi)*P(A/Bi) Замечание. ФПВ применяется во всех случаях когда испытание со случайным исходом распадается на 2 этапа, на первом этапе как бы «разыгрывается» условие испытание, а на втором этапе его результат, событие В1, В2… Вn при этом обычно называются гипотезами, поскольку за ранее неизвестно какое из этих событий наступит. Формула Байеса. P(Bi/A)=P(Bi)P(A/Bi))/(Σ P(Bi)P(A/Bi)) Доказательство. По теореме умножения вероятностей имеем P(A/Bi)=P(A)* P(Bi/A)=P(Bi)* P(A/Bi) отсюда P(Bi/A)=(P(Bi)*P(A/Bi))/P(A)(*). С другой стороны по формуле полной вероятности P(A)=Σ P(Bi)*P(A/Bi)(**). Из формулы (*)и(**) получаем формулу Байеса Замечание. Формула Байеса позволяет пересчитывать вероятности гипотез в свете новой инфо-ии, состоящей в том, что в результате опыта произошло событие А. Аксиомотическое построение теории вероятности (проеодолевает недостатки, присущие известным опред вероятности.-автор Толмогоров) 1.Каждому событию А соотв неотриц числоP(А), назыв его вероятностью. 2.Вероятность достоверного соб-ия =1P(гамма)=1 3. Если А1,А2,А3,Аn попарно несовм, то P(A1+A2+A3+An)=P(A1)+P(PA2)+P(An) Лекция 4. Схема Бернулли Опр1. Испытание называется независимым если вер-ть какого либо исхода каждого из них не зависит от того какие исходы имели другие испытания. Опр2. Повторные независимые испытания называются испытаниям Бернулли или схемой Бернулли, если: 1) каждое испытание имеет только 2 возможных исхода; 2) вероятности этих исходов постоянны для всех испытаний, т.о. в схеме Бернулли для каждого испытания имеется только 2 исхода: событие А(успех) и событие не А (неудача) с постоянными вероятностями Р(А)=Р и Р(неА)=q при этом Р+q=1. Замечание. для n испытаний Бернулли элем. события удобно обозначать комбинациями в виде цепочек длиной n состоящих из букв У(успех) и Н (неудача), либо из букв А(успех) и неА(неудача), т.е. ω=УУН…ННУàn; =ААнеА…неАнеААàn Замечание. Испытания Бернулли возникают и при более сложных экспериментах, если мы не будем различать несколько возможных исходов, а опишем результат каждого испытания только в виде двух исходов А(успех), неА(неудача). Теорема (Формула Бернулли) Вероятность того что при n испытаний Бернулли успех наступит ровно m-раз равна Pn(m)=C n m *P^m*q^n-m, m-0,1,2,…,n, где Р -вероятность появления успеха в каждом испытании q=1-P-вероятность неудачи. Док-во. Обозначим интересующее событие Вn(m)={в n испытаниях Бернулли событие А(успех) наступит ровно m раз}. Представим событие Вn(m) через элементарные события например: при n=3 и m=2 будем иметь В3(2)= ААнеА+АнеАА+неААА. В общем виде событие Вn(m) представляет собой сумму элементарных событий в виде цепочек длиной n, каждая из которых состоит ровно из m событий А и (n-m) событий неА, т.е. Bn(m)=А,А,…,А* неА,неА,…,неА+АА…А*неААнеА…неА+…+неАнеА…неААА…А (*). В силу независимости испытаний вероятность каждой цепочки в формуле (*) равна Р(ААнеА….неАА)=Р(А)Р(А)Р(неА)…Р(неА)Р(А)=Р^m(A)*Р^n-m(неА)=Р^n*q^n-m А-m раз Р(А)- m раз неА(n-m)-раз Р(неА)-(n-m) раз Общее число цепочек в формуле(*)равно числу способов выбора из n испытаний m испытаний, в которых событие А произошло, т.е. равно числу сочетаний С n m. В связи с тем, что цепочки между собой несовместны получаем: Рn(m)=P(Bn(m))=P^m*q^n-m+P^m*q^n-m+…+P^m*q^n-m=С n m *P^m*q^n-m. Опр3. число m0 называется наивероятнейшим числом наступлений события А в n испытаниях Бернулли, если Рn(m0)>=Pn(m), m=0,1,2,….,n Замечание: наивероятнейшее число m0=целой части числа (n+1)*P и может быть определено из двойного неравенства: np-q<=m0<=np+q, если р≠0, р≠1. Если число (n+1)*p-целое, то наивероятнейшим так же будет являться и число m0-1, с той же вероятностью Pn(m0).
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.156.58 (0.009 с.) |

 , если все эл-ые события мн-ва А входят в В
, если все эл-ые события мн-ва А входят в В =Ω 2) А
=Ω 2) А  =Ø 3) (А+В)С=АС+ВС 4)
=Ø 3) (А+В)С=АС+ВС 4)  =
=  *
*  5)
5)  =
= 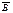 6) А*Ω=А
6) А*Ω=А , q=1-p m=1,2, …
, q=1-p m=1,2, …
 образуют геометрическую прогрессию с первым членом р и q. Отсюда и вытекает название Геометрическое распределение.
образуют геометрическую прогрессию с первым членом р и q. Отсюда и вытекает название Геометрическое распределение.
 =
= 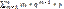 =
=  =
= 
 являются производными по переменной q соответствующих членов ряда
являются производными по переменной q соответствующих членов ряда  и при этом:
и при этом: 
 =
= 
 =
= 
 =
=  =
=  =
=  =
=  =
= p*(q(-
p*(q(- 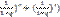 = p*(q(-
= p*(q(- 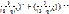 p*(q(-
p*(q(-  p*(q(-
p*(q(-  p*(-
p*(-  p*(-
p*(- 
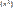 - M2(x)
- M2(x)  =
=  ч.т.д.
ч.т.д. , где m=0,1,…min(n,M)
, где m=0,1,…min(n,M) , где n,M,N натуральные числа
, где n,M,N натуральные числа

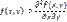


 =1
=1 )=
)=  )=
)= 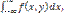 где
где  и
и  ) плотность вероятности СВ(X,Y) соответственно.
) плотность вероятности СВ(X,Y) соответственно.
 где
где  площадь g
площадь g функция распределения двумерной СВ (X,Y) равна произведению функций распределения составляющих т.е.
функция распределения двумерной СВ (X,Y) равна произведению функций распределения составляющих т.е.
 )= F(x,y),
)= F(x,y), 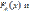
 ) функции распределения СВ x и y соответственно.
) функции распределения СВ x и y соответственно.
 )
)
 )
) , которое и означает, что СВ X и Y независимы ч.т.д.
, которое и означает, что СВ X и Y независимы ч.т.д.
 )= F(x,y)
)= F(x,y) условную вероятность, того что СВ Х примет значение
условную вероятность, того что СВ Х примет значение  при условии, что СВ Y приняла значение
при условии, что СВ Y приняла значение 
 определяются равенством:
определяются равенством: 
 называют совокупность условных вероятностей
называют совокупность условных вероятностей 
 Вычисленных предположений, что событие уже наступило.
Вычисленных предположений, что событие уже наступило.





 . Это свойство распределений используют для контроля вычислений.
. Это свойство распределений используют для контроля вычислений. составляющей X при заданном значении Y=y называется отношение плотности вероятности двумерной непрерывной СВ (X,Y) к плотности вероятности составляющей Y т.е.
составляющей X при заданном значении Y=y называется отношение плотности вероятности двумерной непрерывной СВ (X,Y) к плотности вероятности составляющей Y т.е.  Аналогично определяется условная плотность вероятности составляющей Y при заданном значении X=x
Аналогично определяется условная плотность вероятности составляющей Y при заданном значении X=x  Формулы для вычисления условных плотностей вероятностей. Если известна плотность вероятности f(x,y) двумерной непрерывной СВ (X,Y), то условные плотности вероятности составляющих X и Y могут быть найдены по формулам
Формулы для вычисления условных плотностей вероятностей. Если известна плотность вероятности f(x,y) двумерной непрерывной СВ (X,Y), то условные плотности вероятности составляющих X и Y могут быть найдены по формулам 
 Замечание! Условные плотности вероятности обладают всеми свойствами безусловной плотности вероятности.
Замечание! Условные плотности вероятности обладают всеми свойствами безусловной плотности вероятности.
 , где
, где 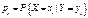 .
.
 . Опр. 3. Дисперсией двумерной ДСВ (x,y) называется совокупность двух дисперсий D(x) и D(y) определяемых равенствами
. Опр. 3. Дисперсией двумерной ДСВ (x,y) называется совокупность двух дисперсий D(x) и D(y) определяемых равенствами 
 .
.
 З! МО M(x),M(y) и дисперсии D(x),D(y) СВ X и Y входящих в систему (X,Y) могут быть найдены по обычным формулам используемых для одномерных СВ. Для этого необходимо предварительно перейти от закона распределения двумерной СВ (X,Y) соответственно к одномерным законам распределения СВ X и Y
З! МО M(x),M(y) и дисперсии D(x),D(y) СВ X и Y входящих в систему (X,Y) могут быть найдены по обычным формулам используемых для одномерных СВ. Для этого необходимо предварительно перейти от закона распределения двумерной СВ (X,Y) соответственно к одномерным законам распределения СВ X и Y
 . Замечание. Ковариация характеризует взаимную зависимость СВ X и Y
. Замечание. Ковариация характеризует взаимную зависимость СВ X и Y  - Для ДСВ
- Для ДСВ  -НСВ
-НСВ . Если СВ независимы то k=0. Опр.6. Коэф. корреляции
. Если СВ независимы то k=0. Опр.6. Коэф. корреляции . Замечание! Для любых СВ X и Y выполняется соотношение
. Замечание! Для любых СВ X и Y выполняется соотношение 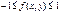 , при этом если r=0, то СВ X и Y называются некореллированы, в противном случае – кореллированы.
, при этом если r=0, то СВ X и Y называются некореллированы, в противном случае – кореллированы.


