Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула полной вероятности. Формула Байеса.Содержание книги
Поиск на нашем сайте
Пусть дана группа несовместных событий В1,В2…Вn и некоторое событие А, подразделяющееся на частные случаи АВ1, АВ2… АВn. И пусть даны вероятности P(В1), P(В2),…,P(Вn) и условные вероятности P(A|В1), P(A|В2),…,P(A|Bn). Требуется определить вероятность P(A). Так как A = АВ1 +АВ2 +…+ АВn, то P(A)= P(АВ1 + АВ2 +… +АВn). События В1, В2,…,Вn несовместные, следовательно, события АВ1,АВ2,…,АВn тоже несовместные. Воспользуемся теоремой сложения для несовместных событий. P(A) = P(АВ1 + АВ2 +… +АВn) = P(АВ1)+ P(АВ2)+… +P(АВn) По теореме умножения для каждого слагаемого имеем P(ABi)=P(Bi)P(A|Bi). Следовательно P(A) = P(B1)P(A|B1) +P(B2)P(A|B2)+…+P(Bn)P(A|Bn). Или
Пусть дана группа несовместных событий В1, В2,…Вn и некоторое событие А, подразделяющееся на частные случаи АВ1, АВ2,… АВn. И пусть даны вероятности P(В1), P(В2),…,P(Вn) и условные вероятности P(A|B1), P(A|В2),…,P(A|Вn). Требуется определить условные вероятности P(В1|A), P(В2|A),…,P(Вn|A). По теореме умножения P(AB) = P(B)P(A|B) или P(AB) = P(A)P(B|A). Следовательно, P(B)P(A|B)=P(A)P(B|A). Воспользуемся последним равенством и выразим P(B|A) в общем случае
P(A) находим по формуле полной вероятности
Итак, Вер-ть Р(Вi) осуществления соб. Вi (i = 1,…,n), вычисл. безотносительно к соб. А, нзв априорной вер-тью (a priori). Усл. вер-ть Р(Вi|А) выполнения соб. Вi (i = 1,…,n), вычисл. в предположении, что соб. А осуществилось, нзв апостериорной вер-тью (a posteriori). События Вi называют гипотезами, а теорему Байеса теоремой гипотез.
Формулы полной вероятности и Байеса связаны между собой и дают прямое и обратное решения одной и той же проблемы. Первая прогнозирует возможность появления события А по известным до опыта вероятностям осуществления гипотез. Последняя оценивает вероятность осуществления каждой гипотезы, если событие А произошло. 7.Случайные величины. Основные свойства функции распределения. Дискретные непрерывные случайные величины. Случайной нзв величину, к-рая в рез-те испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случ.причин, к-рые заранее не могут быть учтены. Опр: Случайной величиной ξ(w) нзв. ф-ция элементарных событий от w с обл. определений Ω и обл. значений действ. чисел R1 и означает, что событие {w: ξ(w)£ x }Î σ-алгебре F при х Î R1. Значение х нзв реализацией случ-ой вел-ны ξ(w). Сов-ть всех реализаций сл. вел-ны, т.е. обл. значений ξ(w), нзв. спектром знач. сл. величины. Ф-ция распределения случ-ой величины. σ-алгебра мн-ва F предст.соб. класс событий, для к-рых определена вер-ть
Опр: Пусть у нас есть ξ – случ.вел-на и х – произвольное действительное число. Вер-ть того, что ξ меньше, чем х, нзв ф-цией распред. вер-тей сл. вел-ны ξ.
Для описания случайной величины ξ необходимо указать множество её возможных значений х и задать распределение вер-тей этих значений. Опр: Пусть ξ(w) сл. вел-на и х произвольное действительное число вер-ти. Тогда вер-ть того, что ξ(w) примет значение, меньшее, чем х, нзв ф-цией распред. вер-тей сл. вел-ны ξ(w).
Замечание: ф-ция распределения явл. разновидностью закона распределения для сл. величин всех типов и однозначно опред. случ. величину. Св-ва ф-ции распред. 1) Ф-ция распред. Fξ(x) опред. для всех х на действ. прямой.
2) Ф-ция распред. неотриц. и не больше 1.
Ф-ция
3) Док-во: ξ<+∞ достоверно, отсюда Р(ξ<+∞)=1. Ak – событие, состоящее в том, что k-1£ξ<k. Bn={ξ£ –n} n=1, 2,… Bn+1={x£ – (n+1)} Í Bn(ξ£ –n) "n³1.
Аналогично док-ся для х→-∞. 4) Ф-ция распределения не убывает. Если x1<x2, то F(x1)-F(x2)=P{x1£x<x2}, при этом F(x1)£F(x2). Д-во: " x1<x2, {ξ<x2}={ξ£x1}+{x1<ξ£x2}. {ξ£x1}×{x1<ξ£x2}=Æ. По А3: F(x2)=P{ξ<x2}=F(x1)+P{x1<ξ£x2} => F(x2)-F(x1)= P{x1<ξ£x2} > 0. 5) ф-ция распред.непрерывна слева
Док-во: По А4: Дискретные и непрерывные случайные величины. Опр: числовая ф-ция ξ= ξ(w) опред на пространстве Ω и принимающая конечное или счетное множество значений х1, х2, …, хn, нзв дискретной случайной величиной, если для любого xi мн-ва w, для к-рых ξ(w)=xi, принадлежит σ-алгебре мн-ва F, т.е.
Ф-ция распред. любой дискретной сл.вел-ны разрывна, возрастает скачками при тех значениях х, к-рые явл.возмож.значениями. Распределение дискрет.сл.вел-ны есть ступенчатая ф-ция. Единичной ступенчатой ф-цией (ф-цией Хевисайда) нзв ф-ция вида Опр: числовая ф-ция ξ=ξ(w), опред. на пространстве Ω и прин-щая несчетное кол-во значений (-∞; +∞), нзв непрерывной сл. вел-ной, если любое xi мн-ва w, при к-рых ξ(w)<x, принадлежит σ-алгебре мн-ва F, т.е.
Если сл.вел-на ξ имеет абсолютно непрерыв.ф-цию распред. Fξ(x), для к-рой существ.неотриц.ф-ция f(x), удовл. при любых х рав-во
то в этом случае сл.вел-на нзв непрерывной, а ф-ция f(x) нзв плотностью распред.ее вер-тей. Ф-ция распр.непрерыв.сл.вел-ны сама явл.непрерыв.
Математическое ожидание случайной величины и его свойства. Начальные и центральные моменты случайной величины. Условное математическое ожидание. Дисперсия случайной величины и её свойства. Связь различных случайных величин. Коэффициент корреляции и его свойства Матожидание: Опр: мат.ожиданием (или средним значением случайной величины ξ) нзв величина M[ξ], к-рая опред след образом:
Пример дискретной величины:
Кубик: N=6 {1,2,3,4,5,6} M[ξ]=1/6(1+3+3+4+5+6)=3,5 => Вероятнее всего, выпадет 3 или 4. Пример непрерывной величины: ξ - точка координат, брошенная на удачу на отрезок [a;b]
Св-ва мат.ожидания: 1) мат. ожид. постоянной равно ей самой M[c]=c, c=const. M[1]=1 2) постоянную величину можно вынести за знак мат. ожидания M[c+ξ]=M[ξ]+c M[c*ξ]=cM[ξ] 3) мат.ожидание суммы любых случ-ых величин равно сумме их математических ожиданий, если эти мат.ожидания существуют. "ξ, η M[ξ+η]=M[ξ]+M[η] 4) мат. ожидание произведения независимых случайных величин равно произведению их мат.ожиданий ξ, η – независ. M[ξ×η]=M[ξ]×M[η] 5) если ξ£η при всех элемент.исходах, то их мат.ожидания сохраняют соотношение: M[ξ]£M[η]. Начальные и центральные моменты случайной величины: Опр: начальным моментом k-ого порядка случайной величины ξ нзв. мат.ожидание k-ой степени этой случайной величины
Опр: центральным моментом k-ого порядка случайной величины ξ нзв мат.ожидание k-ой степени центрированной случайной величины
Центрированной сл.вел-ной нзв разность м/у сл.вел-ной ξ и ее мат. ожиданием.
Условное математическое ожидание:
где Ai – полная группа несовмест.событий, Дисперсия случайной величины: Опр: дисперсией случ.величины ξ нзв. мат.ожидание квадрата отклонения случ.величины ξ от её мат.ожидания.
Дисперсия характеризует степень рассеивания реализации случайной величины около её мат.ожидания. Св-ва дисперсии 1) дисперсия постоянной величины равно нулю D[c]=0, с=const 2) 3) Дисперсия суммы любых случайных величин равна сумме дисперсий этих величин (если эти дисперсии существуют)
4) если дисперсия случ. величны ξ равна нулю, то ξ равна постоянной с вероятностью, равной единице: если D[ξ]=0, то ξ = Const с вероятностью р =1 5) дисперсию можно посчитать по формуле:
Две сл. вел-ны могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми. Строгая функ-ная зав-ть реализуется редко, т.к. обе величины или одна из них подвержены еще действию случ.факторов, причем среди них могут быть и общие для обеих величин. В этом случае возникает статистическая зависимость. Стат-кой нзв зав-ть, при к-рой изменение одной из величин влечет изменение распределения другой. В частности, стат.зав-ть проявл.в том, что при изменении одной из величин изменяется среднее значение другой. В этом случае стат.зав-ть нзв корреляционной. Коэффициент корреляции r Коэффициентом корреляции rξη сл.вел-н ξ и η нзв отношение корреляционного момента к произведению сред.квадр.отклонений этих вел-н:
или
Свойства коэффициента корреляции: 1) для независимых случайных величины ξ и η коэ-нт корреляции равен нулю. Сл.вел-ны ξ и η нзв некоррелированными, если их коэф-т кор-ции равен 0. 2) коэ-нт корреляции лежит в пределе от -1 до 1 3) если r=1 или r=-1, то величины ξ и η линейно зависимы (прямая или обратная зав-ть соответственно)
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 172; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.92.50 (0.008 с.) |

 Формула полной вероятности
Формула полной вероятности - формула полной вероятности
- формула полной вероятности Формула Байеса
Формула Байеса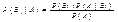

 - формула Байеса
- формула Байеса ,
, 


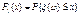



 определенная на всей числовой прямой R нзв ф-цией распределения случ-ой величины.
определенная на всей числовой прямой R нзв ф-цией распределения случ-ой величины. Например: х принимает значение -1 с вер-тью ½ и значение 1 с вер-тью ½. Тогда
Например: х принимает значение -1 с вер-тью ½ и значение 1 с вер-тью ½. Тогда


 для любого элементарного исхода знач. ξ вещественно и не может быть меньше всех веществ.чисел, т.е. пересечение Bn не содерж. элем.исходов.
для любого элементарного исхода знач. ξ вещественно и не может быть меньше всех веществ.чисел, т.е. пересечение Bn не содерж. элем.исходов.
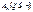







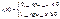



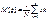





 Если условная ф-ция распределения случ. величины ξ: Fξ(x|A), то в этом случае можно рассчитать усл.мат. ожид. по формуле:
Если условная ф-ция распределения случ. величины ξ: Fξ(x|A), то в этом случае можно рассчитать усл.мат. ожид. по формуле: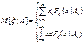
 - ф-ции распред. ξ. M[ξ|A] нзв услов.мат.ожид.сл.вел-ны относительно события А.
- ф-ции распред. ξ. M[ξ|A] нзв услов.мат.ожид.сл.вел-ны относительно события А.


 Связь различных сл.вел-н.
Связь различных сл.вел-н.
 где
где