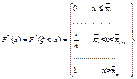Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные непрерывные распределения. Равномерное распределение. Экспоненциальное распределение. Нормальное распределение. Логарифмически нормальное распределение.Содержание книги
Поиск на нашем сайте
Основные непрерывные распределения Случайная величина ξ имеет абсолютно непрерывное распределение, если существует неотрицательная функция fξ(x) такая, что для любого xÎR функция распределения Fξ(x) представима в виде
При этом функция fξ(x) называется плотностью распределения случайной величины ξ. Виды непрерывных распред.: равномерное, нормальное (гауссовское), показательное (экспоненциальное), логарифмически нормальное.
Равномерное распр.
Равномер распр явл непрерывным аналогом дискр распр-я вер-ей для опытов с равновероятностными исходами.
Экспоненциальное распределение.
Нормальное распределение. Опред: Случ вел-на ξ имеет нормальное (Гауссовское) распр-е с параметрами a и σ (σ >0), если имеет место след плотность распр-ия:
Свойства: 1. Fa,σ 2(x)=F0,1((x-a)/σ) xÎR 2. ξ (x1, x2) P(x1≤ξ≤ x2)=Ф((x2-a)/σ) – Ф((x1-a)/σ) 3. Ф-ция распр сл вел-ны ξ, распред-ой по норм закону, выражается через ф-цию Лапласа по формуле: Fξ(x)=½+Ф((x-a)/σ)
Логарифмически нормальное распределение. Опред: Лог-ски норм распр-ем наз-ся распр-ие вер-ти неотриц случайной вел-ны ξ, логарифм кот-ой распределен по норм-му закону с параметрами a и σ, σ>0. a=M[ln ξ] σ2=D[ln ξ]
Числовые характеристики:
13. Закон больших чисел. Неравенство Чебышёва. Правило 3σ. Теорема Чебышёва. Теорема Бернулли. Центральная предельная теорема. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа. Закон больших чисел Свойства статистической устойчивости средних заключается в том, что индивидуальные особенности, присущие каждому конкретному случайному явлению, почти не сказываются на усредненном результате таких явлений. Закон больших чисел – это несколько теорем, определяющих общие условия, при которых среднее значение случайных величин стремится к некоторой const при проведении большого числа опытов (теоремы Чебышева и Бернулли).
Если существует последовательность таких, что для любых ε>0, выполняется условие:
Последовательность
Если в выражении (*) В данных терминах Неравенство Чебышева Для любой случайной величины ξ(кси), имеющей M[ξ] и D[ξ] при каждом ε>0 имеет место неравенство(неравенство Чебышева):
Док-во: ξ£η, M[ξ]£M[η] Рассмотр. некотор.сл.вел-ну η
Пример: пусть ε=3σ Случайная величина окажется за пределами 3σ:
Верно для любого распределения. Это – верхняя граница распределения вер-ти. Противоположное событие – в пределах 3σ:
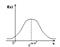
Правило 3σ
99,73% 0,27% - неудача (практически невозможное событие) Правило 3σ: Если случайная величина имеет нормальное распределение, то отклонение этой величины от мат ожидания по абсолютной величине не превосходит утроенного среднеквадратического отклонения. Теорема Чебышева Если
Док-во:
следовательно, при n→∞
Теорема Бернулли Пусть m – число наступлений события А в n независимых испытаний и Р – вероятность наступления события А в каждом из испытаний при любом ε>0.
С ростом числа испытаний относительная частота успехов (m/n) будет приближаться к единичной вероятности. Вводим случайную величину
Центральная предельная теорема Если то при неограниченном возрастании n (n→∞) закон распределения суммы случайных величин
Пусть
Локальная предельная теорема Муавра-Лапласа Если вероятность наступления некоторого события в n независимых испытаниях постоянна и равна Р (0<Р<1), то вероятность для х>0 φ(-х)=φ(х) Интегральная теорема Муавра-Лапласа Если k – число наступления события в n независимых испытаниях, в каждом из которых вероятность этого события = Р, то равномерно относительно а и b, связанных так: – ∞ ≤ а ≤ b ≤ + ∞, имеет место соотношение при n→∞:
Функция Лапласа:
Ф(– х)= – Ф(х)
при n→∞. Если n конечно
Векторные случайные величины. (2.)Свойства двумерной случайной величины. (3.)Двумерная дискретная случайная величина, её геометрическая интерпретация. (4.)Функция распределения и её свойства. (5.)Матрица распределения. (6.)Двумерная непрерывная случайная величина, её геометрическая интерпретация. (7.)Плотность распределения двумерной случайной величины и её свойства. (8.)Понятие независимости для двумерных случайных величин. (9.)Критерии независимости. (1.) Кроме одномерных, случайных величин можно рассматривать многомерные, случайные векторы, координаты которых являются одномерными, случайными величинами. Пример: 1) Успеваемость ученика 2)Погода в данное время в данном месте. Случайная векторная величина принимает каждый раз значения, зависящие от элементарного события. Таким образом, многомерная, случайная величина есть вектор-функция, заданная на пространстве элементарных событий, и каждое ее возможное значение есть вектор. Будем обозначать через (X, Y) двумерную сл.вел-ну. Каждую из вел-н Х и Y нзв составляющей (компонентой); обе вел-ны Х и Y, рассматриваемые одновременно, образуют систему двух сл.вел-н. Аналогично n-мерную вел-ну можно рассматривать как систему n сл.вел-н. Например, трехмерная вел-на (X, Y, Z) определяет систему трех сл.вел-н X, Y и Z. Целесообразно различать дискретные (составляющие этих вел-н дискретны) и непрерывные (составляющие этих вел-н непрерывны) многомерные сл.вел-ны. В теоретеко-множественной трактовке любая случайная величина Xi(i=1,2,…n) есть функция элементарных событий ω, входящих в пространство элементарных событий Ω (ωÎΩ). Поэтому и многомерная случайная величина есть функция элементарных событий ω, т.е. каждому элементарному событию ставится в соответствие несколько действительных чисел х1,х2,…xn, которые приняли случайные величины Х1,Х2, …Хn в результате испытания. В этом случае вектор х=(х1,х2,…хn) называется реализацией случайного вектора Х= (Х1,Х2, …Хn). На вероятностном пространстве {Ω,F,P} определены n-мерные сл.вел-ны ξ1=f1(w), ξ2=f2(w), …, ξn=fn(w) (fi(w) измеримы). Вектор (ξ1, ξ2,…, ξn) нзв случ.вектором или n-мерной сл.вел-ной. Обозначим мн-во элемент.событий w {ξ1<x1, ξ2<x2, …, ξn<xn}, для к-рых одноврем.выполняется неравенство f1(w)<x1, f2(w)<x2, …, fn(w)<xn, при этом {ξ1<x1, ξ2<x2, …, ξn<xn}ÎF. Тогда при любом наборе х1, х2,…,xn выполняется равенство F(х1, х2,…,xn)=P{ξ1<x1, ξ2<x2,…, ξn<xn}. Эта ф-ция n-аргументов нзв n-мерной ф-цией распределения сл.вектора (ξ1, ξ2,…, ξn). Многомерная случайная величина полностью определяется ее функцией распределения вероятностей, удовл. след.условиям: 1. 0£ F(х1, х2,…,xn)£1 2. F(х1, х2,…,xn) не убывает по каждому аргументу 3. 4. (2.) Двумерная сл.вел-на (ξ, h) – это совокупность 2-х одномерных сл.вел-н, к-рые принимают значения в рез-те проведения одного и того же опыта. Двумерные сл.вел-ны характеризуются мн-вами значений Ωξ и Ωh своих компонент и совместными (двумерными) законами распределения. В зав-ти от типа компонент ξ и h, различают дискретные, непрерывные и смешанные сл.вел-ны. (3.) Двумерная случайная величина называется дискретной, если составляющие ее случайные величины являются дискретными. Двумерную сл.вел-ну (ξ, η) геометрически можно изобразить либо как случайную точку М(ξ, h) на плоскости (т.е. как точку со случ.координатами), либо как случ.вектор ОМ.
(4.) Ф-цией распред. Fξη(x, y) двумерной сл.вел-ны (ξ, η) нзв вер-ть совместного выполнения события (ξ<x, η<y), т.е. такая ф-ция F(x, y), к-рая определяет для каждой пары чисел х, у вер-ть того, что ξ примет значение, меньшее х, и при этом η примет значение, меньшее у: Fξη(x, y)=Р(ξ<x, η<y).
Св-ва ф-ции распределения двумерной сл.вел-ны: 1. 0£ Fξη(x, y)£1 Вытекает из опред-я ф-ции рапред.как вер-ти: вер-ть – всегда неотриц.число, не превышающее 1. 2. Fξη(x, +∞)= Fξ(x), т.к. Fξη(x, +∞)=Р(ξ<x, η<+∞)=Р(ξ<x)= Fξ(x) Fξη(+∞, y)= Fη(y) аналогично 3. Fξη(x, -∞)= Fξη(-∞, у)= Fξη(-∞, -∞)=0. Вытекает из невозможности событий. Fξη(+∞, +∞)=1. Вытекает из достоверности событий. 4. Fξη(x, y) есть монотонно неубывающая ф-ция по каждому аргументу. Д-во: Событие, состоящее в том, что составляющая ξ примет значение, меньшее х2, и при этом составляющая η<y, можно подразделить на два несовмест.события: 1) ξ примет значение, меньшее х1, и при этом η<y с вер-тью Р(ξ<x1, η<у); 2) ξ примет значение, удовлетворяющее нер-ву х1£ξ<х2, и при этом η<y с вер-тью Р(х1£ξ<х2, η<y). По теореме сложения, Р(ξ<x2, η<у)= Р(ξ<x1, η<у)+ Р(х1£ξ<х2, η<y). Отсюда Р(ξ<x2, η<у) – Р(ξ<x1, η<у) = Р(х1£ξ<х2, η<y) или Fξη(x2, y) - Fξη(x1, y)= Р(х1£ξ<х2, η<y). Любая вер-ть есть число неотриц., поэтому Fξη(x2, y) - Fξη(x1, y)³0, или Fξη(x2, y)³Fξη(x1, y) ч.т.д. Аналогично доказывается, что Fξη(x, y) неубывающая по аргументу у.
(5.) Законом распред.дискретной двумерной сл.вел-ны нзв перечень возможных значений этой вел-ны, т.е пар чисел (xi, yj) и их вероятностей р(xi, yj) (i=1, 2,…,n; j=1, 2,…, m). Обычно закон распределения задают в виде матрицы. Матрица распред.предст.соб.таблицу, к-рая содержит значения {x1, x2,…, xn}, {y1, y2,…, yn} и вероятности возможных пар значений Pij=P(ξ=xi; η=yj) (i=1, 2,…,n; j=1, 2,…, m).
Св-ва: 1) 2) 3) (6.) Двумер.сл.вел-на (ξ, η) является непрерывной, если ее ф-ция распред.предст.соб. непрерывную дифференцированную ф-цию по каждому из аргументов и существует 2-ая смешанная производная. Пространством ее элементарных событий является плоскость, либо область плоскости, либо область конечной ненулевой плоскости.
(7.) Двумерной плотностью ф-ции распред. fξη(x, y) случ.вел-ны (ξ, η) нзв предел отношения вер-ти попадания случ.точки в элементарный участок плотности, примыкающий к точке (х, у), к площади этого участка, когда его размер стремится к 0.
Свойства двумерной плотности распределения: 1) 2) Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен 1.
3) 4) (8.) Величина ξ независима от величины η,если её закон распределения не зависит от того, какое значение принимает величина η. Теорема. Для того, чтобы случ.вел-ны ξ и h были независимыми, необходимо и достаточно, чтобы ф-ция распред.системы (ξ, η) была равна произведению ф-ций распределения составляющих
Следствие. Для того, чтобы непрерывные случайные величины ξ и h были независимыми, необходимо и достаточно, чтобы плотность совмест.распред.системы (ξ, η) была равна произведению плотностей распред.составляющих:
(9.) Критерии независимости: 1) 2) Непрерывность
3) Дискретность
Если хотя бы один из критериев не выполняется в любой одной точке, то величины ξ и η зависимы.
Условные распределения двумерной случайной величины. Функция распределения и её свойства. Условная плотность распределения и её свойства. Условные числовые характеристики. Корреляционные зависимости. Нормальный закон распределения двумерной случайной величины. Случайные величины: ξ xi i=1÷n; η yj j=1÷m. Условной функцией распределения случайной величины ξ, при условии, что случайная величина η приняла значение yi называется условная вероятность.
Свойства условной ф-ции распределения: 1) Fξ(x|y) – определена для всех х 2) Fξ(x|y) Î [0,1] для всех х Î R 3) Fξ(-∞|y)=0 4) Fξ(+∞|y)=1 5) Сумма вероятностей распределения равна 1. Имеем yi: Имеем xi: Используют для контрольного вычисления. Условная плотность распределения и её свойства Условной плотностью распределения fξ(x/y) непрерывной случайной величины ξ при фиксированном значении η=у называется отношение плтности совместного распределения fξη(x/y) случайной величины (ξ,η) к плотности распределения случайной величины ξ.
Свойства: 1) fξ(x/y)≥0 2) fξ(x/y) – непрерывная функция 3) 4) ξ и η – независимы
5) Условные числовые характеристики Условным мат ожиданием случайной величины ξ называют её мат ожидание, вычисленное при условии, что случайная величина η приняла значение у.
Условное мат ожидание M[ξ|y] случайной величины ξ как функция параметра у называется регрессией ξ на у
Смешанный начальный момента порядка K+S равен мат ожиданию
Смешанные центральный момент K+S равен мат ожиданию произведения центрированных величин
Следствия:
Корреляционные зависимости Корреляционным моментом (kξη) случайных величин ξ и η называют мат ожидание произведения отклонения этих величин от их мат ожидания: Характеризует степень тесноты линейных величин ξ и η и их рассеивание их значений относительно точки Свойства: 1) kξη = kηξ 2) Корреляционный момент двух независимых случайных величин ξ и η равен 0. 3)Абсолютная величина корреляционного момента двух случайных величин ξ и η не превышает среднего геометрического их дисперсий:
Если kξη<0, то между ξ и η существует отрицательная корреляционная зависимость(если одно значение растет, то другое значение уменьшается). Если kξη >0, то между ξ и η существует положительная корреляционная зависимость(если одно значение растет, то и другое значение растет).
Коэффициент корреляции (rξη) случайных величин ξ и η называется отношение корреляционного момента к произведению среднего квадратических отклонений этих величин: -1≤ rξη ≤1 Две случайные величины ξ и η называются коррелированными, если их корреляционный момент отличен от нуля. Соответственно, ξ и η называются некоррелированными, если их корреляционный момент равен нулю.
rξη=1; ξ и η; η=аξ+b
Нормальный закон распределения двумерной случайной величины Непрерывная двумерная случайная величина (ξ,η) имеет нормальное распределение, если её плотность вероятности равна:
Параметрами нормального закона распределения являются:
Если случайные величины распределены нормально, но они некоррелированны, то rξη=0, и получим:
Таким образом, если составляющие нормального распределенной случайной величины некоррелированны, то плотность совместного распределения системы равна произведению плотностей распределения составляющих.
16. Многомерные случайные величины.Основные характеристики (Ф-я распределения, плотность распр-я, понятие независимости). Основные числовые характеристики (мат.ожидание, дисперсия, корреляционная матрица, коэф-т корреляции, нормированная корреляционная матрица). Опр. Совокупность произвольного числа n одномерных случ. вел-н Опр. Ф-я распределения n-мерной случ. величины
Опр. Плотность распред-я n-мерной случ. величины наз. смешанная частная производная функции распределения F(х1,х2,…,хn), взятая один раз по каждому аргументу. Св-ва плотности рапр-я: 1. f(x1,x2,…,xn)³ 0 2. 3. Плотности распределения меньшего порядка могут быть получены путем интегрирования n-мерной плотности распр-я по ненужным переменным. 4. Вер-ть попадания многомер.случ.величины
Опр. Случайные величины f(x1,x2,…,xn)=f1(x1)f2(x2)…fn(xn)
Основные числовые характеристики. 1. Вектор мат. ожидания. M=(m1,m2,…,mn)
2. Вектор дисперсии. D=(D1,D2,…,Dn)
3. Корреляционная матрица.
где kij=kji - т.е. матрица симметрична.
Замечание: случ. величины 4. Коэф-т корреляции.
5. Корреляционная нормированная матрица
Случ. величины ! Если случ. величины независимы, то они некоррелируемы, НО обратное утверждение НЕВЕРНО!
Коэффициентом корреляции (rξη) случ вел ξ и η наз.отношение корреляц.момента к произведению среднеквадратич.отклонений этих величин
-1≤ rξη ≤1
Основные задачи математической статистики. Генеральная и выборочная совокупность. Повторная и бесповторная выборка. Репрезентативность выборки. Теоретическая ФР. Статистическое распределение выборки. Эмпирическая функция распределения. Гистограмма, полигон относительных частот. Статистические оценки параметров распределения (выборочная, средняя, групповая и общая средняя, выборочная дисперсия). Формула для вычисления дисперсии. Статистика разрабатывает методы сбора данных и группировки по умолчанию. Задачи мат стат.: 1) указать способы сбора и группировки стат. сведений, полученных в рез-те наблюдения за случ. процессами; 2) разработка методов анализа стат. данных в зависимости от цели исследования. Генеральная и выборочная совокупность: Генеральной совокупностью опыта наз. множ-во объектов, из к-ых производится выборка. Выборочной совокупностью или просто выборкой наз. совокупность случайно отобранных объектов. {х1, х2, …, хn} n-объём выборки Объёмом совокупности (выборочной или генеральной) наз. число объектов этой совокупности. Повторная и бесповторная выборка. Репрезентативность выборки. Теоретическая ФР. Повторной наз.выборку, при к-ой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной наз.выборку, при к-ой отобранный объект в генеральную совокупность не возвращается. Выборка будет репрезентативной, если её осуществлять случайно, то есть каждый из объектов генеральной совокупности имеет одинаковую вероятность попасть в выборку. k-кол-во выборок, которые можно сделать n-объём выборки x:
…………………
Пусть x®Fξ(x) – функция распределения, тогда каждую из следующих выборок:
можно рассмотреть как реализацию n-мерной случайной величины (ξ1, ξ2,…, ξn) Для всех ξi закон распределения единственный. Все компоненты (ξi) – независимы. Тогда F(х1,х2,…,хn)=F(x1)F(x2)…F(xn) Вариационным рядом наз.выборка
В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности наз. теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том,что теоретическая функция F(x) определяет вер-сть события X<x, а эмпирическая функция F*(x)=nx/n определяет относительную частоту этого же события. Статистическое распределение выборки: x1 – наблюдается n1 раз x2 – n2 xk – nk
ni - частота
Замечание: В теории вероятности под распределениями понимают соответствие между возможными значениями случ.величины и их вер-тями. А в мат.статистике – соответствие между наблюдаемыми вариантами и их частотами. Эмпирическая функция распределения: nx-число наблюдений, при которых наблюдалось значение признака варианты меньше, чем х n-общее число наблюдений (объём выборки) x<x
Эмперической функцией распределения случ.величины x наз.функцию F*ξ(x), определяющую для каждого значения x относительную частоту событий:
Недостатки: Невысокая наглядность (визуально сложно определить закон распределения сл.величины x) Гистограмма и полигон относит.частот: Полигоном частот наз.ломаную, отрезки к-ой соединяют xi и ni.
Площадь гистограммы частот =сумме всех частот, то есть объёму выборки.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.46.24 (0.011 с.) |

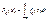
 Сл вел-на ξ имеет равномер распред на отрезке [a;b] с несчет мн-вом возм значений, если плотность распр ξ постоянна на отрезке [a;b] и = 0 вне его.
Сл вел-на ξ имеет равномер распред на отрезке [a;b] с несчет мн-вом возм значений, если плотность распр ξ постоянна на отрезке [a;b] и = 0 вне его.



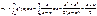
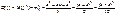

 Случ вел-на ξ имеет экспоненц-ое (показательное) распр с параметром α>0, если имеет место след посл-ть распределения:
Случ вел-на ξ имеет экспоненц-ое (показательное) распр с параметром α>0, если имеет место след посл-ть распределения: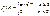

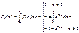




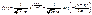



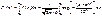

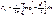
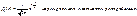


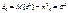


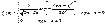




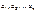
 (*)
(*) подчиняется закону больших чисел с заданными функциями
подчиняется закону больших чисел с заданными функциями  :
:
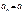 , то говорят, что случайная величина
, то говорят, что случайная величина  сходится по вероятности к а.
сходится по вероятности к а. означает, что вел-на ηn-an сходится по вероятности к нулю.
означает, что вел-на ηn-an сходится по вероятности к нулю.






 последовательность попарнонезависмых случайных величин, имеющих конечное мат ожидание
последовательность попарнонезависмых случайных величин, имеющих конечное мат ожидание  и дисперсия, ограниченная одной и той же постоянной
и дисперсия, ограниченная одной и той же постоянной  то при любом ε>0, предел вероятности события стремится к 1 при n→∞:
то при любом ε>0, предел вероятности события стремится к 1 при n→∞:
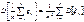

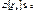
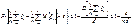


 - число наступлений события А в k-ом испытании.
- число наступлений события А в k-ом испытании.

 и третий центральный абсолютный момент:
и третий центральный абсолютный момент: 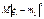 и если выполняется условие Ляпунова:
и если выполняется условие Ляпунова: 
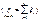 неограниченно приближается к нормальному закону с параметрами:
неограниченно приближается к нормальному закону с параметрами: 
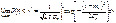

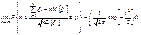
 того, что в этих испытаниях событие А наступит ровно k раз при n→∞ удовлетворяет соотношению:
того, что в этих испытаниях событие А наступит ровно k раз при n→∞ удовлетворяет соотношению: 






 где F(xi) – ф-ция распред.одномерной сл.вел-ны ξi.
где F(xi) – ф-ция распред.одномерной сл.вел-ны ξi.
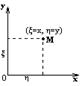
 Геометрически это можно истолковать так: Fξη(x, y) есть вер-ть того, что случ.точка (ξ, η) попадет в бесконечный квадрант с вершиной (х, у), расположенные левее и ниже этой вершины.
Геометрически это можно истолковать так: Fξη(x, y) есть вер-ть того, что случ.точка (ξ, η) попадет в бесконечный квадрант с вершиной (х, у), расположенные левее и ниже этой вершины. 5. Если двумерн.ф-ция распред. Fξη(x, y) непрерывна по х и по у, то вер-ть попадания случ.вел-ны (ξ, η) в прямоугольную область D={х1 £ x £ х2, y1 £ y £y2} равна Р(х1£ξ£х2, у1£ η £у2) = F(x1, y1)+F(x2, y2) – F(x1, y2) – F(x2, y1).
5. Если двумерн.ф-ция распред. Fξη(x, y) непрерывна по х и по у, то вер-ть попадания случ.вел-ны (ξ, η) в прямоугольную область D={х1 £ x £ х2, y1 £ y £y2} равна Р(х1£ξ£х2, у1£ η £у2) = F(x1, y1)+F(x2, y2) – F(x1, y2) – F(x2, y1).
 ,
, 
 ,
, 


 Т.о. плотностью совместного распределения вер-тей двумерной непрерывной сл.вел-ны нзв вторую смешанную частную производную от ф-ции распред. Геометрически эту ф-цию можно истолковать как поверхность, к-рую нзв поверхностью распределения.
Т.о. плотностью совместного распределения вер-тей двумерной непрерывной сл.вел-ны нзв вторую смешанную частную производную от ф-ции распред. Геометрически эту ф-цию можно истолковать как поверхность, к-рую нзв поверхностью распределения. D={х1£ ξ £х2, у1£ η £у2}
D={х1£ ξ £х2, у1£ η £у2}


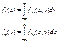


 для всех х, у
для всех х, у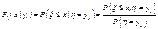


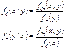












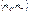




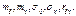

 , кот. принимают значения одного и того же опыта наз. n-мерной случ. величиной:
, кот. принимают значения одного и того же опыта наз. n-мерной случ. величиной: 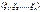 .
. наз. вероятность выполнения n-неравенств вида:
наз. вероятность выполнения n-неравенств вида:
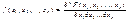 .
.

 в n-мерную область D=n-кратному интегралу по этой области.
в n-мерную область D=n-кратному интегралу по этой области.
 наз. независимыми, если закон распред. каждой частной системы, выделенной из системы
наз. независимыми, если закон распред. каждой частной системы, выделенной из системы 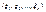 не зависит от того, какие значения приняли остальные величины.
не зависит от того, какие значения приняли остальные величины.




 – будут некоррелированные,если их недиагональные элементы корреляц-ой матрицы=0.
– будут некоррелированные,если их недиагональные элементы корреляц-ой матрицы=0.
 Rij=Rji
Rij=Rji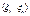 - независимы, если
- независимы, если 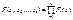 , где F – ф-ция распред.случ величины.
, где F – ф-ция распред.случ величины.


 ,
,  …..
….. 
 полученная в рез-те расположения значений исходной выборки в порядке возрастания.
полученная в рез-те расположения значений исходной выборки в порядке возрастания.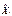 наз. вариантами.
наз. вариантами.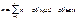
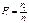 -относительная частота
-относительная частота
 -частота события, когда x<x
-частота события, когда x<x