
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические оценки. Точечные оценки. Метод максимального правдоподобия. Метод наименьших квадратов. Интервальные оценки.Содержание книги
Поиск на нашем сайте
Стат.оценкой неизвестного параметра теоретического распределения нзв ф-цию от наблюдаемых случайных величин. Несмещенной нзв стат.оценку, мат.ожид.к-рой равно оцениваемому параметру Q при любом объеме выборки, т.е. M[Q*]=Q. Смещенной нзв оценку, мат.ожид.к-рой не равно оцениваемому параметру. Эффективной нзв оценку, к-рая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.
Точечные оценки Точечной нзв оценку, к-рая опред-ся одним числом, например: генеральная средняя, выборочная средняя, групповая и общая средние, генеральная дисперсия, выборочная дисперсия и др.
xi – значения выборки При выборке малого объема точечная оценка может знач.отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Несмещенной оценкой генеральной средней (мат ожидания) служит выборочная средняя
варианты xi, Замечание1.Если первоначальные варианты xi-большие числа,то для упрощения расчета из каждой варианты одно и то же число С,т.е. перейти к условным вариантам ui=xi-C, тогда Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
Замечание2.Если первоначальные варианты xi-большие числа, то целесообразно вычесть из всех вариант одно и то же число C,равное выборочной средней или близкое к ней,т.е. перейти к условным вариантам ui=xi-C (дисперсия при этом не изменится). Тогда
Замечание 3. Если первоначальные варианты являются десятичными дробями с k десятичными знаками после запятой, то, чтобы избежать действий с дробями,умножают первоначальные варианты на постоянное число C=10k,т.е. переходят к условным вариантам ui=Cxi. При этом дисперсия увеличится в C2 раз. Поэтому, найдя дисперсию условных вариант, надо разделить ее на C2:
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия
В условных вариантах она имеет вид
Причем если ui=xi-C,то s2x= Примечание 4. При большом числе данных используют метод произведений или метод сумм.
Метод максимального правдоподобия. Метод м.п. точечной оценки неизвестных параметров заданного распределения сводится к отысканию максимума ф-ции одного или нескольких оцениваемых параметров. А) Дискретные случ величины. Пусть Х-дискретная случ величина,кот в результате n опытов приняла возможные значения х1,х2..хn.Допустим,что вид закона распределения случ велич Х задан,но неизвестен параметр Q,которым определяется этот закон;требуется найти его точечную оценку Q*=Q*(х1,х2..хn). Обозначим вероятность того,что в результате испытания величина Х примет значение хi через p(xn; Q). Функцией правдоподобия дискретной случайной величины Х назыв ф-цию аргумента Q: L(х1,х2..хn; Q)=p(x1; Q)* p(x2; Q)… p(xn; Q). Оценкой наибольшего правдоподобия параметра Q назыв такое его значение Q*,при кот ф-ция правдоподобия достигает максимума.Функции L и lnL достигают максимума при одном и том же значении Q,поэтому вместо отыскания максимума ф-ции L ищут,что удобнее,максимум ф-ции lnL. Логарифмической ф-цией правдоподобия назыв ф-цию lnL.Точку максимума ф-ции lnL аргумента Q можно искать,например,так: 1.найти производную 2.приравнять производную 0 и найти критич точку Q*-корень получ ур-ия (ур-ия правдоподобия) 3.найти вторую производную Б) Непрерывные случайные величины. Пусть Х-непрерывн случ велич,которая в результате n испытаний приняла значения х1,х2..хn. Допустим,что вид плотности распределения-ф-ции f(x) – задан,но неизвестен параметр θ,которым определяется эта ф-ция. Ф-ией правдоподобия непрерывной случ величины Х назыв ф-цию аргумента Q: L(х1,х2..хn; Q)=f(x1; Q)* f(x2; Q)… f(xn; Q). Оценку наибольшего правдоподобия неизвестного параметра распределения непрерывной случ величины ищут также,как в случае дискретной случ величины. Если плотность распределения f(x) непрерывной случ величины определяется двумя неизвестными параметрами Q1и Q2,то ф-ция правдоподобия есть ф-ция двух независ аргументов Q1и Q2: L= f(x1; Q1, Q2)* f(x2; Q1, Q2)… f(xn; Q1, Q2). Далее находят логарифмическую ф-цию правдоподобия и для отыскания ее максимума составл и решают систему
Метод наименьших квадратов а0, а1,…,an
(m+1) уравнений y=ax+b (x1, y1), (x2, y2)…
Интервальные оценки Интервальной нзв оценку, к-рая определяется двумя числами – концами интервала. Инт.оценки позволяют установить точность и надежность оценок. Надежностью (доверительной вероятностью) оценки Q по Q* нзв вер-ть γ, с к-рой осуществл.нерав-во |Q - Q*|<δ. Заменив нерав-во |Q - Q*|<δ равносильным ему двойным нерав-вом -δ<Q - Q*<δ или Q*-δ<Q<δ+Q* имеем
Доверительным нзв интервал (Q*-δ, Q*+δ), к-рый покрывает неизвестный параметр с заданной надежностью γ. 1.Интервальной оценкой (с надежностью γ) математического ожидания а нормально распределенного количественного признака X по выборочной средней
Где
2. Интервальной оценкой (с надежностью γ) среднего квадратического отклонения σ нормально распределенного количественного признака X по «исправленному» выборочному среднему квадратическому отклонению s служит довер. инт-л
Где q находят по таблице по заданным n и γ 3. Интервальной оценкой (с надежностью γ) неизвестной вер-ти p биноминального распред-я по относ. частоте ω служит довер.инт-л (с приближ. концами p1 и p2)
где
Где n-общее число испытаний; m-число появлений событий; ω-относ.частота, равная отношению m/n;t-значение аргумента ф-ции Лапласа, при к-ром Ф(t)=γ/2(γ-заданная надежность). Замечание. При больших значениях n (порядка сотен) можно принять в кач-ве приближ.границ довер.инт-ла
Статистическая проверка гипотез. Основные понятия. Статистический критерий, ошибки 1-го и 2-го родов, уровень значимости и мощность критерия. Критерий согласия Пирсона. Проверка гипотезы о значении параметров нормального распределения. Проверка гипотезы о законе распределения случайной величины. Статистическая проверка гипотез. Основные понятия. Уровень значимости и мощности критерия Статистической гипотезой наз всякое непротиворечивое множество утверждений
α =P{ZÎG|H0} где вероятность P соответствует условной плотности распределения f (z | H 0). Мощностью γ критерия согласия называется вероятность события, состоящего в том, что гипотеза H 0 отвергается, когда она неверна, т.е. γ=P{ZÎG|H1} где вероятность P соответствует условной плотности f (z | H 1). Критической точкой zβ называется точка на оси Oz, являющаяся квантилем уровня β=1 – α распределения F (z | H 0), соответствующего плотности распределения f (z | H 0). На рис. показана графическая интерпретация введенных понятий, где β + α = 1, δ + γ = 1.
Статистический критерий, ошибки 1-го и 2-го родов Ошибка 1-го рода состоит в отклонении гипотезы, если она верна (пропуск цели). Вероятность совершения ошибки 1-го рода обозначается α и наз. Уровнем значимости. Ошибка 2-го рода – гипотеза принимается, если она неверна – β (ложное срабатывание). Вероятность не совершить ошибку 2-го рода (1-β) наз. ложностью критерия. Критерием (статистическим критерием) наз. случайная величина
Проверка гипотез о законе распределения случайной величины. Критерий согласия Пирсона. Пусть имеется апостериорная выборка zn и требуется проверить гипотезу H 0, состоящую в том, что непрерывная СВ X имеет определенный закон распределения f (x) (например, нормальный, равномерный и т.д.). Истинный закон распределения f (x) неизвестен. Для проверки такой гипотезы обычно используют критерий согласия хи-квадрат χ² (критерий Пирсона).
Критерием согласия называется критерий, использованный для проверки гипотез о предполагаемом законе распределения. Проверка состоит в следующем: 1)Строится интервал - статистический ряд и гистограмма 2) По виду гистограммы
3) На основе выборки
4) Интервал возможных значений разбиваем на m непересекаемых интервалов. В каждом из них фиксируем число показаний 5) Вычисляем вероятность показаний ξ в каждом интервале 6) Строим критерий χ²
Аналитическое выражение плотности c²- сложное, поэтому задаем уровень значимости α; k; находим
Проверка гипотезы о значении параметров нормального распределения. Пусть известно, что СВ X имеет нормальное распределение. Требуется проверить гипотезу H 0, состоящую в том, что mX = m (m - некоторое фиксированное число), используя апостериорную выборку zn. Возможны два случая: дисперсия (σX)2 известна или неизвестна.
1) Дисперсия известна
2) Дисперсия неизвестна В качестве оценки вводим выборочную дисперсию В качестве статистики:
Гипотезы о значении дисперсии
|
||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.254.112 (0.007 с.) |

 Состоятельной нзв оценку, к-рая при n®∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n®∞ стремится к 0, то такая оценка оказывается и состоятельной.
Состоятельной нзв оценку, к-рая при n®∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n®∞ стремится к 0, то такая оценка оказывается и состоятельной.
 ,где xi –варианта выборки, ni-частота
,где xi –варианта выборки, ni-частота -объем выборки.
-объем выборки. .
. ,эта оценка является смещенной, т к
,эта оценка является смещенной, т к 




 ; если ui=Cxi, то s2x=
; если ui=Cxi, то s2x=  ,то s2x=
,то s2x= 
 ,если вторая производная при Q=Q* отрицательна,то Q*-точка максимума. Найденную точку максимума Q* принимают в качестве оценки наибольшего правдоподобия параметра Q.
,если вторая производная при Q=Q* отрицательна,то Q*-точка максимума. Найденную точку максимума Q* принимают в качестве оценки наибольшего правдоподобия параметра Q.
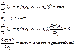


 при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал
при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал
 - точность оценки, n-объем выборки, t-значение аргумента ф-ции Лапласа Ф(t),при котором Ф(t)=γ/2; при неизвестном σ (и объеме выборки n<30)
- точность оценки, n-объем выборки, t-значение аргумента ф-ции Лапласа Ф(t),при котором Ф(t)=γ/2; при неизвестном σ (и объеме выборки n<30)
 (при q<1)
(при q<1) (при q>1)
(при q>1)



 относительно закона распределения случайной величины.
относительно закона распределения случайной величины.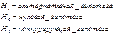
 Статистикой нзв произвольная функция Z = φ (Zn) выборки Zn, для значений к-рой известны условные плотности распределения f (z | H 0) и f (z | H 1) относительно проверяемой гипотезы H 0 и конкурирующей с ней альтернативной гипотезы H 1. Из опред следует, что Z есть СВ. Практическое применение мат. статистики состоит в проверке соответствия результатов экспериментов предполагаемой гипотезе. С этой целью строится процедура (правило) проверки гипотезы. Критерием согласия называется правило, в соответствии с которым по реализации статистики Z, вычисленной на основании апостериорной выборки zn, гипотеза H 0 принимается или отвергается. Критической областью G называется область реализаций z статистики Z, при которых гипотеза H 0 отвергается. Доверительной областью G называется область значений z статистики Z, при которых гипотеза H 0 принимается. Уровнем значимости α критерия согласия называется вероятность события, стоящего в том, что гипотеза H 0 отвергается, когда она верна, т.е.
Статистикой нзв произвольная функция Z = φ (Zn) выборки Zn, для значений к-рой известны условные плотности распределения f (z | H 0) и f (z | H 1) относительно проверяемой гипотезы H 0 и конкурирующей с ней альтернативной гипотезы H 1. Из опред следует, что Z есть СВ. Практическое применение мат. статистики состоит в проверке соответствия результатов экспериментов предполагаемой гипотезе. С этой целью строится процедура (правило) проверки гипотезы. Критерием согласия называется правило, в соответствии с которым по реализации статистики Z, вычисленной на основании апостериорной выборки zn, гипотеза H 0 принимается или отвергается. Критической областью G называется область реализаций z статистики Z, при которых гипотеза H 0 отвергается. Доверительной областью G называется область значений z статистики Z, при которых гипотеза H 0 принимается. Уровнем значимости α критерия согласия называется вероятность события, стоящего в том, что гипотеза H 0 отвергается, когда она верна, т.е.
 , которая позволяет принять или отклонить нулевую гипотезу.
, которая позволяет принять или отклонить нулевую гипотезу.














