
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность, случайное событие, случайная величинаСодержание книги
Поиск на нашем сайте
Теория вероятностей - это математическая наука, изучающая закономерности случайных событий. Вероятностным экспериментом (испытанием, наблюдением) называется эксперимент, результат которого нельзя предсказать заранее. В данном эксперименте любой его результат (исход) является событием. Событие может быть достоверным (всегда происходит в результате испытания); невозможным (заведомо не происходит при испытании); случайным (может произойти или не произойти в условиях данного эксперимента). Событие, которое нельзя разбить на более простые события, называется элементарным. Событие, представленное в виде совокупности нескольких элементарных событий, называется сложным (фирма не понесла убытки – прибыль может быть положительной либо равной нулю). Два события, которые не могут происходить одновременно (увеличение налогов – рост располагаемого дохода; увеличение объема инвестиций – снижение уровня риска), называются несовместными. Иными словами, два события несовместны, если появление одного из них исключает появление другого. В противном случае они являются совместными (увеличение объема продаж – увеличение прибыли). События называются противоположными, если одно из них происходит тогда и только тогда, когда не происходит другое (товар реализован – товар не реализован). Вероятность события – это численная мера, которая вводится для сравнения событий по степени возможности их появления. Классическое определение вероятности. Вероятностью Р (А) события А называется отношение числа m равновозможных элементарных событий (исходов), благоприятствующих появлению события А, к общему числу n всех возможных элементарных исходов данного эксперимента:
Из вышеизложенного вытекают следующие основные свойства вероятности: 1. 0 £ Р (А) £ 1. 2. Вероятность достоверного события А равна 1: Р (А) = 1. 3. Вероятность невозможного события А равна 0: Р (А) = 0. 4. Если события А и В несовместны, то Р (А + В) = Р (А) + Р (В); если же события А и В совместны, то Р (А + В) = Р (А) + Р (В) - Р (А . B). (Р (А . B) – вероятность совместного появления этих событий). 5. Если А и Если вероятность осуществления одного события не изменяет вероятности появления другого, то такие события называются независимыми. При непосредственном вычислении вероятностей событий, характеризующихся большим числом исходов, следует пользоваться формулами комбинаторики [12,13]. Для исследования группы событий (гипотез) применяются формулы полной вероятности, Бейеса и Бернулли (n независимых испытаний – повторение опытов) [12,16]. При статистическом определении вероятности события А под n понимается полное число фактически проведенных испытаний, в которых событие А встретилось ровно m раз. В этом случае отношение m / n называется относительной частотой (частостью) Wn (A) появления события А в n произведенных испытаниях. При определении вероятности по методу экспертных оценок под n понимается количество экспертов (специалистов в данной области), опрашиваемых на предмет возможности осуществления события А. При этом m из них утверждают, что событие А произойдет. Понятия случайного события недостаточно для описания результатов наблюдений величин, имеющих числовое выражение. Например, при анализе финансового результата предприятия в первую очередь интересуются его размерами. Поэтому понятие случайного события дополняется понятием случайной величины. Под случайной величиной (СВ) понимается величина, которая в результате наблюдения (испытания) принимает одно из возможного множества своих значений, заранее неизвестное и зависящее от случайных обстоятельств. Для каждого элементарного события СВ имеет единственное значение. Различают дискретные и непрерывные СВ. Для дискретной СВ множество ее возможных значений конечно или счетно, т. е. СВ принимает отдельные изолированные значения, которые могут быть заранее перечислены, с определенными вероятностями. Для непрерывной СВ множество ее возможных значений бесконечно и несчетно, например, все числа данного интервала, т.е. возможные значения СВ не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток. Примеры случайных величин: Х - ежедневное число покупателей в супермаркете (дискретная СВ); Y - число детей, родившихся в течение суток в определенном административном центре (дискретная СВ); Z - координата точки попадания артиллерийского снаряда (непрерывная СВ). Многие СВ, рассматриваемые в экономике, имеют настолько большое число возможных значений, что их удобнее представлять в виде непрерывных СВ. Например, курсы валют, доход населения и т. п. Для описания СВ необходимо установить соотношение между всеми возможными значениями СВ и их вероятностями. Такое соотношение будет называться законом распределения СВ. Для дискретной СВ его можно задать таблично, аналитически (в виде формулы) либо графически. Например, таблично для СВ Х
Обычно x 1 < x2 < … < xn. Обязательно Пример 1.1. Группа, состоящая из 20 студентов, сдаёт экзамен по теории вероятностей. Из группы 10 студентов получают оценку 3; 6 - оценку 4; 4 – оценку 5. Построить закон распределения дискретной СВ - бальной оценки, полученной случайно выбранным студентом. Решение данной задачи можно представить в виде таблицы:
Если по оси абсцисс откладывать значения случайной величины, а по оси ординат - соответствующие вероятности, то получаемая соединением точек ломанная линия является графическим изображением закона распределения и называется полигоном распределения вероятностей (многоугольником распределения). Аналитически СВ задается либо функцией распределения, либо плотностью вероятностей. Функцией распределения СВ Х называют функцию F (x), определяющую для каждого х вероятность того, что СВ Х примет значение, меньшее х: F (x) = P (X < x). (1.2) Из определения вытекают следующие свойства функции распределения: 1. 0 £ F (х) £ 1 – неотрицательная функция. 2. F (x) – неубывающая функция, т. е. при х 2 > x 1 F (x2) ³ F (x 1). 3. 4. Вероятность попадания СВ Х в интервал [ а, b) (включая а) равна приращению F (x) на этом интервале, т. е. Р (а £ х £ b) = F (x) - F (b). 5. P (X ³ x) = 1 – F (x). График функции распределения дает наглядное представление о вероятности изменения значений СВ. Для примера 1.1 функция распределения F (x) и ее график имеют вид:
Рис. 1.1. По мере увеличения числа возможных значений дискретной СВ и уменьшения интервалов между ними, число скачков (разрывов функции распределения) будет становиться все больше, а сами скачки – меньше; ступенчатая кривая становится все более плавной; т.е. дискретная СВ постепенно приближается к непрерывной величине, а ее функция распределения – к непрерывной функции. Для непрерывной СВ нельзя определить вероятность того, что она примет некоторое конкретное значение (точечную вероятность). Так как в любом интервале содержится бесконечное число значений, то вероятность выпадения одного из них асимптотически равна нулю. В результате непрерывную СВ нельзя задать таблично. Однако для описания непрерывной СВ может быть использована функция распределения и плотность вероятности (плотность распределения вероятностей). Плотностью вероятности непрерывной СВ Х называют функцию f (x), являющуюся производной ее функции распределения f(x) = F ’(x). (1.3) Плотность вероятности f (x) определяет закон распределения для непрерывной СВ. Свойства плотности вероятности: 1. f (x) ³ 0. 2. Вероятность попадания непрерывной СВ в интервал [ a, b ] равна определенному интегралу – 3. Функция распределения (рис. 1.2) может быть выражена через плотность вероятности по формуле:
4.
Рис. 1.2. Рис. 1.3.
Из определения плотности вероятности следует: tg α= f(m), где α- угол наклона касательной к кривой функции распределения F(x) в точке x= m (геометрический смысл производной функции).
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

 . (1.1)
. (1.1) противоположные события, то Р (
противоположные события, то Р ( (полная система несовместных событий).
(полная система несовместных событий). ,
,  , если значения случайной величины, расположены на всей оси х.
, если значения случайной величины, расположены на всей оси х.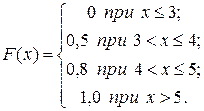

 т. е. площади заштрихованной фигуры (см. рис. 1.2). Вероятность попадания значений СВ в «хвосты» распределения, т. е. в интервалы (-¥, а) и (b; +¥), равна 1 – Р(а £ х £ b).
т. е. площади заштрихованной фигуры (см. рис. 1.2). Вероятность попадания значений СВ в «хвосты» распределения, т. е. в интервалы (-¥, а) и (b; +¥), равна 1 – Р(а £ х £ b).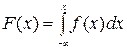 .
. – условие нормировки. Площадь под графиком кривой плотности вероятности f (x) равна единице (рис. 1.3).
– условие нормировки. Площадь под графиком кривой плотности вероятности f (x) равна единице (рис. 1.3).





