
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П.Б. Болдыревский, Зимина С.В.Содержание книги Поиск на нашем сайте
П.Б. Болдыревский, Зимина С.В.
ЭКОНОМЕТРИКА
Учебное пособие
Нижний Новгород Аннотация Материал учебного пособия разработан на основе лекций, читаемых авторами в течение ряда лет в Нижегородском государственном университете им. Н.И. Лобачевского студентам экономических специальностей. В учебном пособии в концентрированном виде представлена современная методология эконометрического моделирования. Рассмотрены основные элементы эконометрики. Изложены понятия парной, множественной регрессионных моделей, моделей временных рядов и их анализа. Обсуждаются такие вопросы практического многомерного моделирования как гетероскедастичность, мультиколлинеарность, фиктивные переменные, особенности спецификации модели. Учебный материал сопровождается определенным числом вопросов и задач для самопроверки. Для студентов (бакалавриат) экономических специальностей вузов, а также для магистрантов, аспирантов и специалистов, интересующихся методами обработки статистических данных и экономического анализа. ПРЕДИСЛОВИЕ
«Эконометрика» как учебная дисциплина, на современном этапе, благодаря своей универсальности и возможности практического использования для анализа реальных экономических объектов, является одним из базовых курсов в системе высшего экономического образования. В последние годы появились интересные учебники и учебные пособия по эконометрике. Однако, как показывают контакты авторов со студентами, аспирантами, преподавателями и специалистами, занимающимися экономическим анализом, ощущается нехватка доступных учебных пособий по данной дисциплине. В представленном учебном пособии авторами лаконично и на доступном уровне изложены основные вопросы эконометрического анализа, достаточно глубоко и полно рассмотрены базовые понятия эконометрики и регрессионного анализа. Учебное пособие ориентировано на начальный курс эконометрики, и, в первую очередь, предназначено для студентов (бакалавриат) экономических специальностей вузов. Представленный учебный материал направлен на формирование соответствующих профессиональных и общекультурных компетенций. Книга также может быть полезна магистрантам, аспирантам, специалистам и руководителям, изучающим статистические методы анализа экономических процессов и интересующимися прикладными исследованиями в области экономики. Изложение учебного материала предполагает, что читатель владеет основами теории вероятностей, математической статистики и линейной алгебры в объеме курса математики экономического или технического вуза.
Пособие состоит из введения, основного учебного материала (главы 1–7) и приложения, содержащего математико-статистические таблицы и методические указания по реализации типовых эконометрических задач на компьютере. В конце книги приведен развернутый предметный указатель основных понятий курса. Во введении рассмотрены основные цели и задачи эконометрики как науки, а также сформулированы основные понятия и этапы эконометрического моделирования. Поскольку основой методов и математического инструментария эконометрики являются теория вероятностей и математическая статистика, в первой главе приведены основные положения этих дисциплин, без которых невозможно понимание материала последующих глав. При этом особое внимание уделяется экономическим приложениям теории вероятностей и математической статистики. В главах 2–7 рассматриваются линейные и сводящиеся к линейным эконометрические модели, как наиболее применимые на практике для анализа и прогнозирования экономических процессов. Для большей наглядности при изложении материала приводятся примеры с решениями. Применение компьютерных пакетов для оценивания эконометрических моделей рассмотрено авторами учебников [25,28, 31]. Многие задачи начального курса эконометрики, включая имитационное моделирование методом Монте-Карло, могут быть решены с использованием пакета прикладных программ Excel. Решение приводимых в данной книге задач проводится «вручную» с целью отработки соответствующих методов и детального рассмотрения экономического смысла получаемых результатов и выводов. Каждая глава заканчивается вопросами и упражнениями для самопроверки. Знания и навыки, полученные при изучении данного учебного пособия, позволят читателю проводить самостоятельные эконометрические исследования и приступить к освоению компьютерного моделирования.
ВВЕДЕНИЕ
Понятие «эконометрика» введено в 1926 г. норвежским экономистом и статистиком Рагнаром Фришем (лауреат Нобелевской премии по экономике 1969 года «за создание и применение динамических моделей к анализу экономических процессов») и формально означает «измерения в экономике». Область исследований этой науки на современном этапе достаточно широка и продолжает развиваться. Объектами исследований эконометрики являются экономические явления и системы. В отличие от экономической теории, эконометрика делает упор на установление конкретных количественных взаимосвязей между экономическими объектами и показателями. Английский математик и экономист Джеймс Лайтхилл дает короткое и емкое определение: эконометрика – это статистико-математический анализ экономических отношений. Такой подход указывает на естественную связь эконометрики с экономической и математической статистикой. Однако в рамках эконометрики статистические методы являются лишь информационным обеспечением, которое применяется в дальнейшем для анализа экономических взаимосвязей и прогнозирования. Исходя из вышеизложенного, а также опираясь на высказывания признанных авторитетов в области эконометрики (Э. Маленво, Ц. Грилихес, Л. Клейн), можно дать следующее определение, отражающее сущность развития этого научного направления на современном этапе: эконометрика – это наука, в которой на базе реальных статистических данных строятся, анализируются и совершенствуются математические модели экономических процессов. Сущность эконометрики заключается в модельном описании функционирования конкретной экономической системы (экономики данной страны, «спроса-предложения» в данное время в данном месте и т. д.). Одним из основных этапов эконометрических исследований является анализ устойчивости построенной модели, отражающей взаимосвязи между экономическими показателями, и проверка ее на адекватность реальным экономическим данным и процессам. Математическая модель – упрощенное, формализованное представление реального объекта. Наиболее распространенной зависимостью между исследуемой величиной Y и влияющими на нее факторами-аргументами X в экономике является аддитивная линейная форма Y = b 0 + b 1 X 1 + b 2 X 2 + …+ bmXm + ε i, (1) где b 0, b 1, …, bm – некоторые параметры, которые подлежат определению; ε i – остаток, устраняющий разность между модельным (полученным по набору Xj расчетным образом) и наблюдавшимся значениями анализируемой величины Y, обнаруженную в i -м измерении (i = 1, 2 … n; n – общее число измерений). Основная задача эконометрического анализа заключается в отыскании значений параметров b, обеспечивающих наименьшую величину ε,а следовательно, наилучшую точность прогноза. Участвующая в соотношении (1) величина ε i, отражает влияние на результирующий показатель Y всех неучтенных факторов и обусловливает стохастический характер зависимости даже при фиксировании всех переменных X. Таким образом, переходя в своих наблюдениях от одного пространственного (или временного) промежутка к другому, мы увидим случайное варьирование Y около некоторого определенного уровня. Это означает, например, что, зная цену на товар и на конкурирующие с ним или дополняющие товары, а также потребительский доход (факторы), мы не можем сказать однозначно, каким будет спрос на данный товар.
Случайную остаточную составляющую ε i принято называть случайным отклонением. Случайное отклонение ε i является также случайной ошибкой Y по заданным значениям X 1, Х 2, …, Xm. Эконометрические модели (линейные и нелинейные) строятся на основе пространственных данных, которые представляют собой набор экономических переменных, взятых в один и тот же момент времени (пространственный срез), или временных рядов и могут содержать одно или несколько уравнений в зависимости от характера взаимосвязи между экономическими показателями. Основные проблемы эконометрических исследований можно представить в виде следующих этапов: 1. Постановочный этап. Определение и формулировка основных целей модели. Предмодельный анализ экономической ситуации и сущности изучаемого явления. Формирование и обработка информации на основе исходных статистических данных, определение набора возможных факторов и показателей, относящихся к исследуемому объекту. 2. Этап спецификации. Выбор наиболее значимых факторов, участвующих в модели, и математической формы модели, удобной для проведения анализа, т. е. построение самой эконометрической модели. 3. Этап параметризации. Оценка параметров построенной модели на основе имеющихся статистических данных. В решении этой задачи, делающей модель работоспособной, одним из ключевых является вопрос точности используемой статистической информации. 4. Этап верификации. Проверка качества найденных параметров модели и самой модели в целом статистическими методами и сопоставлением модельных и реальных данных. На данном этапе в результате проверки модели на надежность и устойчивость могут быть внесены поправки в задачу спецификации, а именно, откорректирована форма модели и уточнен состав факторов-аргументов. 5. Этап внедрения. Использование построенных моделей для объяснения поведения исследуемых экономических показателей и прогнозирования. Уточнение границ применимости модельного анализа. В последние десятилетия наблюдается стремительное развитие эконометрики как научной дисциплины, в которой используется достаточно тонкий аппарат современной математики. В тоже время, нельзя забывать, что базисом эконометрики является ее экономическая составляющая. Именно экономика определяет постановку задачи и исходные предпосылки, а результат математического моделирования представляет практический интерес лишь в том случае, если удается его экономическая интерпретация. Разработка специальных компьютерных программ, а также совершенствование методов анализа способствуют все более широкому внедрению методов эконометрического моделирования в практические исследования современных социально-экономических процессов.
Нормальное распределение
Нормальный закон распределения (распределение Гаусса) является предельным случаем почти всех реальных распределений вероятности. Поэтому он используется в очень большом числе практических приложений. Непрерывная СВ Х имеет нормальное распределение, если ее плотность вероятности имеет вид:
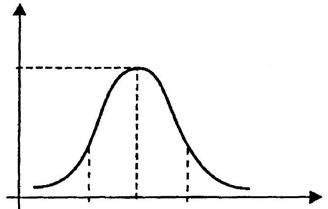
Нормальное распределение (рис. 1.5) полностью определяется двумя параметрами - математическим ожиданием m = M (X) и средним квадратическим отклонением - σ = σ(Х) - и символически обозначается Х ~ N (m, σ2) или X ~ N (m, σ). При изменении числовой характеристики m нормальная кривая перемещается вдоль оси Ох, при изменении σ меняется форма кривой. Нормальный закон распределения с числовыми характеристиками (параметрами) m = 0 и σ2 = 1 называется стандартным распределением.
Рис. 1.5.
Для практических расчетов вероятностей СВ, подчиняющихся нормальному распределению, удобно пользоваться таблицами значений функции Лапласа (Приложение 1). Функция (интеграл вероятностей) Лапласа Ф (u) имеет вид:
где F(u) - функция стандартного нормального распределения СВ U, Р (х 1 £ Х £ х 2) = Ф (u 2) – Ф (u 1), (1.14) где Кроме того, справедливы следующие соотношения: Р (| Х - m | < σ) = 0,68; P(| Х - m | < 2σ) = 0,95; P(| Х - m | < 3σ) = 0,9973, где | Х - m | - отклонение СВ Х от математического ожидания. Другими словами, значения нормально распределенной СВ Х на 95 % сосредоточены в области (m - 2σ, m + 2σ) и на 99,73 % сосредоточены в области (m - 3σ, m + 3σ). Следует также отметить, что линейная комбинация произвольного количества нормальных СВ имеет нормальное распределение. В том случае, когда логарифм СВ подчинен нормальному закону, говорят, что она имеет логарифмически нормальное (логнормальное) распределение.
1.3.2. Распределение χ2 (хи-квадрат)
При моделировании экономических процессов достаточно часто приходится рассматривать СВ, которые представляют собой алгебраическую комбинацию нескольких СВ. Возможность прогнозирования поведения таких СВ осуществляется при использовании ряда специально разработанных законов распределений. К ним относятся χ2-распределение, распределения Стьюдента и Фишера-Снедекора. Пусть имеется n независимых СВ Хi, i = 1, 2 … n, распределенных по нормальному закону, с математическими ожиданиями mi и средними квадратическими отклонениями σ i, соответственно. Если считать, что математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение – единице, тогда СВ Ui = (Xi - mi)/σ i имеют стандартное нормальное распределение, Ui ~ N (0,1). Распределением χ 2 с ν = n степенями свободы называется распределение суммы квадратов n независимых СВ Ui
Число степеней свободы ν исследуемой СВ определяется числом СВ ее составляющих, уменьшенным на число линейных связей между ними. Например, число степеней свободы СВ, являющейся композицией n случайных величин, которые в свою очередь связаны m линейными уравнениями, определяется как ν = n - m. Распределение χ2 определяется одним параметром - числом степеней свободы ν: М (χ2) = ν = n - m, D (χ2) = 2 ν = 2(n - m). График плотности вероятности СВ, имеющей χ2-распределение, расположен только в первой четверти декартовой системы координат и имеет асимметричный вид с вытянутым правым «хвостом». С увеличением числа степеней свободы распределение χ2 постепенно приближается к нормальному распределению. Таблицы критических точек χ2-распределения приведены в Приложении 3.
Распределение Стьюдента
Рассмотрим стандартную нормальную СВ U ~ N (0,1) и независимую от нее СВ V, распределенную по закону χ2 с ν = n степенями свободы (обозначается V ~
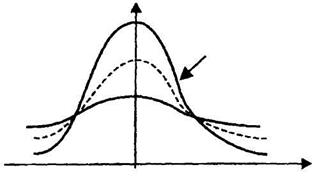
называется распределением Стьюдента (псевдоним английского химика и статистика Госсета) или t -распределением с n -степенями свободы (tn). При n > 2 M (t) = 0 и D (t) = n / n - 2. График функции плотности вероятности СВ, имеющей распределение Стьюдента, является симметричной кривой относительно оси ординат (рис. 1.6) [11].
Рис. 1.6.
С увеличением числа степеней свободы распределение Стьюдента приближается к стандартному нормальному закону и практически при n > 30 можно считать t -распределение приближенно нормальным. Таблица критических точек распределения Стьюдента для различных значений уровня значимости α и числа степеней свободы ν (t α ,ν ) представлена в Приложении 4.
Основные понятия и задачи математической статистики
При исследовании реальных экономических процессов приходится обрабатывать большие объемы статистических данных по самым разнообразным показателям, которые по своей сути являются СВ. Целью таких исследований является получение информации с необходимой степенью достоверности о рассматриваемых объектах, включая установление наличия и степени взаимосвязей между характеризующими их параметрами. Таким образом, основная задача математической статистики состоит в разработке методов сбора, обработки и анализа статистических данных для получения научных и практических выводов. Знание методов математической статистики и умение ими оперировать являются необходимой предпосылкой для успешного эконометрического анализа. В данном разделе приведены основные характеристики и методы анализа статистических данных, которые активно используются в эконометрике.
И выборочные характеристики
При анализе какого-либо экономического показателя Х в фиксированный момент времени (либо без учета фактора времени) наблюдаемые его выборочные значения х 1, х 2, …, хn обычно упорядочивают по возрастанию. Разность между максимальным и минимальным значением СВ Х называется размахом выборки. Пусть количество различных значений в выборке равно k (k £ n). Значения xi, i = 1, 2, …, k называются вариантами выборки. При этом х 1 < x 2 < … < xk. Если значение хi встретилось в выборке ni раз, то число ni называется абсолютной частотой значения хi, а величина
Таблица 1.1
При этом По вариационному ряду можно построить эмпирическую функцию распределения для СВ Х. Эмпирической (выборочной) функцией распределения Fn (x) будем называть относительную частоту (статистическую вероятность) появления события, заключающегося в том, что СВ Х примет значение, меньше указанного х, т. е.: Fn (x) = ω(X < x). (1.29) По определению Fn (x) обладает следующими основными свойствами: 1. 0 £ Fn (х) £ 1. 2. Fn (x) = 0 при Х £ х 1; Fn (x) = 1 при X > xk. Эмпирическая функция распределения Fn (x) является оценкой функции F (x) = P (X < x), которую в этом случае следует называть теоретической функцией распределения. Пример 1.2. Анализируется прибыль Х (%) предприятий отрасли. Обследованы n = 100 предприятий, данные по которым занесены в следующий вариационный ряд [11]:
Необходимо определить эмпирическую функцию распределения Fn (x) и построить ее график.
Рис. 1.7.
При большом объеме выборки ее элементы могут быть сгруппированы в интервальный вариационный ряд. Для этого n наблюдаемых значений выборки х 1, х 2, …, хn разбивают на k непересекающихся интервалов равной ширины h (h – шаг разбиения). Пусть ni – количество наблюдаемых значений СВ Х, попадающих в i -й интервал;
Таблица 1.2
Интервальный вариационный ряд наглядно может быть представлен в виде гистограммы – графика, где по оси абсцисс откладываются интервалы, на каждом из которых строятся прямоугольники с высотой и площадью, пропорциональной относительной частоте попадания СВ Х в данный интервал. На i -м интервале строится прямоугольник высотой Задача (гипотеза) о соответствии теоретического и статистического распределения обычно рассматривается с помощью статистического критерия Пирсона [16], основанного на распределении Поскольку на практике обычно работают с выборкой, нас будут интересовать выборочные числовые характеристики, которые являются оценками соответствующих генеральных характеристик. Если в формуле для математического ожидания дискретной СВ (1.4) положить равными вероятности каждого исхода pi = 1/ n, то получим выборочное среднее арифметическое наблюдаемых значений выборки для СВ Х:
При задании выборки в виде вариационного ряда
Соответственно, для выборочной дисперсии получим формулы:
или (1.32)
Зачастую для вычисления Dв (Х) удобно использовать выражение:
Выборочное среднее квадратическое отклонение определяется как
При задании выборки в виде интервального вариационного ряда в формулах (1.31), (1.32) вместо xi рассматривается среднее значение i -го интервала Выборочный коэффициент вариации Vв будет определяться процентным отношением выборочного среднего квадратического отклонения к выборочному среднему:
Коэффициент вариации – безразмерная характеристика, удобная для сравнения величин рассеивания двух выборок, имеющих различные размерности. Наиболее распространенными характеристиками взаимосвязи двух СВ являются меры их линейной связи – ковариация и коэффициент корреляции (см. раздел 1.4). Их оценками являются выборочная ковариация Covв (X, Y) и выборочный коэффициент корреляции rxy.
Здесь Известно, что если величины X и Y независимы, то выборочный коэффициент корреляции равен нулю; если rxy равен Для нахождения выборочных ковариации и коэффициента корреляции необходимо иметь выборку объема n из двумерной генеральной совокупности (Х, Y), где рассматриваются пары значений xi, yi (i = 1, 2, …, n) в ряду наблюдений. Выборочные оценки числовых характеристик генеральной совокупности обладают теми же основными свойствами, что и их теоретические прототипы.
П.Б. Болдыревский, Зимина С.В.
ЭКОНОМЕТРИКА
Учебное пособие
Нижний Новгород Аннотация Материал учебного пособия разработан на основе лекций, читаемых авторами в течение ряда лет в Нижегородском государственном университете им. Н.И. Лобачевского студентам экономических специальностей. В учебном пособии в концентрированном виде представлена современная методология эконометрического моделирования. Рассмотрены основные элементы эконометрики. Изложены понятия парной, множественной регрессионных моделей, моделей временных рядов и их анализа. Обсуждаются такие вопросы практического многомерного моделирования как гетероскедастичность, мультиколлинеарность, фиктивные переменные, особенности спецификации модели. Учебный материал сопровождается определенным числом вопросов и задач для самопроверки. Для студентов (бакалавриат) экономических специальностей вузов, а также для магистрантов, аспирантов и специалистов, интересующихся методами обработки статистических данных и экономического анализа. ПРЕДИСЛОВИЕ
«Эконометрика» как учебная дисциплина, на современном этапе, благодаря своей универсальности и возможности практического использования для анализа реальных экономических объектов, является одним из базовых курсов в системе высшего экономического образования. В последние годы появились интересные учебники и учебные пособия по эконометрике. Однако, как показывают контакты авторов со студентами, аспирантами, преподавателями и специалистами, занимающимися экономическим анализом, ощущается нехватка доступных учебных пособий по данной дисциплине. В представленном учебном пособии авторами лаконично и на доступном уровне изложены основные вопросы эконометрического анализа, достаточно глубоко и полно рассмотрены базовые понятия эконометрики и регрессионного анализа. Учебное пособие ориентировано на начальный курс эконометрики, и, в первую очередь, предназначено для студентов (бакалавриат) экономических специальностей вузов. Представленный учебный материал направлен на формирование соответствующих профессиональных и общекультурных компетенций. Книга также может быть полезна магистрантам, аспирантам, специалистам и руководителям, изучающим статистические методы анализа экономических процессов и интересующимися прикладными исследованиями в области экономики. Изложение учебного материала предполагает, что читатель владеет основами теории вероятностей, математической статистики и линейной алгебры в объеме курса математики экономического или технического вуза. Пособие состоит из введения, основного учебного материала (главы 1–7) и приложения, содержащего математико-статистические таблицы и методические указания по реализации типовых эконометрических задач на компьютере. В конце книги приведен развернутый предметный указатель основных понятий курса. Во введении рассмотрены основные цели и задачи эконометрики как науки, а также сформулированы основные понятия и этапы эконометрического моделирования. Поскольку основой методов и математического инструментария эконометрики являются теория вероятностей и математическая статистика, в первой главе приведены основные положения этих дисциплин, без которых невозможно понимание материала последующих глав. При этом особое внимание уделяется экономическим приложениям теории вероятностей и математической статистики. В главах 2–7 рассматриваются линейные и сводящиеся к линейным эконометрические модели, как наиболее применимые на практике для анализа и прогнозирования экономических процессов. Для большей наглядности при изложении материала приводятся примеры с решениями. Применение компьютерных пакетов для оценивания эконометрических моделей рассмотрено авторами учебников [25,28, 31]. Многие задачи начального курса эконометрики, включая имитационное моделирование методом Монте-Карло, могут быть решены с использованием пакета прикладных программ Excel. Решение приводимых в данной книге задач проводится «вручную» с целью отработки соответствующих методов и детального рассмотрения экономического смысла получаемых результатов и выводов. Каждая глава заканчивается вопросами и упражнениями для самопроверки. Знания и навыки, полученные при изучении данного учебного пособия, позволят читателю проводить самостоятельные эконометрические исследования и приступить к освоению компьютерного моделирования.
ВВЕДЕНИЕ
Понятие «эконометрика» введено в 1926 г. норвежским экономистом и статистиком Рагнаром Фришем (лауреат Нобелевской премии по экономике 1969 года «за создание и применение динамических моделей к анализу экономических процессов») и формально означает «измерения в экономике». Область исследований этой науки на современном этапе достаточно широка и продолжает развиваться. Объектами исследований эконометрики являются экономические явления и системы. В отличие от экономической теории, эконометрика делает упор на установление конкретных количественных взаимосвязей между экономическими объектами и показателями. Английский математик и экономист Джеймс Лайтхилл дает короткое и емкое определение: эконометрика – это статистико-математический анализ экономических отношений. Такой подход указывает на естественную связь эконометрики с экономической и математической статистикой. Однако в рамках эконометрики статистические методы являются лишь информационным обеспечением, которое применяется в дальнейшем для анализа экономических взаимосвязей и прогнозирования. Исходя из вышеизложенного, а также опираясь на высказывания признанных авторитетов в области эконометрики (Э. Маленво, Ц. Грилихес, Л. Клейн), можно дать следующее определение, отражающее сущность развития этого научного направления на современном этапе: эконометрика – это наука, в которой на базе реальных статистических данных строятся, анализируются и совершенствуются математические модели экономических процессов. Сущность эконометрики заключается в модельном описании функционирования конкретной экономической системы (экономики данной страны, «спроса-предложения» в данное время в данном месте и т. д.). Одним из основных этапов эконометрических исследований является анализ устойчивости построенной модели, отражающей взаимосвязи между экономическими показателями, и проверка ее на адекватность реальным экономическим данным и процессам. Математическая модель – упрощенное, формализованное представление реального объекта. Наиболее распространенной зависимостью между исследуемой величиной Y и влияющими на нее факторами-аргументами X в экономике является аддитивная линейная форма Y = b 0 + b 1 X 1 + b 2 X 2 + …+ bmXm + ε i, (1) где b 0, b 1, …, bm – некоторые параметры, которые подлежат определению; ε i – остаток, устраняющий разность между модельным (полученным по набору Xj расчетным образом) и наблюдавшимся значениями анализируемой величины Y, обнаруженную в i -м измерении (i = 1, 2 … n; n – общее число измерений). Основная задача эконометрического анализа заключается в отыскании значений параметров b, обеспечивающих наименьшую величину ε,а следовательно, наилучшую точность прогноза. Участвующая в соотношении (1) величина ε i, отражает влияние на результирующий показатель Y всех неучтенных факторов и обусловливает стохастический характер зависимости даже при фиксировании всех переменных X. Таким образом, переходя в своих наблюдениях от одного пространственного (или временного) промежутка к другому, мы увидим случайное варьирование Y около некоторого определенного уровня. Это означает, например, что, зная цену на товар и на конкурирующие с ним или дополняющие товары, а также потребительский доход (факторы), мы не можем сказать однозначно, каким будет спрос на данный товар. Случайную остаточную составляющую ε i принято называть случайным отклонением. Случайное отклонение ε i является также случайной ошибкой Y по заданным значениям X 1, Х 2, …, Xm. Эконометрические модели (линейные и нелинейные) строятся на основе пространственных данных, которые представляют собой набор экономических переменных, взятых в один и тот же момент времени (пространственный срез), или временных рядов и могут содержать одно или несколько уравнений в зависимости от характера взаимосвязи между экономическими показателями. Основные проблемы эконометрических исследований можно представить в виде следующих этапов: 1. Постановочный этап. Определение и формулировка основных целей модели. Предмодельный анализ экономической ситуации и сущности изучаемого явления. Формирование и обработка информации на основе исходных статистических данных, определение набора возможных факторов и показателей, относящихся к исследуемому объекту. 2. Этап спецификации. Выбор наиболее значимых факторов, участвующих в модели, и математической формы модели, удобной для проведения анализа, т. е. построение самой эконометрической модели. 3. Этап параметризации. Оценка параметров построенной модели на основе имеющихся статистических данных. В решении этой задачи, делающей модель работоспособной, одним из ключевых является вопрос точности используемой статистической информации. 4. Этап верификации. Проверка качества найденных параметров модели и самой модели в целом статистическими методами и сопоставлением модельных и реальных данных. На данном этапе в результате проверки модели на надежность и устойчивость могут быть внесены поправки в задачу спецификации, а именно, откорректирована форма модели и уточнен состав факторов-аргументов. 5. Этап внедрения. Использование построенных моделей для объяснения поведения исследуемых экономических показателей и прогнозирования. Уточнение границ применимости модельного анализа. В последние десятилетия наблюдается стремительное развитие эконометрики как научной дисциплины, в которой используется достаточно тонкий аппарат современной математики. В тоже время, нельзя забывать, что базисом эконометрики является ее экономическая составляющая. Именно экономика определяет постановку задачи и исходные предпосылки, а результат математического моделирования представляет практический
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.115.79 (0.014 с.) |

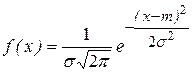 . (1.12)
. (1.12)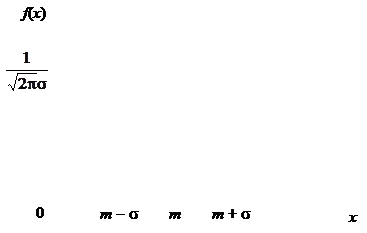
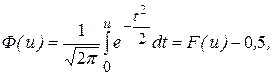 (1.13)
(1.13)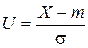 . Тогда вероятность попадания СВ Х, распределенной по нормальному закону, в интервал [ х 1, х 2].
. Тогда вероятность попадания СВ Х, распределенной по нормальному закону, в интервал [ х 1, х 2].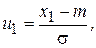
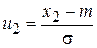 .
.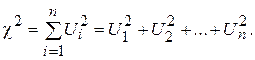 (1.15)
(1.15)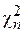 ). Тогда распределение случайной величины
). Тогда распределение случайной величины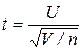 (1.16)
(1.16)
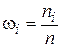 – относительной частотой значения хi. Тогда наблюдаемые выборочные значения можно представить в виде вариационного (статистического) ряда (табл. 1.1).
– относительной частотой значения хi. Тогда наблюдаемые выборочные значения можно представить в виде вариационного (статистического) ряда (табл. 1.1).

 …
… 
 ,
,  .
.



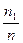


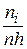 . На основании гистограммы обычно выдвигают предположение о виде закона распределения исследуемой СВ Х.
. На основании гистограммы обычно выдвигают предположение о виде закона распределения исследуемой СВ Х. (Приложение 6).
(Приложение 6). . (1.30)
. (1.30) . (1.31)
. (1.31)
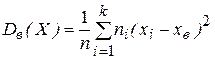 .
. . (1.33)
. (1.33) . (1.34)
. (1.34) .
. . (1.35)
. (1.35) , (1.36)
, (1.36)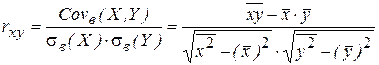 . (1.37)
. (1.37) .
. , то Y и X связаны линейной функциональной зависимостью [16].
, то Y и X связаны линейной функциональной зависимостью [16].


