
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
События. Действия с событиямиСодержание книги
Поиск на нашем сайте
Определение. Элементарным событием называется простейший неделимый исход некоторого опыта. Элементарные исходы будем обозначать символом Определение. Пространством элементарных исходов называется множество всех элементарных исходов, которое будем обозначать символом Рассмотрим несколько примеров. Пример 1. Описать пространствоэлементарных исходов при подбрасывании монеты. m Решение. Очевидно, что при подбрасывании монеты возможны два элементарных исхода:
Таким образом, пространство элементарных исходов содержит два элемента
Пример 2. Описать пространствоэлементарных исходов при подбрасывании игрального кубика. m Решение. Очевидно, что при подбрасывании игрального кубика элементарными исходами является число, выпавших очков, т.е.
Таким образом, пространство элементарных исходов содержит шесть элементов
Пример 3. На отрезке m Решение. В этом случае результатом является координата
Пространствоэлементарных исходов имеет бесконечно много элементов. l Определение. Событие называется достоверным, если в результате опыта оно непременно должно произойти. Достоверное событие обозначают символом Определение. Событие называется невозможным, если в результате опыта оно не может произойти. Невозможное событие обозначают символом Определение. События Так, например, если при бросании игральной кости выпала грань «2», то это означает, что при том же бросании не могла появиться грань «4». Определение. События
Например, при однократном бросании игральной кости полная группа попарно несовместимых событий состоит из событий
которые состоят соответственно в выпадении 1,2,3,4,5,6 очков соответственно. Наряду с элементарными событиями будем рассматривать случайные события. Определение. Случайным событием Определение. Элементарные события, принадлежащие подмножеству Рассмотрим основные операции над событиями; они полностью соответствуют основным операциям над множествами. Определение. Суммой событ ий Элементарными исходами суммы событий Определение. Произведением событий Элементарными исходами произведения событий Определение. Разностью событий Элементарными исходами разности событий Определение. Событие, состоящее в том, что событие Элементарными исходами противоположного события Определение. Событие Определение. Если одновременно Пример 4. Если
Свойства операций над событиями: § § § § § § § § §
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.195.30 (0.008 с.) |

 .
. .
. — появление «герба»;
— появление «герба»; — появление «решки».
— появление «решки». . l
. l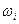 — выпало ровно
— выпало ровно 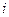 очков;
очков;  .
. или
или  . l
. l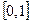 случайным образом отмечается точка. Описать пространствоэлементарных исходов.
случайным образом отмечается точка. Описать пространствоэлементарных исходов. , удовлетворяющая условию
, удовлетворяющая условию  . Очевидно, что координата
. Очевидно, что координата 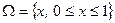 .
. . Событие, состоящее в появлении 7 очков при бросании игрального кубика, является невозможным.
. Событие, состоящее в появлении 7 очков при бросании игрального кубика, является невозможным. называют несовместными, если при наступлении одного из событий, остальные
называют несовместными, если при наступлении одного из событий, остальные  события в данном испытании наступить уже не могут.
события в данном испытании наступить уже не могут. ,
, (или просто событием
(или просто событием  называется событие
называется событие 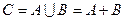 , состоящее в наступлении хотя бы одного из событий
, состоящее в наступлении хотя бы одного из событий  являются элементарные исходы, принадлежащие хотя бы одному из событий
являются элементарные исходы, принадлежащие хотя бы одному из событий 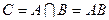 , состоящее в совместном (одновременном) наступлении этих событий.
, состоящее в совместном (одновременном) наступлении этих событий. являются те элементарные исходы, которые одновременно принадлежат событиям
являются те элементарные исходы, которые одновременно принадлежат событиям 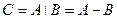 , состоящее в том, что событие
, состоящее в том, что событие  являются те элементарные исходы события
являются те элементарные исходы события  .
.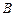 (
(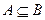 .
. , то в этом случае события
, то в этом случае события  .
.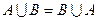 ,
, 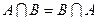 (коммутативность);
(коммутативность); ,
, 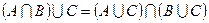 (дистрибутивность);
(дистрибутивность); ,
,  (ассоциативность);
(ассоциативность);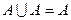 ,
, 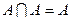 ;
; ,
,  ;
;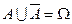 ,
,  ;
; ,
,  ,
, 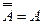 ;
;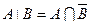 ;
; ,
,  (законы де Моргана).
(законы де Моргана).


