
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие испытания. Простр-во элементарных событий.Содержание книги
Поиск на нашем сайте
Понятие испытания. Простр-во элементарных событий. Неопределенными понятиями в теор. вероятностей является испытание(опыт, наблюдение, эксперимент) и элементарное событие(элементарный исход). Под испытанием понимается реализация определен. комплекса условий, в рез-те которых наступает ровно 1 элементарн. событие из общей совокупности, называемой простр-вом элементарных событий. Ω = {w1,w2,w3,…} – простр-во элементарн. событий; wi – элементарное событие. В зависимости от числа элементарн. событий в простр-ве различают конечное, счетное, несчетное простр-во элементарн. событий. Конечное простр-во содержит конечное число элементарн. событий. Счетное – бесконечное число, но такое, кот. можно пересчитать. Несчетное простр-во содержит бесконечное число элементарн. событий не поддающихся нумерации.
Определение событий. Виды событий. Действия над событиями. Событием (или случайным событием) называется любое подмнож-во простр-ва элементарн. событий, если оно конечно или счетно. Определ.: события называются эквивалентными, если они состоят из одних и тех же элементарн. событий. Эквивалентные события наступают или не наступают одновременно. Опред.: Событие назыв. невозможным, если оно не содержит ни одного элементарн. события. Невозможное событие никогда не происходит. Опред.: Событие назыв. достоверным, если оно содержит все элементарн. события простр-ва Ω. Достоверное событие происходит при каждом испытании. Введем операции над событиями: Суммой событий А и В назовем событие А+В, состоящее из элементарн. событий принадлежащих или событию А, или соб. В. А+В = {w: w
Статистическая вероятность Классическое определение вероятности предполагает, что число элементарн. исходов испытания конечно. На практике часто встречаются испытания, число возможных исходов кот. бесконечно. В таких случаях классическое определение неприменимо. Наряду с классич. определением используют статистич. определение. В кач-ве статистич. вероятности события принимают относительн. частоту или число близкое к ней. Св-ва вероятности, вытекающие из классич. определения сохраняются и при статистич. определ. Если событие достоверно, то его относит. частота =1, т.е. статистич. вероятность также =1. Если событие невозможно, то относит. частота = 0, т.е. статист. вероятность тоже =0. Для любого события 0£W(A)£ 1, следоват. статистич. вероятность заключена между 0 и 1. Для существования статист. вероятности требуется: 1) возможность хотя бы принципиально проводить неограничен. число испытаний, в каждом из кот. событие наступает или не наступает; 2) устойчивость относит. частоты появления события в различных сериях достаточно большого числа испытаний. Недостатком статистич. определения является неоднозначность статистич. вероятности. Напр., если в рез-те достаточно большого числа испытаний оказалось, что относит. частота весьма близка к 0,6, то это число можно принять за статистич. вероятность. Но в кач-ве вероятности события можно принять не только 0,6, но и 0,59 и 0,61.
Геометрическая вероятность Чтобы преодолеть недостаток классич. определения вероятности, состоящий в том, что оно не применимо к испытаниям с бесконечным числом исходов, вводят геометрич. вероятности, т.е. вероятности попадания точки в область, на отрезок, часть плоскости и т.д. Пусть отрезок длины l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: Поставлен. точка может оказаться в любой точке отрезка L. Вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. P=длина l/длина L. Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Это означает выполнение следующ. предположений: Брошенная точка может оказаться в любой точке фигуры G. Вероятность попадания брошен. точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы фигуры g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством: P= площадь g/площадь G.
Понятие об алгебре событий Построим матем. модель, в кот. учитывались бы все возможные исходы эксперимента. Пусть Ω – производное пространство элементарн. событий, а F – некоторый класс подмнож-в множества Ω. Класс подмнож-в F называется алгеброй событий, если выполняются следующ. условия: 1)ΩÎF; 2)AÇBÎF, AÈBÎF, A-BÎF; "A,BÎF; 3)AÎF, тогда ĀÎF. Если задано множ-во W и какая-нибудь s-алгебра F, то говорят, что задано измеримое пространство(обозначается <W,F>). Для того, чтобы формализовать какую-нибудь вероятностн. задачу, надо соответствующ. эксперименту приписать измеримое пространство <W,F>, где W обозначает множ-во элементарн. исходов эксперимента, а s-алгебра F определяет класс событий, среди кот. находятся и интересующие.
Аксиомы Колмогорова Числовая функция Р, определенная на классе событий F называется вероятностью, если выполняются следующ. условия: Аксиома 1. F является алгеброй событий; Аксиома 2. Р(А)³0 для любого АÎF; Аксиома 3. Р(W)=1; Аксиома 4. Если А,В – несовместные события, то Р(А+В)=Р(А)+Р(В). Для решения задач, связанных с бесконечн. последовательностями событий, требуется дополнить приведен. аксиомы следующ. аксиомой непрерывности: Аксиома 5. Для любой убывающей последоват-и событий из F такой, что произведение этих событий есть невозможн. событие, справедливо равенство: lim(при x→∞) P(An)=0, т.е. А1 Эти аксиомы называются аксиомами Колмогорова.
Формула полной вероятности Пусть требуется определить вер. некотор. события А, кот. может произойти вместе с одним из событий H1,H2,…,Hn, образующ. полную группу несовместн. событий. События H1,H2,…,Hn будем называть гипотезами. Докажем, что в этом случае P(A) вычисляется как
Формула Байеса Следствиеь теоремы умножения и формулы полной вер. явл. теорема гипотез или формула Байеса. Поставим след. задачу: имеется полная группа несовместн. гипотез H1,H2,…,Hn. Вероятности этих гипотез до опыта известны и равны P(H1), P(H2),…, P(Hn). Произведен опыт, в рез-те кот. появилось некотор. событие А. Как следует изменить вероятности гипотез в связи с появлением этого события? Т.е. нужно найти условн. вер. PA(Hi) для каждой гипотезы. Из теоремы умножения вероятностей: P(AHi)=P(A)
Формула Бернулли При решении вероятностн. задач часто приходится сталкиваться с ситуациями, в кот. одно и тоже испытание повторяется многократно. В рез-те каждого опыта может появиться или не появиться некотор. соб. А, причем нас интересует не рез-т каждого отдельного опыта, а общее число появлений соб. А в рез-те серии опытов. Модель рассматрив. ситуации выглядит след. образом: проводится n испытаний, в каждом из кот. соб. А может произойти или нет. Причем вероятность события в кажд. отдельн. испытании постоянна, т.е. не меняется от испытания к испытанию. Требуется определить вер. m появлений соб. А в n испытаниях. Подобн. задачи решаются довольно легко, если испытания явл. независимыми. Опред.: Неск-ко испытаний назыв. независим. относит-но соб. А, если вер. соб. А в кажд. из них не зависит от исходов др. испытаний. Напр, неск-ко последоват. бросаний монет представляют собой независим. опыты. Производится n независим. опытов, в кажд. из кот. может появиться или не появ. некотор. соб.А. Вер. появл. данного события в кажд. опыте постоянна и равна p, а вер. непоявления=q. Требуется найти вер. Pn(m) того, что соб. А в этих n опытах появится m раз. Рассмотрим событие Bm, состоящ. в том, что соб. А появится в этих n опытах ровно m раз. Разложим соб. Bm на сумму произведен. событий, состоящих в появлении или непоявл. соб. А в определ. опыте. Каждый вар-т появл. соб. Bm должен состоять из m появлений соб. А или n-m непоявл. соб. А. Bm=А1А2…Аm
Формула Пуассона Если вер. события p в отдельн. испытании близка к 0, то даже при большом числе испытаний n, но небольш. величине
Закон Пуассона ДСВ Х, кот. может принимать только целые неотрицат. значения с вероятностями Pm = P(X=m) =
Определение закона Пуассона корректно, т.к. 37. Показательное распределение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной СВ Х, которое описывается функцией плотности вероятности Определим числовые хар-ки СВ, распределенной по показательному закону. Матем. ожидание: M(X) =
Неравенство Чебышева. Нер-во Чебышева относится к группе «закона больших чисел». Пусть имеется СВ Х с мат. ожиданием mx и Dx. Нер-во Чебышева утверждает, что, каково бы ни было положительное число α, вероятность того, что величина Х отклонится от своего мат. ожидания не меньше чем на α, ограничена сверху величиной Dx/ α2: P(|X - mx |≥α)≤ Dx/ α2. Доказ-во: Пусть величина Х прерывная, с рядом распределения:
Изобразим возможные значения величины Х и ее мат. ожидание mx в виде точек на числовой оси Ox. Зададим некоторым значением α>0 и вычислим вероятность того, что величина Х отклонится от своего мат. ожидания не меньше, чем на α: P(|X - mx |≥α) – формула (1). Для этого отложим от точки mx вправо и влево по отрезку длиной α; получим отрезок АВ. Вероятность (1) есть не что иное, как вероятность того, что случайная точка Х попадет не внутрь отрезка АВ, а вовне его: P(|X - mx |≥α) = P(X
Понятие испытания. Простр-во элементарных событий. Неопределенными понятиями в теор. вероятностей является испытание(опыт, наблюдение, эксперимент) и элементарное событие(элементарный исход). Под испытанием понимается реализация определен. комплекса условий, в рез-те которых наступает ровно 1 элементарн. событие из общей совокупности, называемой простр-вом элементарных событий. Ω = {w1,w2,w3,…} – простр-во элементарн. событий; wi – элементарное событие. В зависимости от числа элементарн. событий в простр-ве различают конечное, счетное, несчетное простр-во элементарн. событий. Конечное простр-во содержит конечное число элементарн. событий. Счетное – бесконечное число, но такое, кот. можно пересчитать. Несчетное простр-во содержит бесконечное число элементарн. событий не поддающихся нумерации.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.77 (0.011 с.) |

 A или w
A или w 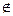 B}. Определ.: События назыв. противоположными, если кажд. из них содержит те элементарн. события, кот. не содержит другое событие. Если А – некоторое событие, то противоположн. ему событие Ā, причем оно единственное. Если событие произошло, то противоположное ему событие не произошло, и наоборот. Ā = {w
B}. Определ.: События назыв. противоположными, если кажд. из них содержит те элементарн. события, кот. не содержит другое событие. Если А – некоторое событие, то противоположн. ему событие Ā, причем оно единственное. Если событие произошло, то противоположное ему событие не произошло, и наоборот. Ā = {w  А2
А2  ;
; 
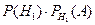 +
+  +…+
+…+  =
=  . Т.е. P(A) вычисляется как сумма произведений вероятности каждой гипотезы на соответств. условн. вер. события А. Доказ-во: Т.к. гипотезы H1,H2,…,Hn образуют полную группу, то соб. А может появиться в комбинации с какой-л. из этих гипотез, т.е. A=H1A+H2A+…+HnA. Т.к. гипотезы H1,H2,…,Hn несовместны, то и комбинации H1A,H2A,…,HnA несовместны. Применяя теорему сложения, получаем P(A)= P(H1A)+P(H2A)+…+P(HnA). Применяя к событию HiA теорему умножения вероятностей, получаем P(A)=
. Т.е. P(A) вычисляется как сумма произведений вероятности каждой гипотезы на соответств. условн. вер. события А. Доказ-во: Т.к. гипотезы H1,H2,…,Hn образуют полную группу, то соб. А может появиться в комбинации с какой-л. из этих гипотез, т.е. A=H1A+H2A+…+HnA. Т.к. гипотезы H1,H2,…,Hn несовместны, то и комбинации H1A,H2A,…,HnA несовместны. Применяя теорему сложения, получаем P(A)= P(H1A)+P(H2A)+…+P(HnA). Применяя к событию HiA теорему умножения вероятностей, получаем P(A)=  PA(Hi)=P(Hi)
PA(Hi)=P(Hi)  ,
,  ; PA(Hi)=
; PA(Hi)= 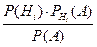 ,
,  ,
,  …
…  . Каждое произведен. соб. А должно происходить m раз, а
. Каждое произведен. соб. А должно происходить m раз, а 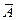 n-m раз. Число всех комбинаций такого рода равно
n-m раз. Число всех комбинаций такого рода равно  , т.е. равно числу способов, какими можно из n опытов выбрать m, в кот. произошло соб. А. Вер. каждой такой комбинации по теор. умножен. для независ. событий равна
, т.е. равно числу способов, какими можно из n опытов выбрать m, в кот. произошло соб. А. Вер. каждой такой комбинации по теор. умножен. для независ. событий равна  . Т.к. комбинации между собой несовместны, то по теор. сложения вер. соб. Bm равна
. Т.к. комбинации между собой несовместны, то по теор. сложения вер. соб. Bm равна  . Т.о., если производится n независим. опытов, в кажд. из кот. соб. А появляется с вер. p, то вер. того, что соб. А появится ровно m раз, выражается формулой
. Т.о., если производится n независим. опытов, в кажд. из кот. соб. А появляется с вер. p, то вер. того, что соб. А появится ровно m раз, выражается формулой 
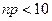 вероятности
вероятности  , получен. по локальн. формуле Лапл. не достаточно близки к их истин. значениям. В таких случаях применяют формулу Пуасона. Теор.: Если вер. p наступления соб. А в кажд. испытании постоянна, но близка к 0, число независим. испытаний n достаточн. велико, а
, получен. по локальн. формуле Лапл. не достаточно близки к их истин. значениям. В таких случаях применяют формулу Пуасона. Теор.: Если вер. p наступления соб. А в кажд. испытании постоянна, но близка к 0, число независим. испытаний n достаточн. велико, а  , то вер.
, то вер.  . Это формула Пуасона. Доказ-во: Для вычисления вер.
. Это формула Пуасона. Доказ-во: Для вычисления вер.  (Т.к.
(Т.к.  )=
)=  . Т.к. по условию n велико, то найдем предел правой части последн. равенства при
. Т.к. по условию n велико, то найдем предел правой части последн. равенства при  , при этом будет получено приближен. значение вероятн.:
, при этом будет получено приближен. значение вероятн.: 
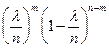 =
= 

 =
= 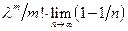

 =
=  Пределы всех скобок, кроме предпоследн. равны 1 при
Пределы всех скобок, кроме предпоследн. равны 1 при  . Замечание: Формулу Пуассона обычно используют, когда
. Замечание: Формулу Пуассона обычно используют, когда  , а
, а  , называется распределенной по закону Пуассона с параметром распределения λ, где λ=np. В отличие от биномиальн. распределения здесь СВ может принимать бесконечное мн-во значений, представляющ. собой бесконечн. последовательность целых чисел(0, 1, 2, 3, … и т.д.). Закон Пуассона описывает число событий m, происходящ. за одинаковые промежутки времени. При этом полагается, что события появляются независимо друг от друга с постоянной средней интенсивностью, кот. характеризуется параметром λ=np. Ряд распределения закона Пуассона имеет вид:
, называется распределенной по закону Пуассона с параметром распределения λ, где λ=np. В отличие от биномиальн. распределения здесь СВ может принимать бесконечное мн-во значений, представляющ. собой бесконечн. последовательность целых чисел(0, 1, 2, 3, … и т.д.). Закон Пуассона описывает число событий m, происходящ. за одинаковые промежутки времени. При этом полагается, что события появляются независимо друг от друга с постоянной средней интенсивностью, кот. характеризуется параметром λ=np. Ряд распределения закона Пуассона имеет вид: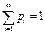 выполнена. Действительно функцию ex можно разложить в ряд, кот. сходится для любого Х. Поэтому eλ =
выполнена. Действительно функцию ex можно разложить в ряд, кот. сходится для любого Х. Поэтому eλ =  = 1+ λ + λ2/2! + …+ λm/m! +… Тогда
= 1+ λ + λ2/2! + …+ λm/m! +… Тогда  = e—λ
= e—λ  = e—λ eλ =1. Найдем мат. ожидание и дисперсию СВ Х, распределенной по закону Пуассона. M(X) =
= e—λ eλ =1. Найдем мат. ожидание и дисперсию СВ Х, распределенной по закону Пуассона. M(X) =  =
=  =
=  = λ e—λ
= λ e—λ  = λe—λ eλ = λ = np. Суммирование начинается с m=1, т.к. 1-ый член суммы соответствующий m=0 равен 0. Дисперсию СВ Х найдем по формуле D(X) = M(X2) – (M(X))2. M(X2) =
= λe—λ eλ = λ = np. Суммирование начинается с m=1, т.к. 1-ый член суммы соответствующий m=0 равен 0. Дисперсию СВ Х найдем по формуле D(X) = M(X2) – (M(X))2. M(X2) =  = e—λ
= e—λ  = e—λ
= e—λ  = λ2 e—λ
= λ2 e—λ  + λ e—λ
+ λ e—λ  = λ2 e—λ eλ + λ e—λ eλ = λ2 +λ. Тогда D(X) = λ2 +λ — λ2 = λ = np. Т.о. мат. ожидание и дисперсия СВ, распределенной по закону Пуассона, совпадают и равны параметру этого распределения λ.
= λ2 e—λ eλ + λ e—λ eλ = λ2 +λ. Тогда D(X) = λ2 +λ — λ2 = λ = np. Т.о. мат. ожидание и дисперсия СВ, распределенной по закону Пуассона, совпадают и равны параметру этого распределения λ. , где λ>0 постоянна и называется параметром показательного распределения. Примером непрерывн. СВ, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока, где λ – интенсивность потока. Найдем функцию распределения F(x) СВ, распределенной по показательному закону: F(x) =
, где λ>0 постоянна и называется параметром показательного распределения. Примером непрерывн. СВ, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока, где λ – интенсивность потока. Найдем функцию распределения F(x) СВ, распределенной по показательному закону: F(x) = 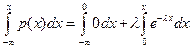 =
=  . Итак,
. Итак, 
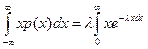 =
=  =
=  . Дисперсия: D(X) =
. Дисперсия: D(X) = 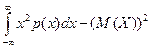 =
=  = 2/λ2 – 1/λ2 = 1/λ2. Среднеквадратическое отклонение σ(Х) = 1/λ и, следовательно, совпадает с мат. ожиданием.
= 2/λ2 – 1/λ2 = 1/λ2. Среднеквадратическое отклонение σ(Х) = 1/λ и, следовательно, совпадает с мат. ожиданием. AB). Для того, чтобы найти эту вероятность, нужно просуммировать вероятности всех тех значений Х, которые лежат вне отрезка АВ. Запишем это следующим образом: P(|X - mx |≥α) =
AB). Для того, чтобы найти эту вероятность, нужно просуммировать вероятности всех тех значений Х, которые лежат вне отрезка АВ. Запишем это следующим образом: P(|X - mx |≥α) =  - формула (2), где запись |X - mx |≥α под знаком суммы ознаачет, что суммирование распространяется на все те значения, для которых точки Х лежат вне отрезка АВ. С другой стороны напишем выражение дисперсии величины Х: D(X) = M[(X - mx)2] =
- формула (2), где запись |X - mx |≥α под знаком суммы ознаачет, что суммирование распространяется на все те значения, для которых точки Х лежат вне отрезка АВ. С другой стороны напишем выражение дисперсии величины Х: D(X) = M[(X - mx)2] =  - формула (3). Т.к. все члены суммы (3) неотрицательны, она может только уменьшиться, если мы распространим ее не на все значения Х, а только на некоторые, в частности на те, котрые лежат вне отрезка АВ: D(X) ≥
- формула (3). Т.к. все члены суммы (3) неотрицательны, она может только уменьшиться, если мы распространим ее не на все значения Х, а только на некоторые, в частности на те, котрые лежат вне отрезка АВ: D(X) ≥ 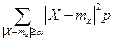 . Заменим под знаком суммы выражение |X - mx | через α. Т.к. для всех членов суммы |X - mx |≥α, то от такой замены сумма тоже может уменьшится; значит, D(X) ≥
. Заменим под знаком суммы выражение |X - mx | через α. Т.к. для всех членов суммы |X - mx |≥α, то от такой замены сумма тоже может уменьшится; значит, D(X) ≥  . Но согласно формуле (2) сумма, стоящая в правой части последнего рав-ва есть не что иное, как вероятность попадания случайной точки вовне отрезка АВ; следовательно, D(X) ≥ α2P(|X - mx |≥α), откуда непостредственно вытекает доказываемое нер-во. В случае, когда величина Х непрерывна, доказ-во проводится аналогичным образом с заменой вероятностей p элементом вероятности, а конечных сумм – интегралами. Действительно, P(|X - mx |>α) =
. Но согласно формуле (2) сумма, стоящая в правой части последнего рав-ва есть не что иное, как вероятность попадания случайной точки вовне отрезка АВ; следовательно, D(X) ≥ α2P(|X - mx |≥α), откуда непостредственно вытекает доказываемое нер-во. В случае, когда величина Х непрерывна, доказ-во проводится аналогичным образом с заменой вероятностей p элементом вероятности, а конечных сумм – интегралами. Действительно, P(|X - mx |>α) =  , где f(x) – плотность распределения величины Х. Далее, имеем: D(X) =
, где f(x) – плотность распределения величины Х. Далее, имеем: D(X) = 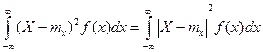 ≥
≥  , где знак |X - mx |>α под интегралом означает, что интегрирование распространяется на внешнюю часть отрезка АВ. Заменяя |X - mx | под знаком интеграла через α, получим: D(X) ≥ α2
, где знак |X - mx |>α под интегралом означает, что интегрирование распространяется на внешнюю часть отрезка АВ. Заменяя |X - mx | под знаком интеграла через α, получим: D(X) ≥ α2 


