Закон распределения функции двух СВ.

Задача определения закона распределения функции нескольких случайных аргументов значительно сложнее аналогичной задачи для функции одного аргумента.

Имеется система двух непрерывных СВ (X, Y) с плотностью распределения f(x, y). Случайная величина Z связана с X и Y функцианальной зависимостью: Z = φ(X, Y). Требуется найти закон распределения величины Z. Функция z = φ(x, y) изображается поверхностью, а не кривой, как в случае одного аргумента. Найдем функцию распределения величины Z: G(z) = P(Z<z) = P(φ(X, Y)<z) – формула (1). Проведем плоскость Q, параллельную плоскости xOy, на расстоянии z от нее. Эта плоскость пересечет поверхность z = φ(x, y) по некоторой кривой K. Спроектируем кривую К на плоскость xOy. Эта проекция, уравнение которой φ(x, y) = z, разделит плоскость xOy на две области; для одной из них высота поверхности над плоскостью xOy будет меньше, а для другой – больше z. Обозначим D ту область, для которой эта высота меньше z. Чтобы выполнялось неравенство (1), случайная точка (X, Y), очевидно, должна попасть в область D; следовательно, G(z) = P((X,Y) D) = - формула (2). В выражение (2) величина z входит неявно, через пределы интегрирования. Дифференцируя G(z) по z, получим плотность распределения величины Z: g(z) = G'(z). Зная конкретный вид функции z = φ(x, y), можно выразить пределы интегрирования через z и написать выражение g(z) в явном виде. Для того, чтобы найти закон распределения функции двух аргументов, нет необходимости каждый раз строить поверхность z = φ(x, y) и пересекать ее плоскостью, параллельной xOy. На практике достаточно построить на плоскости xOy кривую, уравнение которой z = φ(x, y), отдать себе отчет, по какую сторону этой кривой Z<z, а по какую Z>z, и интегрировать по области D, для которой Z<z.

 

 

41. Понятие закона больших чисел.

Содержание закона больших чисел в широком смысле: при очень большом числе случайных явлений средний их рез-т практически перестает быть случайным и может быть предсказан с большой степенью определенности. В узком смысле слова под законом больших чисел в теории вероятностей понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным. Простейшей из этих теорем является теорема Бернулли. Она утверждает, что при большом числе опытов частота события приближается (точнее – сходится по вероятности) к вероятности этого события. Другие, более общие формулировки, устанавливабт факт и условия сходимости по вероятности тех или иных СВ к постоянным, не случайным величинам. Закон больших чисел играет важную роль в практических применениях теории вероятности. Св-во случайных величин при определенных условиях вести себя практически как не случайные позволяет уверенно оперировать с этими величинами, предсказывать рез-ты массовых случайных явлений (это большое число выполняемых однородных опытов или большое число складывающихся случайных воздействий, порождающих в своей совокупности случайную величину, подчиненную вполне определенному закону) почти с полной опреленностью.

 

 

Неравенство Чебышева.

Нер-во Чебышева относится к группе «закона больших чисел».

Пусть имеется СВ Х с мат. ожиданием m_x и D_x. Нер-во Чебышева утверждает, что, каково бы ни было положительное число α, вероятность того, что величина Х отклонится от своего мат. ожидания не меньше чем на α, ограничена сверху величиной D_x/ α²: P(|X - m_x |≥α)≤ D_x/ α². Доказ-во: Пусть величина Х прерывная, с рядом распределения:

Х	x1	x2	…	xn
p	p1	p2	…	pn

Изобразим возможные значения величины Х и ее мат. ожидание m_x в виде точек на числовой оси Ox. Зададим некоторым значением α>0 и вычислим вероятность того, что величина Х отклонится от своего мат. ожидания не меньше, чем на α: P(|X - m_x |≥α) – формула (1). Для этого отложим от точки m_x вправо и влево по отрезку длиной α; получим отрезок АВ. Вероятность (1) есть не что иное, как вероятность того, что случайная точка Х попадет не внутрь отрезка АВ, а вовне его: P(|X - m_x |≥α) = P(X AB). Для того, чтобы найти эту вероятность, нужно просуммировать вероятности всех тех значений Х, которые лежат вне отрезка АВ. Запишем это следующим образом: P(|X - m_x |≥α) = - формула (2), где запись |X - m_x |≥α под знаком суммы ознаачет, что суммирование распространяется на все те значения, для которых точки Х лежат вне отрезка АВ. С другой стороны напишем выражение дисперсии величины Х: D(X) = M[(X - m_x)²] = - формула (3). Т.к. все члены суммы (3) неотрицательны, она может только уменьшиться, если мы распространим ее не на все значения Х, а только на некоторые, в частности на те, котрые лежат вне отрезка АВ: D(X) ≥ 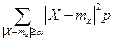. Заменим под знаком суммы выражение |X - m_x | через α. Т.к. для всех членов суммы |X - m_x |≥α, то от такой замены сумма тоже может уменьшится; значит, D(X) ≥ . Но согласно формуле (2) сумма, стоящая в правой части последнего рав-ва есть не что иное, как вероятность попадания случайной точки вовне отрезка АВ; следовательно, D(X) ≥ α²P(|X - m_x |≥α), откуда непостредственно вытекает доказываемое нер-во. В случае, когда величина Х непрерывна, доказ-во проводится аналогичным образом с заменой вероятностей p элементом вероятности, а конечных сумм – интегралами. Действительно, P(|X - m_x |>α) = , где f(x) – плотность распределения величины Х. Далее, имеем: D(X) = 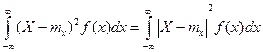≥ , где знак |X - m_x |>α под интегралом означает, что интегрирование распространяется на внешнюю часть отрезка АВ. Заменяя |X - m_x | под знаком интеграла через α, получим: D(X) ≥ α² = α²P(|X - m_x |>α), откуда и вытекает нер-во Чебышева для непрерывных величин.