
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства арифметической средней величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Если a=const, то 2. Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю: 3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа: 4. Если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число, то и средняя величина возрастет или уменьшится на столько же, т.е происходит сдвиг по оси абсцисс: 5. Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшится во столько же раз:
6. Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится: Следствие 1. (из 6) Вместо абсолютных значений весов можно использовать доли или проценты. Следствие 2. Если все веса равны, то средняя арифметическая простая равна средней арифметической взвешенной. Правила выбора средней. § Средняя арифметическая используется, если известны численные значения знаменателя формулы, а значение числителя могут быть получены произведением. Например, известна з/п каждого рабочего в цехе и количество работников, нужно определить среднюю з/п по цеху. § Средняя гармоническая используется, если известны числовые значения числителя, а значения знаменателя могут быть получены как частные от деления показателя. Например, известно xi – курс акций i-того эмитента, fi – стоимость акций i-того эмитента, нужно определить средний курс акций. § Средняя геометрическая применяется, если необходимо найти значение признака, качественно равноудаленного от максимального и минимального значений. Например, известны максимальный и минимальный выигрыши в лотерею, нужно определить средний выигрыш. § Средняя квадратическая применяется для измерения вариации признаков совокупности, что обусловлено 3 свойством средней арифметической. § Средняя хронологическая используется, если данные представлены не за какой-либо период, и по состоянию на дату:
Существуют структурные средние или структурные величины, которые характеризуют структуру совокупности. К ним относятся мода и квантили. Мода – значение признака, чаще всего встречающегося в совокупности или варианта, имеющая наибольшую частоту. Если мод несколько, то совокупность является неоднородной. Для дискретного ряда ищется варианта с максимальной частотой. Для интервального ряда сначала определяется модальный интервал, т.е. интервал с максимальной частотой, а затем ищется мода по следующей формуле:
где x0 – нижняя граница модального интервала; h – величина модального интервала;
Квантиль - это значение признака, делящее ряд в некотором отношении (как правило, на равные части). Формальное определение звучит следующим образом: это значение хq случайной величины, удовлетворяющей условию: F(xq) = q, где F(xq) = (X<x). В основном используют следующие виды квантилей: § медиану при q=0.5 § квартили при q=0.25 § квинтили при q=0.2 § децили при q=0.1 § перцентили при q=0.01 Для дискретного ряда
где x0i – нижняя граница квантильного интервала; h – величина квантильного интервала;
Подставляя различные Квантили используется для расчета показателей, концентрации и дифференциации доходов населения. По данным выборочных опросов получают интервальный ряд распределения населения по среднедушевому доходу. Расчет коэффициента концентрации Джини производится на основании данных о распределении населения по уровню среднедушевого совокупного дохода. Вся совокупность получателей доходов делится на 5 равных групп и определяется, какой долей дохода владеет каждая группа населения. Затем по полученным накопленным итогам строится так называемая кривая Лоренца (графическое изображение уровня концентрации явления). Например, в Рязанской области около 500 домашних хозяйств представляют информацию о своих семейных бюджетах, где расписаны доходы и расходы. Такой ряд будет иметь примерно 15-18 интервалов. Интервальный ряд разбивается на квинтильные группы для построения кривой Лоренца.
Рис. 1. Кривая Лоренца
По закону Парето-Лоренца-Джини, чем больше доход, тем меньше людей его имеют. На графике кривой Лоренца по оси абсцисс откладываются квинтильные точки, по оси ординат – процентный уровень дохода. При равномерном распределении доходов каждая двадцатипроцентная группа населения имела бы пятую часть доходов общества. На графике это изображается диагональю квадрата и рассматривается как линия равномерного распределения, т.е. при равномерном распределении коэффициент Джини равен 0. При неравномерном распределении "линия концентрации" представляет собой вогнутую вниз кривую. Чем больше отклонение кривой Лоренца от диагонали квадрата, тем выше поляризация доходов общества. По квинтильным точкам можно провести параболу по методу наименьших квадратов. Если рассматривать кривую, то коэффициент Джини можно рассчитывается по формуле, Децильные коэффициенты дифференциации доходов рассчитываются как соотношения уровней верхнего и нижнего децилей вариационных рядов соответствующих показателей. Таким образом, децильный коэффициент показывает отношение минимального дохода 10 % самых богатых к максимальному доходу 10 % самых бедных. Коэффициент фондов показывает отношение средних значений признаков верхнего и нижнего интервалов. Коэффициент показывает, во сколько раз среднедушевой доход 10 % наиболее высокодоходного населения больше, чем у 10 % населения с наименьшими доходами. Среднее значение дохода населения в пределах одного квантиля находится как средневзвешенное. Для этого в качестве параметров берется среднее значение в каждом интервале дохода (интервальный ряд распределения с шагом h), а в качестве весов берутся количество или процент населения, имеющего доход, попадающий в соответствующий интервал. Показатели вариации: 1. Размах вариации является наиболее простым измерителем вариаций признака. Он представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности:
2. Средне линейное отклонение рассчитывается как средняя арифметическая взвешенная величина из отклонений вариантов признака от их средней.
где xi – i -й вариант признака, Этот показатель не очень удобен для использования, т.к. нужно брать разность по модулю. 3. Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины (s). Дисперсия вычисляется по формулам простой невзвешенной и взвешенной соответственно:
4. Среднеквадратическое отклонение представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней.
5. Для характеристики вариации признаков в совокупности можно применить так называемое квартильное отклонение. Этот показатель также можно применить вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений: q = (Q3 – Q1) / 2 где Q1, Q3 – соответственно первый и третий квартили. Наряду с абсолютными показателями существуют и относительные, которые получают из абсолютных путем деления на среднее значение 6. Коэффициент осцилляции:
7. Относительное линейное отклонение:
8. Коэффициент вариации:
Коэффициент вариации является одним из главных показателей в статистике. Его используют для определения степени риска. Если V > 30%, то риск отличен от 0; если же V < 30%, то риск примерно равен 0. 9. Относительное квартильное отклонение:
Момент распределения:
Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей асимметрии и эксцесса. 10. Для сравнительного анализа степени асимметрии нескольких распределений рассчитывают относительный показатель AS:
При нормальном распределении коэффициент асимметрии равен 0. Величина показателя асимметрии 11. Может быть также рассчитан показатель эксцесса (островершинности):
Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. В нормальном распределении
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 716; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.220.239 (0.008 с.) |

 .
. .
.
 .
. , где а - постоянное число.
, где а - постоянное число. .
.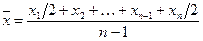

 – частота модального интервала;
– частота модального интервала; – частота домодального интервала;
– частота домодального интервала; – частота послемодального интервала.
– частота послемодального интервала. – это значение признака в той группе, в которой накопленная частность впервые превысит величину
– это значение признака в той группе, в которой накопленная частность впервые превысит величину  , где
, где  – номер квантилей. Аналогично определяется квантильный интервал для интервального ряда. Значение квантилей внутри интервального ряда:
– номер квантилей. Аналогично определяется квантильный интервал для интервального ряда. Значение квантилей внутри интервального ряда: .
.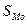 – частота квантильного интервала;
– частота квантильного интервала; – сумма накопленных частот предюдущего интервала;
– сумма накопленных частот предюдущего интервала; – сумма накопленных частот следующего за квантильным интервала.
– сумма накопленных частот следующего за квантильным интервала. значения, получаем разные квантили.
значения, получаем разные квантили.
 где
где 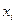 – доля населения в интервале,
– доля населения в интервале,  – доля доходов у этой доли населения, cumyi – кумулята, т.е. накопленный доход, где n – число интервалов.
– доля доходов у этой доли населения, cumyi – кумулята, т.е. накопленный доход, где n – число интервалов.

 ,
, – вес i -го варианта, n – объем совокупности.
– вес i -го варианта, n – объем совокупности. и
и  .
.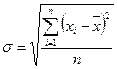 – невзвешенное,
– невзвешенное, – взвешенное.
– взвешенное. .
.









 .
.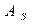 может быть положительной и отрицательной: если AS<0, то распределение левостороннее, если же AS>0, то распределение правостороннее.
может быть положительной и отрицательной: если AS<0, то распределение левостороннее, если же AS>0, то распределение правостороннее. .
. и показатель эксцесса равен 0. Если EX<0, то распределение туповершинное, т.е. вершина эмпирического распределения лежит ниже вершины кривой нормального распределения, при EX>0 соответственно наоборот распределение островершинное.
и показатель эксцесса равен 0. Если EX<0, то распределение туповершинное, т.е. вершина эмпирического распределения лежит ниже вершины кривой нормального распределения, при EX>0 соответственно наоборот распределение островершинное.


