
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические методы анализа динамики социально-экономических процессов и явлений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Динамическим или временным рядом называется ряд значений статистических показателей, расположенных в хронологической последовательности. Статистические показатели называются уровнями ряда и обозначаются Виды рядов динамики: § Интервальные. Уровень ряда характеризует состояние явления за интервал. Например, производство продукта за год. § Моментные. Уровень ряда характеризует состояние явления на определенную дату. Например, списочная численность работников предприятия. Уровни ряда должны быть сопоставимы, что означает одинаковый подход к единицам совокупности, одинаковую полноту охвата, единые цены (например, для цен пересчет производится при помощи индекса дефляции), равенство периодов, единую методологию расчета. Приведение ряда к сопоставимому виду называется смыканием. Показатели ряда динамики бывают базисными и цепными. Базисные показатели характеризуют окончательный результат всех изменений уровня от базисного периода до текущего, цепные характеризуют изменение уровней от периода к периоду. Существуют следующие показатели: 1. Абсолютный прирост: 2. Скорость роста: 3. Темп роста: 4. Цепной темп роста: 5. Темп прироста: 6. Цепной темп прироста: 7. Абсолютное значение 1% прироста (цепной показатель): 8. Для двух рядов может быть рассчитан коэффициент опережения:
Используются также средние характеристики ряда динамики: § для интервального ряда § для моментного ряда используется два способа. Первый – приближенный способ: При анализе динамических рядов надо выявить тренд и оценить вариацию (колеблемость) относительно тренда. Тренд характеризует тенденцию развития ряда. Выявление тренда называется выравнивание временного ряда. Различают следующие основные методы выравнивания: 1. Метод укрупненного интервала. Берется укрупненный интервал, например, вместо месяца квартал. Для интервального ряда новые уровни получаются методом простого суммирования, при этом колебания сглаживаются. Для моментального ряда находится среднее значение внутри укрупненного интервала. Достоинством такого метода является простота, а недостатком – более крупный уровень. 2. Метод скользящей средней. Укрупненный интервал сдвигается каждый раз на один уровень, и получаем многократное сглаживание. Например, первый квартал – январь, февраль, март; второй квартал – февраль, март, апрель и т.д. 3. Метод аналитического выравнивания (машинный метод). Находится аналитическая зависимость для тренда Основные виды зависимостей: 1. линейная 2. параболическая или полиномиальная 3. показательная или экспоненциальная 4. степенная 5. логистическая Тренд используется: § для качественного анализа: определяется рост, замедление, ускорение; § интерполяция – определение по тренду недостающего члена ряда; § экстраполяция – продолжение тренда в будущее, т.е. прогнозирование. Таким образом, зная тренд, можно сделать прогноз в предположении, что тенденция меняться не будет. Различают следующие основные типы колебаний статистических показателей: 1. Пилообразная или маятниковая колеблемость – переменное отклонение уровня ряда от тренда в разные стороны. Коэффициент автокорреляции равен -1. Например, урожайность. 2. Циклическая или долгопериодическая колеблемость. Коэффициент автокорреляции равен 1. Знак отклонения от тренда меняется редко, т.е. период большой. Например, процессы в экономике. 3. Случайно распределенная во времени колеблемость. Колебания накладываются друг на друга с различными характеристиками, например периодами, при этом их сложно предсказать. Коэффициент автокорреляции стремится к нулю. Например, при определении температуры нужно учитывать сезонные, суточные, погодные колебания, глобальное потепление. Колеблемость отличается от вариации: § причинами; § зависимостью уровней ряда друг от друга (автокорреляцией); § отклонением не от среднего значения, а от тренда. Показатели силы колебания аналогичны показателям вариации: 1. Амплитуда – отклонение уровней от тренда 2. Среднее линейное отклонение 3. Среднее квадратическое отклонение 4. Коэффициент колеблемости Особые колебания, возникающие под влиянием смен времен года, называют сезонными, они строго цикличны. Например, потребление электроэнергии, цены и потребление отдельных видов товаров, курс валют и т.д. При этом сезонные колебания характеризуются индексом сезонности
где Если существует тренд, то он сначала выявляется одним из известных методов, а затем индекс сезонности вычисляется как:
Индекс – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях, таким образом, это показатель сравнения двух состояний одного и того же явления, простого или сложного, состоящего из соизмеримых или несоизмеримых элементов. Различие условий может проявляться во времени (тогда говорят об индексах динамики), в пространстве (территориальные индексы), в выборе в качестве базы сравнения какого-либо условного уровня, например, планового показателя, уровня договорных обязательств и т. п. Соответственно вводят индекс выполнения обязательств или, если плановый уровень сравнивается с уровнем предыдущего периода, – индекс планового задания. Индексы включают в себя два вида данных: оцениваемые, которые называются отчетными и обозначаются "1", и базовые, которые используются в качестве базы сравнения и обозначаются "0". Сфера применения индексов: 1. сравнительная характеристика совокупностей (используются, как показатели динамики, выполнения плана, территориальные индексы и т.д.); 2. анализ факторов динамики, т.е. анализируются компонентные взаимосвязи статистических показателей (если имеется мультипликативная зависимость, то индекс показывает вклад каждой компоненты, например, в производстве интенсивным фактором работы является производительность труда, а экстенсивным – время работы); 3. анализ динамики средних величин. Классификация индексов: § По характеру изучаемых объектов различают индексы объемных показателей и индексы качественных показателей. § По степени охвата элементов совокупности различают индивидуальные индексы, которые сравнивают отдельные элементы совокупности и обозначаются i, и общие индексы, характеризующие изменение совокупности в целом и обозначающиеся I. Разновидностью общих индексов являются групповые индексы, которые характеризуют изменение части совокупности. § По форме представления и методам расчета общих индексов различают агрегатные индексы и средние из индивидуальных. § По виду данных, используемых в качестве базы, различают цепные индексы и базисные индексы. Основной формой общих индексов является агрегатный индекс, который имеет вид:
где Функции агрегатных индексов: 1. Синтетическая функция – в одном индексе непосредственно обобщаются несоизмеримые явления. Например, цены на хлеб в разное время. 2. Аналитическая функция следует из взаимосвязи индексов. Индекс можно рассматривать как составляющую некоторой системы индексов, он измеряет вклад одного из факторов в совокупные измерения. Если В зависимости от соотношения 1. Индекс Ласпереса (индекс цен): Веса у индекса берутся за базисный период. Первая форма записи – агрегатная. Вторая – средняя из индивидуальных. Формула представляет собой среднее арифметическое взвешенное по базисному периоду. 2. Индекс Паше:
Первая форма записи – агрегатная, вторая – средняя из индивидуальных. Формула представляет собой среднее гармоническое взвешенное по объему. 3. Индекс Фишера: 4. Индекс Эджворта Фишер предложил ряд тестов или свойств индексов: 1. идентичность: 2. соизмеримость: на величину индекса не должны влиять единицы измерения; 3. обратимость во времени: 4. циркулярность: 5. обратимость факторов 6. пропорциональность. Если все 7. определенность: 8. ассоциативность: Индекс Фишера удовлетворяет всем признакам, а индексы Ласпереса и Пааше не удовлетворяют пятому тесту, поэтому для составления системы индексов
Вторая система индексов в современной статистике используется для анализа себестоимости, но может использоваться и для анализа цен: 1. Индекс переменного состава отражает изменения средней цены:
2. На его базе индекса переменного состава может быть получен индекс постоянного или фиксированного состава (структура должна быть зафиксирована):
3. Индекс структуры (структура меняется, а цена фиксируется):
Индекс физического объема промышленной продукции используется для анализа и прогноза экономических процессов в стране и международных сравнений. Методика построения Iq основана на последовательном обобщении данных: 1. определяются структурные показатели промышленности 2. отбираются товары-представители, занимающие преобладающий удельный вес в каждой отрасли; 3. рассчитывается отраслевой индекс 4. определяется агрегатный индекс по промышленности: Для динамики потребления используется индекс потребительских цен (ИПЦ), характеризующий изменение среднего уровня цен на товары и услуги, приобретаемые типичным городским домашним хозяйством. Он используется для количественной оценки инфляции, для индексации заработной платы и трансфертов. ИПЦ является одним из показателей уровня жизни населения. Одним из источников данных являются данные наблюдения за ценами. Вторым источником информации для расчета ИПЦ являются данные бюджетной статистики. Около 500 домашних хозяйств учитывают свои доходы и расходы и представляют данные в комитет статистики. На основании этих двух источников по международной методике рассчитывается ИПЦ, который измеряет изменение стоимости из фиксированного набора товаров или потребительской корзины. ИПЦ также называют индексом стоимости жизни. Потребительская корзина составляют субъективно. Она состоит из трех частей: § продовольственные товары, порядка 60 наименований; § непродовольственные товары, порядка 40 наименований; § платные услуги, порядка 25 наименований. Методика расчета ИПЦ следующая: 1. Определяется средняя цена каждого товара потребительской корзины. Наблюдение ведется в разных точках. 2. Рассчитываются индивидуальные индексы по городу или области 3. Расчет базисного ИПЦ. Теоретически ИПЦ рассчитывается как индекс Ласпереса Расчетная формула следующая:
Используется 4-ое свойство Фишера и шестое свойство средней арифметической (т.е. веса заменяются их долями), форма представления как средняя из индивидуальных.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 942; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

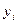 .
.






 .
.
 , где x0 – начальное значение, xк – конечное значение. Второй – вычисление средней хронологической
, где x0 – начальное значение, xк – конечное значение. Второй – вычисление средней хронологической  .
. . Эту зависимость можно рассматривать как регрессионную, где
. Эту зависимость можно рассматривать как регрессионную, где  – результативный признак,
– результативный признак,  – факторный признак.
– факторный признак.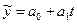 ;
;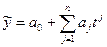 ;
; ;
; . Эту зависимость путем логарифмирования можно привести к линейной;
. Эту зависимость путем логарифмирования можно привести к линейной; .
. ;
;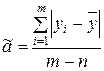 , где
, где  – число уровней ряда,
– число уровней ряда,  – число параметров тренда;
– число параметров тренда; ;
;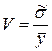 .
. , где
, где  - номер месяца, декады, недели. Совокупность индексов сезонности называют сезонной волной. Если тренд отсутствует, то индекс сезонности равен:
- номер месяца, декады, недели. Совокупность индексов сезонности называют сезонной волной. Если тренд отсутствует, то индекс сезонности равен:
 – средняя по годам в данном месяце,
– средняя по годам в данном месяце,  , где
, где  – количество лет,
– количество лет,  – общая средняя и по годам и по месяцам:
– общая средняя и по годам и по месяцам:  .
.

 – соизмеряемые показатели или индексируемые признаки,
– соизмеряемые показатели или индексируемые признаки,  – признаки веса.
– признаки веса.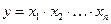 , то
, то 
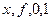 различают индексы:
различают индексы: , где
, где  .
. .
. .
.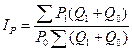 .
. ;
; ;
;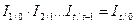 ;
; , если
, если  ;
; , то
, то 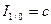 ;
; не должен обращаться в ноль или бесконечность, если некоторые
не должен обращаться в ноль или бесконечность, если некоторые  или
или  принимают нулевое значение;
принимают нулевое значение; .
.
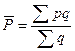 , где
, где  – структура совокупности.
– структура совокупности.
 .
.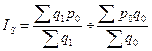
 – эта система является иллюстрацией принципа целостности, используется при анализе динамики себестоимости.
– эта система является иллюстрацией принципа целостности, используется при анализе динамики себестоимости. – веса или доля
– веса или доля  , где
, где  средние оптовые цены базисного периода;
средние оптовые цены базисного периода; . Индекс считается как среднее арифметическое взвешенное по каждой отрасли.
. Индекс считается как среднее арифметическое взвешенное по каждой отрасли. ,
, 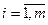 – номер торговой точки,
– номер торговой точки,  – номер товара.
– номер товара. , где
, где  – доля населения
– доля населения  района.
района.




