
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические методы анализа взаимосвязи социально-экономических явлений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Связи между общественными явлениями отражаются в статистических показателях, которые находятся между собой в определенных соотношениях. Причем одни из признаков выступают как факторные признаки или причины, другие как результативные признаки или следствия. Использование статистических методов анализа позволяет изучить, измерить и дать количественное выражение взаимосвязи между явлениями общественной жизни, установленными на основе качественного анализа. Виды взаимосвязей статистических показателей: 1. Факторные или корреляционные взаимосвязи. Они проявляются в согласованной вариации различных признаков у единиц одной и той же совокупности и изучаются с помощью аналитической группировки и корреляционно-регрессионного анализа. 2. Компонентные взаимосвязи – это такие взаимосвязи, когда изменения какого-то сложного явления целиком определяется изменением компонент, входящих в выражение, характеризующих сложное явление. В отличие от предыдущей связи, связи между показателем и компонентой жесткие. Изучаются эти показатели индексным методом. 3. Балансовые взаимосвязи служат для анализа балансовым методом пропорций в образовании ресурсов и их использования. Рассмотрим корреляционные или факторные показатели. Корреляционные взаимосвязи являются наряду с функциональными частным случаем статистической связи. Статистическая связь – это такая связь, что с изменением одной переменной вторая может в определенных пределах принимать любое значение, но ее статистические характеристики изменяются по определенному закону – разным значениям одной переменной соответствуют разные распределения другой. Частный случай корреляционной связи – функциональная связь. Функциональные взаимосвязи – это крайний случай, когда одному значению переменной соответствует четко заданное значение (одно или несколько). Когда одной переменной соответствует одно или несколько средних значений, то такая зависимость называется корреляционной. Корреляционная связь возникает различными путями: 1. Причинная зависимость вариации результативного признака от вариации факторного (напр., плодородие и урожайность). 2. Следствие общей причины (н апр., как зависит число пожаров и количество пожарных? Общая причина – это размер города. Чем больше город, тем больше пожаров и больше пожарных). 3. Оба признака являются и причиной и следствием (Напр., з/п и производительность труда). Формы корреляционной связи: § Прямая и обратная связь. Прямая связь – с увеличением факторного признака увеличивается и результативный. Обратная связь – с увеличением факторного признака результативный уменьшается. § Линейные связи и нелинейные. § Однофакторные связи и многофакторные. Если корреляционная связь такова, что преобладающая доля вариации результативного признака обусловлена вариацией факторных признаков, то зависимость между результативным и факторными признаками приблизительно можно считать функциональной и использовать эту зависимость для анализа и прогнозирования. Подобные зависимости или модели называются регрессионными или казуальными (амер. термин: казуальные модели, т.е. обусловленные) или корреляционно-регрессионными. Одним из методов выявления взаимосвязей является аналитическая группировка. Сначала статистическая совокупность группируется по факторному признаку, т.е. по нему строится распределение. После рассчитывается 3 дисперсии результативного признака, чтобы проследить вариацию признака по всей совокупности, а также количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. § Межгрупповая дисперсия:
где k номер группы (всего m групп), а fk число единиц в k -той группе. Межгрупповая дисперсия показывает рассеяние групповых средних относительно общих и характеризует вариацию результативного признака y за счет факторного признака x. § Внутригрупповая дисперсия:
§ Общая дисперсия: Все дисперсии связаны между собой правилом сложения дисперсий:
где
Для оценки тесноты связи между результативным (y) и факторным (х) признаками используется эмпирическое корреляционное отношение Рассмотрим схему построения казуальных моделей на примере построения прогнозной модели производительности труда. Первый этап. Постановка задачи – это четкое определение целей создания модели и объекта моделирования. Например, необходимо составить план по производительности труда на следующие 3 года на одном из предприятий. Необходимо определить от чего качественно зависит производительность труда, затем построить количественную модель, сделать прогноз по этим факторам и подставить прогнозные значения факторов в модель, а затем уже определить прогнозное значение производительности труда. Таким образом, следует определить от каких факторов зависит производительность труда, и при этом факторы должны быть управляемыми. Например, возьмем такие факторы: фондовооруженность, энерговооруженность, доля новой техники, коэффициент специализации. Второй этап. Сбор и систематизация статистической информации. Производительность труда называется результативным признаком – Встает вопрос о единицах совокупности, т.е. о точках выборки, которые могут быть разного рода. Если используются исследования в течение ряда лет, то точкой выборки станет год. Если рассматриваются эти показатели у всех предприятий за год, то точка выборки – завод. Если рассматривать показатели у ряда предприятий за ряд лет, то точка выборки – завод/год. Но лучше всего брать в качестве точки выборки год. Информация берется из документов и отчетов предприятия или предприятий. Причем исследуется максимальный перечень факторных признаков. Результат сбора информации оформляется в виде таблицы: m строк – точки выборки, n+1 столбцов – признаки. Первый столбец – результативный признак, а последующие факторные признаки. Точка выборки – год (квартал).
Третий этап. Статистическая оценка значимости факторов или корреляционный анализ позволяет включить в модель только те факторные признаки, которые существенно влияют на результативный. Для оценки степени влияния двух случайных величин
Коэффициент корреляции после преобразований примет вид:
где Результаты расчета коэффициентов парной корреляции оформляется в виде таблицы или корреляционной матрицы:
Матрица имеет единицы по диагонали и симметрична относительно главной диагонали. В нашем примере получена следующая таблица:
Факторные признаки отбираются в два шага. На первом шаге рассматриваются коэффициенты корреляции между результативными и факторными признаками. В модель включаются все факторные признаки, у которых │rxy│ больше некоторого наперед заданного значения. В нашем случае отбрасываем третий фактор. На втором шаге рассматриваются оставшиеся факторные признаки, т.е. рассматриваются коэффициенты парной корреляции между оставшимися факторными признаками. Если рассматриваемый показатель превышает некоторое наперед заданное значение, например 0,8, то один из факторных признаков исключается, а именно тот, у которого коэффициент парной корреляции с результативным признаком меньше. В обратном случае оба фактора включаются в модель. В нашем примере остается только фондовооруженность. Четвертый этап. Построение эмпирического уравнения регрессии предназначено для выявления характера взаимосвязей между результативным и факторным признаком. Графики строятся следующим образом. Ось абсцисс разбивается на интервалы точками xj. Строятся графики зависимостей Пятый этап. Построение однофакторных уравнений регрессии. Рассмотрим построение линейной регрессии.
Для нахождения коэффициентов регрессии
В результате получаем система нормальных уравнений:
Из этих уравнений получаем значение неизвестных коэффициентов регрессии:
Если зависимость нелинейная, то метод наименьших квадратов применять нельзя. Тогда следует привести зависимость к линейной при помощи некоторых приемов. Если зависимость показательная Шестой этап. Построение многофакторной регрессии. Ее построение начинается с выборы формы зависимости. Если среди эмпирических зависимостей преобладают линейные зависимости, то строится многофакторная линейная зависимость:
Если преобладает нелинейные зависимости, то и множественная регрессия будет нелинейной. Можно использовать в этом случае мультистепенную модель:
которую путем логарифмирования приводим к линейной:
Дифференцируя (XTX)*A = XTY где Решая систему относительно неизвестных коэффициентов регрессии, получаем: Четвертый, пятый и шестой этапы называют регрессионным анализом, который подразумевает построение различных уравнений регрессии, чтобы впоследствии выявить лучшую модель. Седьмой этап. Дисперсионный анализ или оценка точности и адекватности регрессионной модели. При оценке используются различные виды дисперсий: § общее рассеяние Dy; § рассеивание относительно уравнения регрессии D0; § рассеивание точек, лежащих на уравнении регрессии, относительно среднего значения; Общая дисперсия: Остаточная дисперсия (относительно уравнения регрессии): Дисперсия, обусловленная регрессией: В случае этих дисперсий также выполняется правило сложения дисперсий, но отдельно для числителя и отдельно для знаменателя. Для оценки точности используются следующие показатели: § Остаточная дисперсия, которая является относительной оценкой. Если у нас зависимость функциональная, то точка выборки будет лежать на уравнении регрессии и остаточная дисперсия будет равна нулю. Но в качестве абсолютного показателя остаточную дисперсию использовать нельзя, потому что она имеет размерность ед.2. § Коэффициент множественной корреляции, который показывает долю вариации результативного признака, обусловленного влиянием всех признаков, включенных в модель. Существует несколько формул для его расчета.
Если остаточная дисперсия равна нулю, то коэффициент равен единице, т.е. зависимость функциональная. Эта формула работает для достаточно хороших зависимостей. Воспользовавшись правилом сложения числителей дисперсий, получим:
Здесь надо вычислить матрицу, обратную матрице коэффициентов парной корреляции, и взять ее первый элемент § Средняя относительная ошибка:
§ Доверительный интервал позволяет оценить качество модели, для которой точки доверительного интервала вычисляются следующим образом:
где t – t-распределение; § Адекватность модели можно оценивать при помощи критерия Фишера:
Полученный критерий сравнивается с табличным значением, для вероятности
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.247 (0.008 с.) |

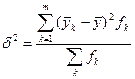
 – характеризует рассеяние внутри группы.
– характеризует рассеяние внутри группы.
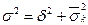
 – общая дисперсия, а
– общая дисперсия, а  – средняя из внутри групповых,
– средняя из внутри групповых,  – межгрупповая дисперсия:
– межгрупповая дисперсия: , а также коэффициент детерминации
, а также коэффициент детерминации  , который показывает, какая доля вариации
, который показывает, какая доля вариации  вызвана вариацией
вызвана вариацией  ,
,  . Если данный коэффициент равен нулю, то результативные и факторные признаки не связаны между собой, если же равен единице, то между ними существует функциональная зависимость.
. Если данный коэффициент равен нулю, то результативные и факторные признаки не связаны между собой, если же равен единице, то между ними существует функциональная зависимость. , факторные признаки – это признаки от которых зависит производительность труда
, факторные признаки – это признаки от которых зависит производительность труда  , где
, где  . Факторные признаки отбираются экспертным образом. При выборе факторного признака он должен быть количественно выражен; легко управляем; зависит от нас и влияет на производительность труда. Мы должны собрать информацию по этим признакам.
. Факторные признаки отбираются экспертным образом. При выборе факторного признака он должен быть количественно выражен; легко управляем; зависит от нас и влияет на производительность труда. Мы должны собрать информацию по этим признакам.
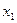 – фондовооруженность тыс.руб. на человека.
– фондовооруженность тыс.руб. на человека.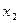 – энерговооруженность в киловаттах на человека.
– энерговооруженность в киловаттах на человека. – коэффициент специализации в процентах.
– коэффициент специализации в процентах.
 смешанный центральный момент второго порядка.
смешанный центральный момент второго порядка. 

 - объем выборки. Коэффициент парной корреляции меняется от -1(если функциональная зависимость обратная) до 1(если функциональная зависимость прямая). Если
- объем выборки. Коэффициент парной корреляции меняется от -1(если функциональная зависимость обратная) до 1(если функциональная зависимость прямая). Если 



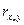


 . По ломаной можно судить, то ли зависимость линейная, то ли нелинейная. Если большинство зависимостей линейны, то и общая модель будет линейной.
. По ломаной можно судить, то ли зависимость линейная, то ли нелинейная. Если большинство зависимостей линейны, то и общая модель будет линейной. - уравнение линейной регрессии.
- уравнение линейной регрессии. используется метод наименьших квадратов.
используется метод наименьших квадратов. 
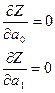


 , то можно использовать логарифмирование: log y = log a0 + a1*log x.
, то можно использовать логарифмирование: log y = log a0 + a1*log x.

 . Коэффициенты регрессии
. Коэффициенты регрессии  определяются при помощи метода наименьших квадратов:
определяются при помощи метода наименьших квадратов:
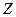 по
по  – матрица факторных признаков, полученных из таблицы исходных данных путем замены столбца результативных признаков на единицы. Матрица размерностью
– матрица факторных признаков, полученных из таблицы исходных данных путем замены столбца результативных признаков на единицы. Матрица размерностью  ,
,  – матрица-столбец результативного признака размерностью
– матрица-столбец результативного признака размерностью  – матрица-столбец коэффициентов регрессии размерностью
– матрица-столбец коэффициентов регрессии размерностью  .
.



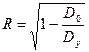
 ,
, 
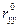 . Коэффициент множественной корреляции меняется от нуля до единицы, квадрат данного коэффициента называется коэффициентом детерминации и показывает долю изменчивости результативного признака за счет вариации всех факторных включенных в модель.
. Коэффициент множественной корреляции меняется от нуля до единицы, квадрат данного коэффициента называется коэффициентом детерминации и показывает долю изменчивости результативного признака за счет вариации всех факторных включенных в модель.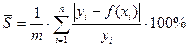 .
. – для однофакторной модели;
– для однофакторной модели; – для многофакторной модели,
– для многофакторной модели, – уровень риска; (
– уровень риска; ( ) – доверительная вероятность. Подкоренное выражение будет минимальным, когда
) – доверительная вероятность. Подкоренное выражение будет минимальным, когда  . Точность будет тем выше, чем меньше доверительный интервал. Следует отметить, что определение доверительного интервала эффективно в случае однофакторных моделей, т.к. для многофакторных моделей это ненаглядно.
. Точность будет тем выше, чем меньше доверительный интервал. Следует отметить, что определение доверительного интервала эффективно в случае однофакторных моделей, т.к. для многофакторных моделей это ненаглядно.

 и число степеней свободы
и число степеней свободы 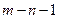 . Если вычисленное значение больше табличного, то модель адекватна. Таким образом, чем ближе зависимость к линейной, тем критерий Фишера больше. На практике желательно, чтобы вычисленное значение было больше табличного в четыре раза.
. Если вычисленное значение больше табличного, то модель адекватна. Таким образом, чем ближе зависимость к линейной, тем критерий Фишера больше. На практике желательно, чтобы вычисленное значение было больше табличного в четыре раза.


