
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка генеральной средней по выборочной средней. Устойчивость выборочных среднихСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть из генеральной совокупности (в результате независимых наблюдений над количественным признаком X)извлечена повторная выборка объема п со значениями признака x 1, х 2, …, xn. Не уменьшая общности рассуждений, будем считать эти значения признака различными. Пусть генеральная средняя хг неизвестна и требуется оценить ее по данным выборки. В качестве оценки генеральной средней принимают выборочную среднюю
Убедимся, что
Приняв во внимание, что каждая из величин Xl, X 2,..., Хn имеет то же распределение, что и генеральная совокупность (которую мы также рассматриваем как случайную величину), заключаем, что и числовые характеристики этих величин и генеральной совокупности одинаковы. В частности, математическое ожидание а каждой из величин равно математическому ожиданию признака X генеральной совокупности, т. е.
Заменив в формуле (*) математическое ожидание а на
Тем самым доказано, что выборочная средняя есть несмещенная оценка генеральной средней. Легко показать, что выборочная средняя является и состоятельной оценкой генеральной средней. Действительно, допуская, что случайные величины Xl, X 2,..., Хn имеют ограниченные дисперсии, мы вправе применить к этим величинам теорему Чебышева (частный случай), в силу которой при увеличении п среднее арифметическое рассматриваемых величин, т.е. Итак, при увеличении объема выборки п выборочная средняя стремится по вероятности к генеральной средней, а это и означает, что выборочная средняя есть состоятельная оценка генеральной средней. Из сказанного следует также, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом и состоит свойство устойчивости выборочных средних.
Заметим, что если дисперсии двух одинаково распределенных совокупностей равны между собой, то близость выборочных средних к генеральным не зависит от отношения объема выборки к объему генеральной совокупности. Она зависит от объема выборки: чем объем выборки больше, тем меньше выборочная средняя отличается от генеральной. Например, если из одной совокупности отобран 1% объектов, а из другой совокупности отобрано 4% объектов, причем объем первой выборки оказался большим, чем второй, то первая выборочная средняя будет меньше отличаться от соответствующей генеральной средней, чем вторая. Замечание. Мы предполагали выборку повторной. Однако полученные выводы применимы и для бесповторной выборки, еслиее объем значительно меньше объема генеральной совокупности. Это положение часто используется на практике.
Групповая и общая средние Допустим, что все значения количественного признака X совокупности, безразлично-генеральной или выборочной, разбиты на несколько групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти ее среднюю арифметическую. Групповой средней называют среднее арифметическое значений признака, принадлежащих группе. Теперь целесообразно ввести специальный термин для средней всей совокупности. Общей средней Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп, Опуская доказательство, приведем иллюстрирующий пример. Пример. Найти общую среднюю совокупности, состоящей изследующих двух групп:
Решение. Найдем групповые средние:
Найдем общую среднюю по групповым средним:
Замечание. Для упрощения расчета общей средней совокупности большого объема целесообразно разбить ее на несколько групп, найтигрупповые средние и по ним общую среднюю.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 719; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.89.0 (0.012 с.) |


 - несмещенная оценка, т. е. покажем, что математическое ожидание этой оценки равно
- несмещенная оценка, т. е. покажем, что математическое ожидание этой оценки равно 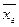 . Будем рассматривать
. Будем рассматривать 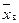 как случайную величину и x 1, х 2, …, xn как независимые, одинаково распределенные случайные величины Xl, X 2,.... Хn . Поскольку эти величины одинаково распределены, то они имеют одинаковые числовые характеристики, в частности одинаковое математическое ожидание, которое обозначим через а. Так как математическое ожидание среднего арифметического одинаково распределенных случайных величин равно математическому ожиданию каждой из величин (см. гл. VIII, § 9), то
как случайную величину и x 1, х 2, …, xn как независимые, одинаково распределенные случайные величины Xl, X 2,.... Хn . Поскольку эти величины одинаково распределены, то они имеют одинаковые числовые характеристики, в частности одинаковое математическое ожидание, которое обозначим через а. Так как математическое ожидание среднего арифметического одинаково распределенных случайных величин равно математическому ожиданию каждой из величин (см. гл. VIII, § 9), то (*)
(*)

 , стремится по вероятности к математическому ожиданию а каждой из величин, или, что то же, к генеральной средней
, стремится по вероятности к математическому ожиданию а каждой из величин, или, что то же, к генеральной средней  называют среднее арифметическое значений признака, принадлежащих всей совокупности.
называют среднее арифметическое значений признака, принадлежащих всей совокупности. = (10*1+15*6)/25=4;
= (10*1+15*6)/25=4;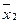 = (20*1+30*5)/50 = 3,4.
= (20*1+30*5)/50 = 3,4.


