
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики непрерывных случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Распространим определения числовых характеристик дискретных величин на величины непрерывные. Начнем с математического ожидания. Пусть непрерывная случайная величина X задана плотностью распределения f (x). Допустим, что все возможные значения X принадлежат отрезку [ а, b ]. Разобьем этот отрезок на п частичных отрезков длиной
Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл Математическим ожиданием непрерывной случайной величины- X, Возможные значения которой принадлежат отрезку [ a,b ], называют определенный интеграл M (X) = Если возможные значения принадлежат всей оси Ох, то M (X) = Предполагается, что несобственный интеграл сходится абсолютно, т. е. существует интеграл По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения X принадлежат отрезку[ a,b ], то D (X) = если возможные значения принадлежат всей оси х, то D (X) = Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством s(X) = Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин. Замечание 2. Легко получить для вычисления дисперсии более удобные формулы: D (X) = D (X) = Пример 1. Найти математическое ожидание и дисперсию случайной величины X, заданной функцией распределения
Решение. Найдем плотность распределения:
Найдем математическое ожидание по формуле (*): M (X) = Найдем дисперсию по формуле (**): D (X) = Пример 2. Найти математическое ожидание и дисперсию непрерывной случайной величины X, распределенной равномерно в интервале (а, b).
Решение. Найдем математическое ожидание X по формуле (*), учитывая, что плотность равномерного распределения f (x) = 1 / (b — а)(см. гл. XI, § 6): M (X) = Выполнив элементарные выкладки, получим M (X) = (a+b) / 2 Найдем дисперсию X по формуле (**): D (X) = Выполнив элементарные выкладки, получим D (X) = (b — a)2 / 12. Замечание 3. Математическое ожидание и дисперсия случайной величины R, распределенной равномерно в интервале (0, 1), т. е. если a = 0, b =1, как следует из примера 2, соответственно равны М (R) = 1/2, D(R)=l/12. Этот же результат мы получили в примере 1 по заданной функции распределения случайной величины R.
Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
Мы видим, что нормальное распределение определяется двумя параметрами: а иs. Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: а есть математическое ожидание, s—среднее квадратическое отклонение нормального распределения. а) По определению математического ожидания непрерывной случайной величины, M (X) = Введем новую переменную z = (x — а) / s. Отсюда x= s z+a, dx= s dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим M (X) = Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно a (интеграл Пуассона Итак, М (Х) = а, т. е. математическое ожидание нормального распределения равно параметру а. б) По определению дисперсии непрерывной случайной величины, учитывая, что М (Х) = а, имеем D (X) = Введем новую переменную z = (x — а) / s. Отсюда х — a = s z, dx = s0 dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим D (X) = Интегрируя по частям, положив u = z, dv= D (X) = s2. Следовательно, s(X) = Итак, среднее квадратическое отклонение нормального распределения равно параметру s. Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и s (s > 0). Нормированным называют нормальное распределение с параметрами а = 0 и s=1. Например, если X — нормальная величина с параметрами а и s, то U = (X — а) / s— нормированная нормальная величина, причем M (U) = 0, s(U) = 1.
Плотность нормированного распределения
Эта функция табулирована (см. приложение 1). Замечание 2. Функция F (х)общего нормального распределения (см. гл. XI, § 3)
а функция нормированного распределения
Функция Fo (x) табулирована. Легко проверить, что F (x) =F 0((x-a) / s). Замечание 3. Вероятность попадания нормированной нормальной величины X в интервал (0, х)можно найти, пользуясь функцией Лапласа P (0 <X<x) = Замечание 4. Учитывая, что
легко получить, что F 0(x) = 0, 5 + Действительно, F 0(x) =P (- Нормальная кривая
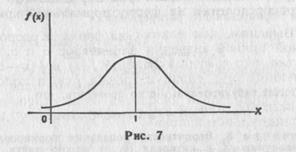
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию y= методами дифференциального исчисления. 1. Очевидно, функция определена на всей оси х.
2. При всех значениях х функция принимает положительные значения, т. е. нормальная кривая расположена над осью Ох. 3. Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю: 4.Исследуем функцию на экстремум. Найдем первую производную:
Легко видеть, что у' = 0 при х = а, у' > 0 при х < а, у' < 0 при х> а. Следовательно, при х = а функция имеет максимум, равный 5.Разность х — а содержится в аналитическом выражении функции в квадрате, т. е. график функции симметричен относительно прямой х= а. 6.Исследуем функцию на точки перегиба. Найдем вторую производную:
Легко видеть, что при х = а+s и х= а — s вторая производная равна нулю, а при переходе через эти точки онаменяет знак (в обеих этих точках значение функции равно 1 / ( На рис. 7 изображена нормальная кривая при а =1, s= 2
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.177.46 (0.012 с.) |

 ,
,  ,...,
,...,  и выберем в каждом из них произвольную точку xi (i = 1, 2,..., п). Нам надо определить математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений xi на вероятности попадания их в интервал
и выберем в каждом из них произвольную точку xi (i = 1, 2,..., п). Нам надо определить математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений xi на вероятности попадания их в интервал  ; (напомним, что произведение f (х)
; (напомним, что произведение f (х)  приближенно равно вероятности попадания X в интервал
приближенно равно вероятности попадания X в интервал 


 Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к —
Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к —  , а верхнего—к +
, а верхнего—к + 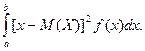
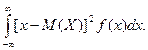
 .
.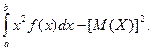 (**)
(**)




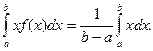

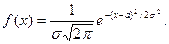


 ).
).

 , найдем
, найдем .
.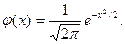

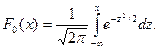
 Действительно (см.гл. XI, § 2),
Действительно (см.гл. XI, § 2),
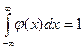 (см. гл. XI, §4,свойство 2), и, следовательно, в силу симметрии j(х)относительно нуля
(см. гл. XI, §4,свойство 2), и, следовательно, в силу симметрии j(х)относительно нуля , а значит, и Р (-
, а значит, и Р (-  < X < 0)=0,5,
< X < 0)=0,5, (x).
(x).
 , т. е. ось Ох служит горизонтальной асимптотой графика.
, т. е. ось Ох служит горизонтальной асимптотой графика.


 e)). Таким образом, точки графика (а — s, 1 / (
e)). Таким образом, точки графика (а — s, 1 / (


