
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние значения и моменты случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В зависимости от того, принадлежат ли возможные значения времени t и реализации X (t) дискретному множеству чисел или отрезку (а может быть, и всей действительной оси), различают четыре типа случайных процессов: 1) случайный процесс общего типа: t и X (t) могут принимать любые значения на отрезке или, быть может, на всей действительной оси; 2) дискретный случайный процесс: t непрерывно, а величины X (t) дискретны; 3) случайная последовательность общего типа: t дискретно, а X (t) может принимать любые значения на отрезке (или на всей) действительной оси; 4) дискретная случайная последовательность: t и X (t) оба дискретны. В любом случае, случайном или детерминированном, среднее значение есть сумма чисел, деленная на число величин, подлежащих усреднению. В случайной ситуации выборочное среднее величины X определяется как
Здесь черта над Х означает усреднение, а Можно также рассматривать понятие среднего, которое появляется при бесконечном числе испытаний. Такое гипотетическое среднее называется математическим ожиданием случайной величины. Рассмотрим дискретный случай. Случайная величина Х имеет n возможных значений
то есть среднее значение функции времени определяется ее интегрированием на некотором интервале времени, а затем делением полученной величины на продолжительность этого интервала. Для определения среднего значения непрерывной случайной величины усреднение по времени заменяют интегрированием по диапазону возможных значений, которые она может принимать, то есть вводится усреднение по ансамблю:
Здесь и далее угловые скобки означают операцию статистического усреднения, то есть усреднения по ансамблю. Отсюда вытекает следующее определение для математического ожидания дискретной случайной величины Х:
где n – число возможных значений случайной величины Х. Для непрерывной случайной величины
Таким образом, оператор вычисления математического ожидания для дискретной случайной величины представляет взвешенное суммирование, а для непрерывной случайной величины – интегрирование с весом. Качественно математическое ожидание представляет наиболее вероятное значение, а значения с каждой стороны от среднего становятся все менее и менее вероятными по мере того, как отклонение от среднего становится больше. Свойства математического ожидания: 1. Поскольку эти операторы линейны, математическое ожидание суммы случайных величин равно сумме математических ожиданий отдельных слагаемых. 2. Математическое ожидание константы рано ей самой. 3. Константу можно выносить за знак математического ожидания. Средние по времени значения важны при рассмотрении случайных функций времени, но говорить о среднем одиночного значения случайной величины не имеет смысла, поскольку оно определяется как мгновенное значение. Величины средних по ансамблю реализаций для любых степеней случайного процесса называются начальными моментами n -го порядка:
Центральные моменты n -го порядка определяются как
и представляют собой моменты для центрированного процесса
Самыми важными являются следующие моменты. 1. Начальный момент 1-го порядка, равный среднему значению. Также эта величина называется математическим ожиданием. Начальный момент 2-го порядка, равный среднему квадрату случайной величины:
Первый центральный момент всегда равен нулю
Второй центральный момент называется дисперсией
Дисперсия характеризует интенсивность флуктуаций случайного процесса. Корень квадратный из дисперсии σ(t) называется стандартным или среднеквадратическим отклонением. Существует еще одно определение дисперсии:
В качественном смысле дисперсия X представляет меру разброса X относительно среднего. Если среднее равно нулю, дисперсия тождественно равна второму начальному моменту. Можно показать, что
Так что дисперсия представляет разность между средним квадратом случайной величины и квадратом ее математического ожидания. Из свойств дисперсии отметим два: 1. Дисперсия неслучайной константы С равна нулю. 2. Неслучайную константу С выносят за знак дисперсии при возведении в квадрат. Третий центральный момент может служить критерием оценки для асимметрии закона распределения относительно оси, параллельной оси ординат и проходящей через среднее значение случайной величины. Часто пользуются понятием коэффициента асимметрии
Если для анализируемой кривой коэффициент асимметрии равен нулю, то по одному признаку эта кривая совпадает с нормальной. Однако равенство нулю коэффициента асимметрии еще не является достаточным условием нормальности распределения. Если кривая плотности вероятности имеет более пологий спад справа от среднего значения, говорят о положительной асимметрии Четвертый центральный момент. Иногда используют численную характеристику «сглаженности» кривой распределения около моды (максимального значения) – коэффициент эксцесса:
Этот коэффициент дает возможность сравнивать «характер вершины» данной кривой распределения с аналогичной особенностью нормального (гауссовского) распределения. Для нормального распределения случайного процесса К примеру, распределение молекул по скоростям описывается распределением Максвелла:
Здесь m – масса молекулы; k – постоянная Больцмана; Т – абсолютная температура. В этом случае коэффициент асимметрии равен 21. Коэффициенты γ и Из часто используемых видов функции распределения можно отметить применяемое в анализе распространения электромагнитных волн в хаотической неоднородной среде распределение Накагами или m –распределение. Если представить отдельную составляющую электромагнитного сигнала как
Здесь
При этом При При
поскольку В случае m >1 получаем обобщенное релеевское распределение:
где При Корреляционная функция Задание одномерной плотности распределения вероятности не дает возможности определить характер изменения случайного процесса во времени и не характеризует взаимосвязь случайного процесса в различные моменты времени. Зависимость между случайными процессами требует введения многомерных распределений. По аналогии с одномерным случаем вводят понятие двумерной плотности распределения вероятности
Для количественной характеристики зависимости случайных функций вводится нормированная корреляционная функция, которая называется коэффициентом корреляции:
Если коэффициент корреляции равен 1, это означает линейную зависимость случайных величин. Если они независимы, он равен нулю. В большинстве радиотехнических задач встречаются коэффициенты корреляции в виде монотонно убывающих или осциллирующих затухающих функций. Время затухания или время корреляции определяется как
Основные свойства корреляционной функции и коэффициента корреляции: 1. Равенство нулю для статистически независимых значений случайного процесса. Это следует из того, что
2. Симметричность относительно своих аргументов:
3. Ограниченность коэффициента корреляции:
Обозначим для простоты записи значения процесса через Если Если Легко определить, условия, при которых коэффициент корреляции двух процессов равен 0. Очевидно, такое равенство возможно в случае
Это возможно при условии Равенство коэффициента корреляции единице означает линейную зависимость случайных величин:
При нелинейной зависимости R отличается от единицы и в указанных пределах (-1,1) может принимать любые значения. Для коэффициента корреляции при
При
С увеличением временного сдвига коэффициент корреляции спадает от 1 до нуля. Коэффициент корреляции со временем спадает до нуля при бесконечном увеличении временного сдвига Значение коэффициента корреляции по уровню 0,5 определяет радиус (или интервал) корреляции в зависимости от разнесения (временного или пространственного). В случае одной реализации количественной мерой статистической зависимости последующего значения статистической величины от ее предыдущего значения является коэффициент автокорреляции. Можно рассматривать величины
при условии, что процесс стационарный Функция корреляции между значениями разных процессов называется взаимной корреляционной функцией.
Структурные функции. Понятие структурной функции часто применяется для анализа сред со случайными неоднородностями. Оно было введено акад. А.Н. Колмогоровым для описания поля скоростей турбулентных движений воздушных масс в атмосфере. По определению, структурная функция представляет величину
то есть средний квадрат разности значений случайной величины в двух точках. Пусть в точке 1 скорость является случайной величиной и равна Рассмотрим структурную функцию некоторого стационарного процесса. При этом несущественно, по времени или по пространству производится сдвиг.
Это выражение дает связь между корреляционной и структурной функциями и показывает, что для стационарного процесса возможно использование как той, так и другой. Корреляционная функция в максимуме равна квадрату дисперсии. Следовательно,
Мы показали, что Следовательно, для стационарного процесса получаем еще одну формулу, связывающую корреляционную и структурную функции:
Некоторые исследования, связанные с ограничением интервала усреднения, показывают: 1. Корреляционная функция дает б о льшую статистическую точность, если исследуемый объем состоит из множества мелких неоднородностей. 2. Если неоднородности крупные, б о льшую статистическую точность дают структурные функции.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 843; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.110.45 (0.008 с.) |

 . (33)
. (33) - выборочные значения, полученные при повторных испытаниях рассматриваемого случайного опыта.
- выборочные значения, полученные при повторных испытаниях рассматриваемого случайного опыта. . Если проведено m испытаний, где m – достаточно большое, то следует ожидать, что в
. Если проведено m испытаний, где m – достаточно большое, то следует ожидать, что в 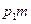 испытаниях появится значение
испытаниях появится значение 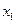 , в
, в  - значение
- значение  и т.д. Таким образом, выборочное среднее будет
и т.д. Таким образом, выборочное среднее будет , (34)
, (34) . (35)
. (35) , (36)
, (36) . (37)
. (37) . (38)
. (38) (39)
(39) . (40)
. (40) (41)
(41) . (42)
. (42) . (43)
. (43)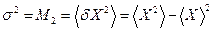 . (44)
. (44) . (45)
. (45)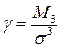 . (46)
. (46) . Если спад боле пологий слева от среднего значения, - коэффициент асимметрии отрицателен,
. Если спад боле пологий слева от среднего значения, - коэффициент асимметрии отрицателен,  , то есть плотность вероятности обладает отрицательной асимметрией.
, то есть плотность вероятности обладает отрицательной асимметрией. . (47)
. (47) =3. Отличие эксцесса от этой величины свидетельствует, что распределение не является нормальным. При
=3. Отличие эксцесса от этой величины свидетельствует, что распределение не является нормальным. При 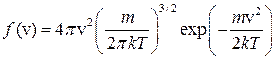 . (48)
. (48) , где R и
, где R и  - случайные амплитуда и фаза (изменение их по нормальному закону не требуется), то распределение огибающей этого сигнала, представляющей сумму большого числа компонент, описывается m -распределением:
- случайные амплитуда и фаза (изменение их по нормальному закону не требуется), то распределение огибающей этого сигнала, представляющей сумму большого числа компонент, описывается m -распределением: . (49)
. (49) . (50)
. (50) .
. получаем нормальное распределение как частный случай распределения Накагами.
получаем нормальное распределение как частный случай распределения Накагами.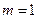 имеет место обычное распределение Релея:
имеет место обычное распределение Релея: , (51)
, (51)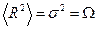 .
. , (52)
, (52) - функция Бесселя мнимого аргумента.
- функция Бесселя мнимого аргумента. , где n – целое и положительное, приходим к
, где n – целое и положительное, приходим к  -распределению.
-распределению. , описывающей связь двух значений X (t 1) и X (t 2) в произвольные моменты времени t 1 и t 2. С помощью двумерной плотности распределения вероятности можно определить корреляционную функцию, которая является вторым смешанным центральным моментом:
, описывающей связь двух значений X (t 1) и X (t 2) в произвольные моменты времени t 1 и t 2. С помощью двумерной плотности распределения вероятности можно определить корреляционную функцию, которая является вторым смешанным центральным моментом: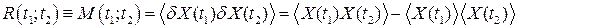 (53)
(53)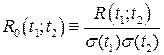 . (54)
. (54) . (55)
. (55) . (56)
. (56) . (57)
. (57) . (58)
. (58) и
и  . Если величины
. Если величины  , следовательно,
, следовательно,  .
. и
и  .
. ,
,  .
. . (59)
. (59) . Значит, в этом случае
. Значит, в этом случае  и
и  - независимые величины, так как при этом вероятность их совместного осуществления равна произведению вероятностей каждого из них. Итак, если
- независимые величины, так как при этом вероятность их совместного осуществления равна произведению вероятностей каждого из них. Итак, если 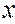 и
и  . (60)
. (60)
 . (61)
. (61)
 .
.  (62)
(62)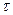 . Время корреляции
. Время корреляции  определяется по уровню
определяется по уровню 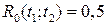 и дает ориентировочное представление о том, на каком временном интервале в среднем имеет место коррелированность случайного процесса. При меньшем значении радиуса корреляции считают, что корреляция между случайными величинами пренебрежимо мала.
и дает ориентировочное представление о том, на каком временном интервале в среднем имеет место коррелированность случайного процесса. При меньшем значении радиуса корреляции считают, что корреляция между случайными величинами пренебрежимо мала. и
и  как два различных, но связанных между собой процесса. Коэффициент корреляции определяет значение
как два различных, но связанных между собой процесса. Коэффициент корреляции определяет значение  , при котором процессы можно считать независимыми:
, при котором процессы можно считать независимыми: (63)
(63) , а не является функцией времени.
, а не является функцией времени. , (64)
, (64)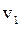 , а в точке 2 -
, а в точке 2 -  . Тогда структурная функция
. Тогда структурная функция  будет характеризовать связь между скоростями в двух точках.
будет характеризовать связь между скоростями в двух точках. . (65)
. (65) . То есть корреляционная функция в нуле принимает максимальное значение, структурная – минимальное. На
. То есть корреляционная функция в нуле принимает максимальное значение, структурная – минимальное. На  корреляционная функция равна нулю, структурная
корреляционная функция равна нулю, структурная 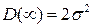 . Поскольку
. Поскольку  , получаем:
, получаем: . (66)
. (66) .
. . (67)
. (67)


