
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность при n независимых испытанияхСодержание книги
Поиск на нашем сайте
Лекция 2. Не будет преувеличением утверждать, что для каждого исследователя, имеющего дело с прецизионными измерениями, связанными с неизбежными погрешностями и фоном помех, владение методами теории вероятностей и понимание случайных процессов следует рассматривать как неотъемлемую часть общетеоретической грамотности, поскольку точность и достоверность проводимых измерений должны быть грамотно оценены. Каждому в практической деятельности приходится сталкиваться, к примеру, с выполнением многократных измерений. При этом результаты будут определяться точностью используемых для измерений устройств. Если говорить о случайных процессах, здесь мы часто сталкиваемся с понятием флуктуаций. Под флуктуациями понимаются случайные отклонения макроскопических величин от их средних (в частности, термодинамически равновесных) значений. Существование таких отклонений связано с наличием у всякой макроскопической системы огромного числа степеней свободы, если не макроскопических (как, например, у распределенных систем), то уж, во всяком случае, м икроскопических, обусловленных, в конечном счете, атомизмом вещества и электричества. Эта общая основа флуктуационных явлений допускает самые разнообразные механизмы их возникновения. Причинами возникновения флуктуаций могут стать: 1 - тепловое движение микрочастиц (электронов, ионов и т.д.); 2 - тепловые изменения самых разнообразных макровеличин (плотность, давление, температура, возникновение броуновского движения, тепловые шумы в радиотехнике и радиофизике, тепловое излучение тел и др.); 3 - случайные вариации числа частиц в электронных потоках при термо- и фотоэмиссии (так называемый дробовой эффект, непосредственно обусловленный дискретностью микроскопических носителей заряда); 4 - неравномерность процессов генерации и рекомбинации носителей тока в полупроводниковых приборах; случайные локальные вариации эмиссионных свойств поверхности катодов (эффект мерцания). К флуктуационным явлениям, которые связаны с наличием множества макроскопических степеней свободы, относятся такие процессы, как турбулентность среды – земной тропосферы и ионосферы, солнечной короны, межпланетной и межзвездной среды. Отсюда вытекает, что изучение физических явлений, существенных для связи и передачи информации, – генерации электромагнитных сигналов, излучения и распространения электромагнитных волн, приема радиосигналов, - определяется областью исследований статистической радиофизики. Сюда относятся в первую очередь флуктуации в автоколебательных системах и связанные с ними вопросы о немонохроматичности автоколебаний, о стабильности частоты и точности ее измерения (а значит, и точности измерения времени). При распространении волн интерес вызывают случайные тепловые и турбулентные неоднородности среды, поскольку они вызывают рассеяние радиоволн, случайные пульсации рефракции, случайные колебания интенсивности, фазы и других параметров волны и пучка в месте приема. Сюда же относится и вопрос о влиянии случайных неоднородностей в фидерах, волноводах или световодах, когда излучение распространяется не свободно, а по направляющим линиям. Одной из важных статистических задач, относящихся к излучению радиоволн, является вопрос о роли случайных неоднородностей в сложных антенных системах. Наконец, при приеме любого вида радиосигналов чрезвычайно существенны шумы в приемных и измерительных устройствах, трансформация внешних и внутренних шумов при разного рода преобразованиях сигнала в аппаратуре, вопрос о помехоустойчивости приемных систем и т.д. Вводные положения Вспомним кратко исходные положения теории вероятностей, необходимых для использования указанных применений. Если число возможных событий обозначить через n, а число благоприятных исходов – через m, вероятность событий определяется отношением:
Пример: Для иллюстрации этого определения обычно рассматривают пример с подбрасыванием монеты. Вероятность выпадения герба при одном подбрасывании равна ½. Какова вероятность выпадения герба при двух подбрасываниях? На самом деле при двух подбрасываниях герб может: а - выпасть в первом случае, но не выпадет во втором; b - во втором случае, но не в первом; c - и в первом, и во втором случаях; d - не выпадет ни в первом, ни во втором случаях. При этом из общего числа четырех возможных вариантов три являются благоприятными. Таким образом, вероятность выпадения герба будет равна ¾. Вероятность, равная единице, характеризует достоверное событие. Однако равенство вероятности нулю не означает, что событие невозможно. Скажем, для исследований нужен образец длины Крайне важно отметить при этом, что случайность события вовсе не означает его беспричинности. Случайные события подчинены своим статистическим законам. И именно изучение этих законов позволяет оптимизировать их применение на практике. Пусть есть цепь событий А; В; С … Если одновременно произошли события А и В, такое одновременное их осуществление называют произведением событий: АВ = С. (2) Запись А + В = С (3) означает осуществление одного из событий А или В. Если имеем две области событий, А и В, графически осуществимость этих событий будет характеризоваться областью пересечения областей А и В. События могут быть зависимыми и независимыми, совместными и несовместными. Несовместность событий – частный случай зависимости. Пусть события А и В независимы. Тогда вероятность одновременного осуществления событий
Пусть имеется система n событий. Выделим из них m событий. Число благоприятных случаев обозначим через l. Вероятность события l, очевидно, будет равна
При этом Обобщая, запишем:
Здесь Эта формула является исходной и может быть обобщена на случай совместного осуществления n событий. В качестве примера обычно рассматривают пример с покупкой k из m выпущенных билетов, из которых число выигрышных n. Требуется оценить вероятность выигрыша хотя бы по одному из них. Анализ показывает, что вероятность выигрыша будет равна
Для расчета факториалов при больших n можно использовать формулу Стирлинга:
Таким образом, если имеется система событий
Следовательно, полная вероятность события
Рассмотрим вопрос о вероятности суммы двух событий. Сумма двух событий – это осуществление любого из них. Если события несовместимы, то вероятность их суммы равна сумме вероятностей каждого из них:
В качестве примера обычно рассматривают бросание кубика. Вероятность выпадения единицы, двойки и т.д. равна 1/6. События эти несовместимы. Следовательно, вероятность выпадения единицы или двойки равна Но события могут быть и совместимыми. Очевидно, что вероятность события А складывается из вероятности совместного осуществления событий А и В и вероятности совместного осуществления событий А и не В (обозначим через
Записывая аналогично вероятность события В, получим выражение вероятности для их суммы:
Из нее можно получить выражение для суммы несовместных событий (12), поскольку в этом случае Формула Байеса Формула Байеса связана с очень важной в настоящее время проблемой выделения сигналов на фоне шумов и касается так называемой «переоценки гипотез». Пусть имеется ряд возможных исходов какой-либо операции. Обозначим их как события К примеру, это могут быть записи интенсивности сигнала на фоне шумов. Наличие сигнала обозначим через событие К. Пусть предварительно известны вероятности Как следует из формулы условной вероятности (6),
Предстоит определить Очевидно,
Здесь Формула Байеса является отражением причинно-следственной связи в случайных явлениях. Она показывает, как надо изменить апостериорные вероятности Пример: Имеется три совершенно одинаковых ящика. Пусть в одном находятся два белых шара, во втором - один белый и один чёрный, в третьем – два черных. Предположим, мы вытащили шар из одного из ящиков, и он оказался белым. Рассчитать вероятность того, что в ящике остался тоже белый шар. Очевидно, априорная вероятность правильного выбора ящика 1 – два белых шара:
2 – один белый и один черный шар:
Очевидно, что для третьего ящика искомая вероятность равна нулю:
Обобщая формулу полной вероятности и теорему Байеса (15) на случай непрерывно изменяющихся случайных величин – случайного процесса, - найдём, что условная плотность вероятности
где Корреляционная функция Задание одномерной плотности распределения вероятности не дает возможности определить характер изменения случайного процесса во времени и не характеризует взаимосвязь случайного процесса в различные моменты времени. Зависимость между случайными процессами требует введения многомерных распределений. По аналогии с одномерным случаем вводят понятие двумерной плотности распределения вероятности
Для количественной характеристики зависимости случайных функций вводится нормированная корреляционная функция, которая называется коэффициентом корреляции:
Если коэффициент корреляции равен 1, это означает линейную зависимость случайных величин. Если они независимы, он равен нулю. В большинстве радиотехнических задач встречаются коэффициенты корреляции в виде монотонно убывающих или осциллирующих затухающих функций. Время затухания или время корреляции определяется как
Основные свойства корреляционной функции и коэффициента корреляции: 1. Равенство нулю для статистически независимых значений случайного процесса. Это следует из того, что
2. Симметричность относительно своих аргументов:
3. Ограниченность коэффициента корреляции:
Обозначим для простоты записи значения процесса через Если Если Легко определить, условия, при которых коэффициент корреляции двух процессов равен 0. Очевидно, такое равенство возможно в случае
Это возможно при условии Равенство коэффициента корреляции единице означает линейную зависимость случайных величин:
При нелинейной зависимости R отличается от единицы и в указанных пределах (-1,1) может принимать любые значения. Для коэффициента корреляции при
При
С увеличением временного сдвига коэффициент корреляции спадает от 1 до нуля. Коэффициент корреляции со временем спадает до нуля при бесконечном увеличении временного сдвига Значение коэффициента корреляции по уровню 0,5 определяет радиус (или интервал) корреляции в зависимости от разнесения (временного или пространственного). В случае одной реализации количественной мерой статистической зависимости последующего значения статистической величины от ее предыдущего значения является коэффициент автокорреляции. Можно рассматривать величины
при условии, что процесс стационарный Функция корреляции между значениями разных процессов называется взаимной корреляционной функцией.
Структурные функции. Понятие структурной функции часто применяется для анализа сред со случайными неоднородностями. Оно было введено акад. А.Н. Колмогоровым для описания поля скоростей турбулентных движений воздушных масс в атмосфере. По определению, структурная функция представляет величину
то есть средний квадрат разности значений случайной величины в двух точках. Пусть в точке 1 скорость является случайной величиной и равна Рассмотрим структурную функцию некоторого стационарного процесса. При этом несущественно, по времени или по пространству производится сдвиг.
Это выражение дает связь между корреляционной и структурной функциями и показывает, что для стационарного процесса возможно использование как той, так и другой. Корреляционная функция в максимуме равна квадрату дисперсии. Следовательно,
Мы показали, что Следовательно, для стационарного процесса получаем еще одну формулу, связывающую корреляционную и структурную функции:
Некоторые исследования, связанные с ограничением интервала усреднения, показывают: 1. Корреляционная функция дает б о льшую статистическую точность, если исследуемый объем состоит из множества мелких неоднородностей. 2. Если неоднородности крупные, б о льшую статистическую точность дают структурные функции. Флуктуации уровня и фазы Амплитудно-фазовые флуктуации в случайно-неоднородной среде принято описывать величиной Следует отметить, что Выделим в выражении (152) действительную и мнимую части:
Отсюда на основании (143) находим:
Эти формулы выражают флуктуации фазы и уровня в среде со случайными неоднородностями. Они справедливы приближенно при упомянутом выше условии:
Учитывая статистический характер флуктуаций показателя преломления
Это неравенство эквивалентно соотношениям:
Первое из этих соотношений справедливо, если рассеяние мало на расстояниях порядка длины волны, т.е. уровень сигнала на этих расстояниях сохраняется почти постоянным. Второе неравенство (156) требует малости изменения угла отклонения луча от первоначального направления. Поскольку
Аналогично,
Следовательно,
то есть все поперечные компоненты градиента фазы малы по сравнению с продольной составляющей. Иными словами, угол отклонения луча от первоначального направления мал. Первое из условий (156) в реальных случаях земной атмосферы выполняется во всех случаях, когда флуктуации показателя преломления малы. Второе условие осуществимо в тех случаях, когда размеры неоднородностей велики по сравнению с длиной волны, поскольку мелкомасштабные неоднородности создают изотропное рассеяние, а крупные переизлучают в пределах узкого конуса в направлении распространения. Угол раствора конуса пропорционален 1/ ka. При этом отклонение луча от первоначального направления будет малым, если амплитуда рассеянной волны значительно меньше амплитуды падающей волны. Для волн оптического диапазона тропосферные неоднородности представляют неоднородности больших размеров. Это означает, что полученные выше результаты служат важной теоретической основой исследования вариаций поля оптической волны, распространяющейся в реальных условиях вблизи земной поверхности. Учитывая малость углов отклонения от направления волны, падающей на среду с неоднородностями, можно считать, что в формулах (154)
при Используя выражение для q (136), запишем:
Лекция 18 октября 2016 г.
Таким образом, получаем выражения для флуктуаций уровня и фазы в малоугловом приближении:
Эти формулы позволяют найти основные статистические параметры, характеризующие вариации уровня и фазы волны, распространяющейся в среде со случайными неоднородностями. Пусть прием ведется в точке
(159)
Здесь
- коэффициент корреляции случайных изменений Как свидетельствуют соотношения (159), средние квадраты флуктуаций фазы и уровня определяются видом корреляционной функции флуктуаций показателя преломления. Последняя в свою очередь зависит от конкретных свойств среды распространения. При практическом использовании результатов, полученных методом плавных возмущений, отметим, что с точки зрения сделанных при его обосновании допущений он применим лишь для малых флуктуаций уровня и фазы. Однако рядом исследователей установлено, что указанные условия следует рассматривать как достаточные, но не необходимые. Было показано, что в части, относящейся к флуктуациям фазы, метод справедлив практически для любой наблюдаемой в эксперименте величины фазовых флуктуаций. Что же касается флуктуаций уровня, то метод дает заметные ошибки при
Сильная турбулентность В настоящее время интенсивно развивается теория распространения электромагнитных волн в средах с сильно развитой турбулентностью в применении к пучкам и длинным трассам. Выяснилось, что экспериментальные результаты, полученные на сравнительно длинных трассах, не находят теоретического объяснения в рамках метода плавных возмущений. Было показано, что приближение метода плавных возмущений эквивалентно модели распространения волн в виде случайных фазовых экранов без учета многократного рассеяния на турбулентных неоднородностях. Вызванное этим обстоятельством развитие теории привело к привлечению новых методов (диаграммной техники, теории переноса излучения и других. Среди них значительное внимание было уделено методу параболического уравнения (или марковскому приближению).
Ма́рковский проце́сс — случайный процесс, эволюция которого после любого заданного значения временно́го параметра tt {\displaystyle t} Связь между нормальными и марковскими процессами состоит в том, что они частично пересекаются.
Ограничимся краткими сведениями об основных результатах анализа распространения пучков на длинных трассах. В основу вычислений положим волновое уравнение для среды с переменным показателем преломления
Здесь Представим электрическое поле пучка волн, распространяющихся вдоль оси х, в виде:
Подставляя это выражение в волновое уравнение (169), пренебрежем членом Воспользуемся приближенным равенством Тогда
Это уравнение носит название параболического приближения и описывает распространение пучков в условиях малой угловой расходимости (поскольку мы пренебрегли величиной
В эти выражения входят значения так называемых внутреннего и внешнего размеров неоднородностей и структурной характеристики флуктуаций, характеризующей интенсивность турбулентных возмущений показателя преломления на трассе. Первое из них налагает требование узконаправленности диаграммы рассеяния неоднородностей в направлении распространения. Второе означает пренебрежимо малый уровень рассеяния мощности поля на расстояниях порядка длины волны. Для типичных значений параметров трасс и турбулентности эти условия выполняются в оптическом диапазоне для трасс длиной в сотни километров. От полученного уравнения можно перейти к уравнениям для моментов случайной величины Е разных порядков. Метод такого перехода основан на предположении о дельта-коррелированности флуктуаций показателя преломления Выразим аналитически дельта-коррелированность флуктуаций величины n:
Здесь
Функциона́л — это отображение, заданное на произвольном множестве и имеющее числовую область значений: обычно множество вещественных чисел R {\displaystyle \mathbb {R} } Справка по вариационной производной: Функционал записывается в виде:
Это прямой аналог дифференциала функции конечномерного аргумента ( Производная Фреше, – аналог одномерного градиента, - называется вариационной производной:
Здесь выражение в круглых скобках – скалярное произведение;
Сумма представляет собой полный дифференциал. Если представить
можно записать
Далее воспользуемся соотношением, выражающим корреляцию между нормально распределенной случайной величиной
где через Принимая эти соотношения, мы тем самым приписываем случайной величине Возьмем теперь в качестве функционала
Это уравнение разрешимо относительно первого момента случайного поля
где
Принимая, что
находим интеграл от
Для случая плоской волны, то есть при
Подобная процедура может быть применена и для вычисления других моментов поля. Так, для вывода уравнения, которому удовлетворяет второй момент поля, нужно уравнение (171) умножить на Запишем второй момент флуктуаций поля
Решая это уравнение методом преобразования Фурье, находим: | ||
|
| Поделиться: |

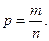 (1)
(1) Нельзя утверждать, что при изготовлении этот размер будет соблюдаться точно, - возможны отклонения от
Нельзя утверждать, что при изготовлении этот размер будет соблюдаться точно, - возможны отклонения от 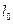 на величину
на величину  . Оценим вероятность того, что длина образца окажется равной
. Оценим вероятность того, что длина образца окажется равной  , то есть равно
, то есть равно  . Следовательно, искомая вероятность равна нулю. Однако равенство длины образца величине
. Следовательно, искомая вероятность равна нулю. Однако равенство длины образца величине  . (4)
. (4)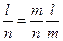 . (5)
. (5) - вероятность события m.
- вероятность события m.  - вероятность события m при условии, что событие m произошло.
- вероятность события m при условии, что событие m произошло. . (6)
. (6) – условная вероятность события В (при условии, что событие А осуществилось).
– условная вероятность события В (при условии, что событие А осуществилось).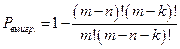 . (7)
. (7) . (8)
. (8) и от них зависит вероятность события
и от них зависит вероятность события 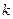 , совершающегося при осуществлении одного из событий
, совершающегося при осуществлении одного из событий  , то для каждого
, то для каждого  . (9)
. (9)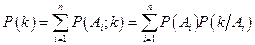 . (10)
. (10) . (11)
. (11)
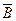 ):
): . (12)
. (12) (13)
(13)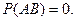 Из этого выражения следует также, что в общем случае вероятность суммы двух событий меньше или равна сумме вероятностей каждого из них.
Из этого выражения следует также, что в общем случае вероятность суммы двух событий меньше или равна сумме вероятностей каждого из них. .
. реализаций
реализаций  события К при осуществлении события
события К при осуществлении события  (14)
(14)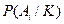 .
.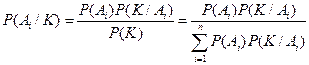 . (15)
. (15)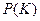 - полная вероятность события К. Понятие полной вероятности применяется в тех случаях, когда имеется неопределенность относительно причин, вызывающих следствие K. Для снятия этой неопределенностивыдвигается ряд гипотез
- полная вероятность события К. Понятие полной вероятности применяется в тех случаях, когда имеется неопределенность относительно причин, вызывающих следствие K. Для снятия этой неопределенностивыдвигается ряд гипотез 
 . Вероятность того, что вытащим белый шар, будет различна для разных ящиков. Для того, в котором находятся два белых шара, она равна
. Вероятность того, что вытащим белый шар, будет различна для разных ящиков. Для того, в котором находятся два белых шара, она равна  . Для ящика, в котором один из шаров – черный, эта вероятность равна
. Для ящика, в котором один из шаров – черный, эта вероятность равна  . Для третьего ящика она равна нулю. Эти вероятности известны нам до опыта. Найдем апостериорные вероятности того, что мы взяли шар из ящика, где было:
. Для третьего ящика она равна нулю. Эти вероятности известны нам до опыта. Найдем апостериорные вероятности того, что мы взяли шар из ящика, где было: ;
; .
.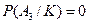 .
. случайной величины
случайной величины 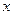 при условии, что А имело место, дается формулой:
при условии, что А имело место, дается формулой: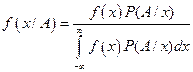 , (16)
, (16)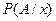 - вероятность события А при условии, что случайная величина приняла значение х;
- вероятность события А при условии, что случайная величина приняла значение х; 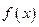 в дано случае - плотность вероятности случайной величины х до опыта (см. следующую лекцию).
в дано случае - плотность вероятности случайной величины х до опыта (см. следующую лекцию). , описывающей связь двух значений X (t 1) и X (t 2) в произвольные моменты времени t 1 и t 2. С помощью двумерной плотности распределения вероятности можно определить корреляционную функцию, которая является вторым смешанным центральным моментом:
, описывающей связь двух значений X (t 1) и X (t 2) в произвольные моменты времени t 1 и t 2. С помощью двумерной плотности распределения вероятности можно определить корреляционную функцию, которая является вторым смешанным центральным моментом: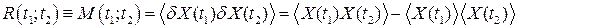 (53)
(53)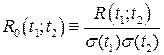 . (54)
. (54) . (55)
. (55) . (56)
. (56) . (57)
. (57) . (58)
. (58) и
и  . Если величины
. Если величины  , следовательно,
, следовательно,  .
. и
и  .
. ,
,  .
. . (59)
. (59) . Значит, в этом случае
. Значит, в этом случае  и
и  - независимые величины, так как при этом вероятность их совместного осуществления равна произведению вероятностей каждого из них. Итак, если
- независимые величины, так как при этом вероятность их совместного осуществления равна произведению вероятностей каждого из них. Итак, если 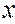 и
и  . (60)
. (60)
 . (61)
. (61)
 .
.  (62)
(62)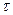 . Время корреляции
. Время корреляции  определяется по уровню
определяется по уровню 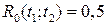 и дает ориентировочное представление о том, на каком временном интервале в среднем имеет место коррелированность случайного процесса. При меньшем значении радиуса корреляции считают, что корреляция между случайными величинами пренебрежимо мала.
и дает ориентировочное представление о том, на каком временном интервале в среднем имеет место коррелированность случайного процесса. При меньшем значении радиуса корреляции считают, что корреляция между случайными величинами пренебрежимо мала. и
и  как два различных, но связанных между собой процесса. Коэффициент корреляции определяет значение
как два различных, но связанных между собой процесса. Коэффициент корреляции определяет значение  , при котором процессы можно считать независимыми:
, при котором процессы можно считать независимыми: (63)
(63) , а не является функцией времени.
, а не является функцией времени. , (64)
, (64)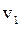 , а в точке 2 -
, а в точке 2 -  . Тогда структурная функция
. Тогда структурная функция  будет характеризовать связь между скоростями в двух точках.
будет характеризовать связь между скоростями в двух точках. . (65)
. (65) . То есть корреляционная функция в нуле принимает максимальное значение, структурная – минимальное. На
. То есть корреляционная функция в нуле принимает максимальное значение, структурная – минимальное. На  корреляционная функция равна нулю, структурная
корреляционная функция равна нулю, структурная 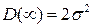 . Поскольку
. Поскольку  , получаем:
, получаем: . (66)
. (66) .
. . (67)
. (67) , характеризующей отклонение фазы световых колебаний от фазы плоской однородной волны, и величиной
, характеризующей отклонение фазы световых колебаний от фазы плоской однородной волны, и величиной  , определяющей флуктуации уровня сигнала.
, определяющей флуктуации уровня сигнала.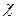 отличается от флуктуаций амплитуды
отличается от флуктуаций амплитуды  , где A – средняя амплитуда. Величина χ отличается и от флуктуаций логарифма амплитуды
, где A – средняя амплитуда. Величина χ отличается и от флуктуаций логарифма амплитуды  . Однако при
. Однако при  можно приближенно считать
можно приближенно считать  .
. . (153)
. (153)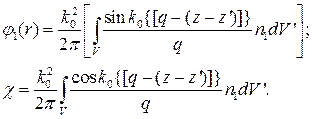 (154)
(154)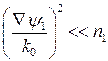 .
. , запишем это условие в виде:
, запишем это условие в виде: (155)
(155) . (156)
. (156) , получаем:
, получаем:



 .
.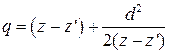 ,
,
 (157)
(157) (158)
(158) . Найдем средние квадраты случайных величин
. Найдем средние квадраты случайных величин  :
:

 Таким образом, метод плавных возмущений позволяет осуществлять оценки в весьма широком диапазоне амплитудно-фазовых флуктуаций.
Таким образом, метод плавных возмущений позволяет осуществлять оценки в весьма широком диапазоне амплитудно-фазовых флуктуаций. не зависит от эволюции, предшествовавшей tt {\displaystyle t}, при условии, что значение процесса в этот момент фиксировано («будущее» процесса не зависит от «прошлого» при известном «настоящем»; другая трактовка (Вентцель): «будущее» процесса зависит от «прошлого» лишь через «настоящее»).
не зависит от эволюции, предшествовавшей tt {\displaystyle t}, при условии, что значение процесса в этот момент фиксировано («будущее» процесса не зависит от «прошлого» при известном «настоящем»; другая трактовка (Вентцель): «будущее» процесса зависит от «прошлого» лишь через «настоящее»). , случайно меняющимся в пространстве и времени:
, случайно меняющимся в пространстве и времени: . (169)
. (169)
 . (170)
. (170) .
. .
. . (171)
. (171) и другими членами). Условия применимости этого приближения известны и могут быть записаны в виде неравенств:
и другими членами). Условия применимости этого приближения известны и могут быть записаны в виде неравенств: (172)
(172) (173)
(173) – пространственный спектр флуктуаций показателя преломления,
– пространственный спектр флуктуаций показателя преломления,  - волновой вектор,
- волновой вектор,  - вектор в плоскости
- вектор в плоскости 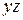 .
.
 ).
).
 - градиент функции y;
- градиент функции y; - оператор частной производной по –ой координате.
- оператор частной производной по –ой координате. .
. - вариационная производная Ф по
- вариационная производная Ф по  .
. в такой форме:
в такой форме: , (174)
, (174) обозначена вариационная производная.
обозначена вариационная производная. . Усредним уравнение (171) и подставим вместо
. Усредним уравнение (171) и подставим вместо  выражение, полученное при помощи соотношения (174). Используя дельта-коррелированность флуктуаций показателя преломления, после вычислений найдем:
выражение, полученное при помощи соотношения (174). Используя дельта-коррелированность флуктуаций показателя преломления, после вычислений найдем: . (175)
. (175) , (176)
, (176) - поле в плоскости х =0, а подынтегральное выражение в экспоненте представляет величину, входящую в правую часть выражения (173):
- поле в плоскости х =0, а подынтегральное выражение в экспоненте представляет величину, входящую в правую часть выражения (173): . (177)
. (177)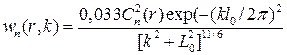 (178)
(178) в следующей форме:
в следующей форме: (179)
(179) , из выражений (176) и (178) получаем:
, из выражений (176) и (178) получаем: (180)
(180) , а в качестве функционала
, а в качестве функционала  взять произведение
взять произведение  .
. . Уравнение, которому удовлетворит
. Уравнение, которому удовлетворит  , тогда примет вид:
, тогда примет вид: (181)
(181)


