
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики излучения в случайно-неоднородной среде с гауссовской функцией корреляцииСодержание книги
Поиск на нашем сайте
Вычисление приведенных интегралов можно осуществить аналитическим путем и сделать ряд заключений, не конкретизируя вида функции Функция корреляции
Несложно получить асимптотические выражения для дисперсий флуктуаций уровня и фазы для двух значений величины D, называемой волновым параметром:
где Рассмотрим случай D >>1. При этом
Таким образом, для случая больших D получили, что флуктуации уровня и фазы одинаковы и растут пропорционально расстоянию до точке приема z, – длине трассы. Пусть теперь D <<1. Тогда
В этом случае средний квадрат случайных вариаций фазы растет пропорционально расстоянию, а средний квадрат флуктуаций уровня – кубу расстояния. Дело в том, что при малых значениях волнового параметра средний размер неоднородностей больше первой зоны Френеля:
Следовательно, в пределах зоны Френеля отклонения показателя преломления имеют один знак. Волны, рассеиваемые отдельными элементами объема, приходят в точку приема в фазе. Вследствие этого флуктуации амплитуды быстро возрастают с увеличением расстояния (пропорционально кубу расстояния). В случае малых по сравнению с зоной Френеля неоднородностей область, формирующая рассеянный сигнал, содержит большое число элементов как с положительными, так и с отрицательными отклонениями показателя преломления от среднего. В результате далеко не все волны, создаваемые отдельными элементами рассеивающего объема, приходят в точку приема в одной или мало отличающихся фазах. Это приводит к их частичной компенсации, в силу чего рост флуктуаций с расстоянием происходит сравнительно медленно, пропорционально расстоянию в первой степени, в соответствии с соотношением (162). Не менее важными, а в большинстве случаев –особенно существенными статистическими характеристиками случайных вариаций уровня и фазы волн, распространяющихся в атмосфере, служат функции или коэффициенты корреляции, представляющие количественную оценку связи одной флуктуирующей величины с другой или двух ее разнесенных во времени или пространстве значений.
Соответствующие функции корреляции для флуктуаций уровня и фазы, а также взаимные корреляции между уровнем и фазой могут быть вычислены с использованием соотношений (157) и (158) как среднее значение произведения двух соответствующих величин. Приведем конечный результат этого вычисления для пространственной функции корреляции флуктуаций показателя преломления в виде гауссоиды. Для больших значений волнового параметра (фактически, для типичных тропосферных трасс) получаем:
Если ввести дополнительное предположение
то вычисления пространственного коэффициента корреляции между величинами фазы и уровня в двух точках, разнесенных вдоль трассы, приводят к следующим соотношениям:
Отсюда легко найти радиус или интервал корреляции, определяемый как расстояние, на котором коэффициент корреляции принимает значение 0,5 (или 1/ e):
Это соотношение показывает, что интервал продольной корреляции уровня и фазы в рассматриваемом случае больших D, когда Соотношения (157) и (158) позволяют получить значения коэффициентов корреляции флуктуаций уровня и фазы при разнесении поперек трассы. При малых D кривая коэффициента корреляции флуктуаций уровня несколько отличается от совпадающих кривых, относящихся к фазе и показателю преломления. Однако интервалы корреляции всех кривых примерно одинаковы. При больших D интервал поперечной корреляции как уровня, так и фазы близок к интервалу поперечной корреляции вариаций показателя преломления в среде. Сравнение с данными по продольному разнесению (168) свидетельствует, что пространственная функция корреляции уровня и фазы поля волны при больших значениях волнового параметра анизотропны даже при изотропном характере флуктуаций показателя преломления. Сильная турбулентность В настоящее время интенсивно развивается теория распространения электромагнитных волн в средах с сильно развитой турбулентностью в применении к пучкам и длинным трассам. Выяснилось, что экспериментальные результаты, полученные на сравнительно длинных трассах, не находят теоретического объяснения в рамках метода плавных возмущений. Было показано, что приближение метода плавных возмущений эквивалентно модели распространения волн в виде случайных фазовых экранов без учета многократного рассеяния на турбулентных неоднородностях. Вызванное этим обстоятельством развитие теории привело к привлечению новых методов (диаграммной техники, теории переноса излучения и других. Среди них значительное внимание было уделено методу параболического уравнения (или марковскому приближению).
Ма́рковский проце́сс — случайный процесс, эволюция которого после любого заданного значения временно́го параметра tt {\displaystyle t} Связь между нормальными и марковскими процессами состоит в том, что они частично пересекаются.
Ограничимся краткими сведениями об основных результатах анализа распространения пучков на длинных трассах. В основу вычислений положим волновое уравнение для среды с переменным показателем преломления
Здесь Представим электрическое поле пучка волн, распространяющихся вдоль оси х, в виде:
Подставляя это выражение в волновое уравнение (169), пренебрежем членом Воспользуемся приближенным равенством Тогда
Это уравнение носит название параболического приближения и описывает распространение пучков в условиях малой угловой расходимости (поскольку мы пренебрегли величиной
В эти выражения входят значения так называемых внутреннего и внешнего размеров неоднородностей и структурной характеристики флуктуаций, характеризующей интенсивность турбулентных возмущений показателя преломления на трассе. Первое из них налагает требование узконаправленности диаграммы рассеяния неоднородностей в направлении распространения. Второе означает пренебрежимо малый уровень рассеяния мощности поля на расстояниях порядка длины волны. Для типичных значений параметров трасс и турбулентности эти условия выполняются в оптическом диапазоне для трасс длиной в сотни километров. От полученного уравнения можно перейти к уравнениям для моментов случайной величины Е разных порядков. Метод такого перехода основан на предположении о дельта-коррелированности флуктуаций показателя преломления Выразим аналитически дельта-коррелированность флуктуаций величины n:
Здесь
Функциона́л — это отображение, заданное на произвольном множестве и имеющее числовую область значений: обычно множество вещественных чисел R {\displaystyle \mathbb {R} } Справка по вариационной производной: Функционал записывается в виде:
Это прямой аналог дифференциала функции конечномерного аргумента ( Производная Фреше, – аналог одномерного градиента, - называется вариационной производной:
Здесь выражение в круглых скобках – скалярное произведение;
Сумма представляет собой полный дифференциал. Если представить
можно записать
Далее воспользуемся соотношением, выражающим корреляцию между нормально распределенной случайной величиной
где через Принимая эти соотношения, мы тем самым приписываем случайной величине Возьмем теперь в качестве функционала
Это уравнение разрешимо относительно первого момента случайного поля
где
Принимая, что
находим интеграл от
Для случая плоской волны, то есть при
Подобная процедура может быть применена и для вычисления других моментов поля. Так, для вывода уравнения, которому удовлетворяет второй момент поля, нужно уравнение (171) умножить на Запишем второй момент флуктуаций поля
Решая это уравнение методом преобразования Фурье, находим:
Здесь
Полученная для
Чтобы рассчитать флуктуации интенсивности, а также ряд других эффектов, возникающих при распространении пучка, требуется получить уравнение для четвертого момента случайного поля:
С помощью аналитической процедуры находим соответствующее уравнение: (185) Для этого уравнения был найден ряд приближенных решен Отметим, что описание сильных флуктуаций проводят на основе подхода, предполагающего вывод и решение уравнений для статистических моментов комплексной амплитуды поля (функций когерентности). Наибольший интерес представляют функции когерентности второго
и четвертого порядков:
Через них выражается средняя интенсивность, степень когерентности, дисперсия флуктуаций интенсивности и коэффициент пространственной корреляции. Здесь комплексная амплитуда А характеризует электромагнитные колебания
а Использование малоуглового приближения, предполагающего рассеяние волны под малыми углами, позволяет заменить оператор на оператор Лапласа, действующий по поперечным координатам. Таким образом получаем исходное уравнение для нахождения функций когерентности. При этом неоднородности показателя преломления в направлении распространения представлены дисками, ориентированными перпендикулярно направлению распространения. Математически это предположение может быть представлено в виде:
Здесь Физически такое представление основывается на том, что, в отличие от корреляции показателя преломления в поперечном направлении его продольная корреляция оказывает лишь малое влияние на флуктуационные характеристики поля. Как результат, корреляция амплитудных флуктуаций в продольном направлении оказывается в большинстве практических случаев существенно больше размеров неоднородностей. Путем преобразований получаем
Здесь
Таким образом, функция когерентности экспоненциально убывает с увеличением расстояния z. Показатель экспоненты определяется структурной функцией комплексной фазы. В условиях сильных флуктуаций дисперсия определяется согласно соотношению
где степень возмущенности трассы оценивается как
Радиус корреляции флуктуаций по пятну в условиях сильных флуктуаций составляет
то есть меньше радиуса первой зоны Френеля.
Лекция 25 октября 2016г.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.78.148 (0.013 с.) |

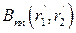 или взяв для нее аппроксимирующую кривую. Не приводя подробных вычислений, сформулируем основные теоретические выводы, вытекающие из конечных соотношений для неоднородностей, характерные линейные размеры которых значительно превышают длину волны
или взяв для нее аппроксимирующую кривую. Не приводя подробных вычислений, сформулируем основные теоретические выводы, вытекающие из конечных соотношений для неоднородностей, характерные линейные размеры которых значительно превышают длину волны 
 (160)
(160) , (161)
, (161) - радиус первой зоны Френеля.
- радиус первой зоны Френеля. (162)
(162) (163)
(163) . (164)
. (164) (165)
(165) .
. , (166)
, (166)
 . (167)
. (167)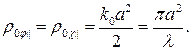 (168)
(168) , значительно превышает интервал корреляции флуктуаций показателя преломления, определяемый размером неоднородностей
, значительно превышает интервал корреляции флуктуаций показателя преломления, определяемый размером неоднородностей  .
. не зависит от эволюции, предшествовавшей tt {\displaystyle t}, при условии, что значение процесса в этот момент фиксировано («будущее» процесса не зависит от «прошлого» при известном «настоящем»; другая трактовка (Вентцель): «будущее» процесса зависит от «прошлого» лишь через «настоящее»).
не зависит от эволюции, предшествовавшей tt {\displaystyle t}, при условии, что значение процесса в этот момент фиксировано («будущее» процесса не зависит от «прошлого» при известном «настоящем»; другая трактовка (Вентцель): «будущее» процесса зависит от «прошлого» лишь через «настоящее»). , случайно меняющимся в пространстве и времени:
, случайно меняющимся в пространстве и времени: . (169)
. (169)
 . (170)
. (170) .
. .
. . (171)
. (171) и другими членами). Условия применимости этого приближения известны и могут быть записаны в виде неравенств:
и другими членами). Условия применимости этого приближения известны и могут быть записаны в виде неравенств: (172)
(172) в направлении распространения. Иными словами, в этом случае неоднородности показателя преломления представляются дисками, ориентированными перпендикулярно направлению распространения. При таком подходе к дальнейшему развитию теории достаточно просто получить ряд полезных отношений.
в направлении распространения. Иными словами, в этом случае неоднородности показателя преломления представляются дисками, ориентированными перпендикулярно направлению распространения. При таком подходе к дальнейшему развитию теории достаточно просто получить ряд полезных отношений. (173)
(173) – пространственный спектр флуктуаций показателя преломления,
– пространственный спектр флуктуаций показателя преломления,  - волновой вектор,
- волновой вектор,  - вектор в плоскости
- вектор в плоскости 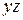 .
.
 ).
).
 - градиент функции y;
- градиент функции y; - оператор частной производной по –ой координате.
- оператор частной производной по –ой координате. .
. - вариационная производная Ф по
- вариационная производная Ф по  .
. в такой форме:
в такой форме: , (174)
, (174) обозначена вариационная производная.
обозначена вариационная производная. . Усредним уравнение (171) и подставим вместо
. Усредним уравнение (171) и подставим вместо  выражение, полученное при помощи соотношения (174). Используя дельта-коррелированность флуктуаций показателя преломления, после вычислений найдем:
выражение, полученное при помощи соотношения (174). Используя дельта-коррелированность флуктуаций показателя преломления, после вычислений найдем: . (175)
. (175) , (176)
, (176) - поле в плоскости х =0, а подынтегральное выражение в экспоненте представляет величину, входящую в правую часть выражения (173):
- поле в плоскости х =0, а подынтегральное выражение в экспоненте представляет величину, входящую в правую часть выражения (173): . (177)
. (177)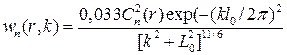 (178)
(178) в следующей форме:
в следующей форме: (179)
(179) , из выражений (176) и (178) получаем:
, из выражений (176) и (178) получаем: (180)
(180) , а в качестве функционала
, а в качестве функционала  взять произведение
взять произведение  .
. . Уравнение, которому удовлетворит
. Уравнение, которому удовлетворит  , тогда примет вид:
, тогда примет вид: (181)
(181)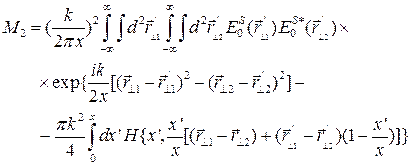 . (182)
. (182) . (183)
. (183)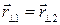 , то перейдем к формуле для интенсивности как функции поперечных координат.
, то перейдем к формуле для интенсивности как функции поперечных координат. (184)
(184) ий, относящихся как к флуктуациям интенсивности, так и к блужданиям пучка, усредняющему действию апертуры и другим эффектам.
ий, относящихся как к флуктуациям интенсивности, так и к блужданиям пучка, усредняющему действию апертуры и другим эффектам. (186)
(186) . (187)
. (187) , (188)
, (188) - составляющая вектора r, лежащая в поперечной плоскости волны, распространяющейся вдоль оси z.
- составляющая вектора r, лежащая в поперечной плоскости волны, распространяющейся вдоль оси z. . (189)
. (189) - функция корреляции флуктуаций показателя преломления,
- функция корреляции флуктуаций показателя преломления,  - функция корреляции флуктуаций показателя преломления в поперечной плоскости,
- функция корреляции флуктуаций показателя преломления в поперечной плоскости,  - дельта-функция.
- дельта-функция. . (190)
. (190) , (191)
, (191) и
и  – соответственно волновое число и энергетический спектр неоднородностей.
– соответственно волновое число и энергетический спектр неоднородностей. , (192)
, (192) , (193)
, (193) - структурная характеристика флуктуаций показателя преломления атмосферы.
- структурная характеристика флуктуаций показателя преломления атмосферы. , (194)
, (194)


