
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотность вероятности и функции распределенияСодержание книги
Поиск на нашем сайте
Вероятность события Р, заключающаяся в том, что наблюдаемая случайная величина меньше или равна допустимому значению х, определяет функцию распределения вероятностей случайной величины Х:
Иногда ее называют интегральной функцией распределения. Введенная таким образом функция распределения F (x) является вещественной функцией, всегда положительной и неубывающей. Кроме того, для реальных процессов эта функция непрерывна и дифференцируема. Хотя функция распределения F (x) и дает исчерпывающее описание вероятностной модели одной случайной величины, ее форма не всегда удобна для проведения необходимых расчетов. В ряде случаев предпочтительнее использовать не саму функции
Ее физический смысл легче раскрыть через элемент вероятности
Из этого выражения следует, что элемент вероятности Мы уже упоминали, что вероятность того, что непрерывно распределенная случайная величина имеет точное значение, равна нулю. По определению вероятности функция распределения нормируется условием:
Поскольку функция Каковы характерные особенности интегральной функции распределения? Пример: Пусть в комнате находится 100 человек разного возраста. Можно составить распределение по возрастам: от 0 до 3 лет, от 3 до 6, и так далее. Ступенчатая картинка такого распределения носит название гистограммы. Огибающей гистограммы будет дифференциальная функция распределения. Интегральная функция распределения говорит о том, какая часть людей, находящихся в комнате, будет иметь возраст от 0 до 3 лет, от 3 до 6 лет и так далее. Эта функция будет возрастать, постепенно достигая насыщения. Основные свойства плотности распределения вероятностей: 1. 2. 3. 4. При анализе стохастических процессов наиболее употребительным является так называемое нормальное (гауссовское) распределение:
где Эта плотность вероятности содержит два параметра, - Подчеркнем особенности нормального закона распределения. 1. Он служит основой для формулировки центральной предельной теоремы: если имеется сумма большого числа независимых случайных величин (измерений), то эта сумма будет распределена по нормальному закону, независимо от законов распределения каждой из этих величин в отдельности. 2. Нормально распределенный процесс характеризуется первыми двумя моментами. Все нечетные моменты для этого закона равны нулю. А четные моменты порядков m >2 полностью определяются через момент второго порядка. 3. Он удобен для вычислений и аппроксимации. В то же время нормальный закон обладает и некоторыми недостатками: 1. Реальные процессы довольно часто бывают асимметричными, то есть преобладают ошибки, б о льшие или меньшие среднего. 2. Реальные процессы не всегда допускают отклонения от 3.Реальные распределения часто имеют больше одного максимума. 4. В ряде случаев распределение по одному параметру отличается от распределения по другому, то есть нормальный закон не всегда универсален. Количественные критерии нормальности распределения. 1. Критерий Анализ показывает, что при 2. Критерий Колмогорова:
Здесь Для оценки поведения интегральных распределений интенсивности в пучках при их различных состояниях часто применяются следующие виды распределений: 1 – нормальное распределение:
2 – экспоненциальное распределение:
3 – нормально-логарифмическое распределение:
В задачах распространения радиоволн в случайно-неоднородной среде под величиной Х понимают такие параметры излучения, как значения интенсивности (амплитуды), фазы, положение центра тяжести лазерного пучка и др. На основе метода плавных возмущений было установлено, что плотность вероятности флуктуаций интенсивности в режиме слабых флуктуаций с хорошим приближением описывается нормально-логарифмическим законом при
где I – локальная интенсивность, При распространении излучения на атмосферных трассах близкими к нормальному распределению оказываются распределения флуктуаций фазы и распределения флуктуаций центра тяжести. Для описания области сильных флуктуаций интенсивности приемлемым оказывается экспоненциальный закон распределения:
Соответствующий релеевскому распределению амплитуды экспоненциальный закон распределения плотности вероятности предполагает статистическую независимость компонент световой волны, рассеянной на турбулентных неоднородностях. Однако для атмосферной турбулентности, где реализуется широкий диапазон масштабов неоднородностей, компоненты рассеянных полей оказываются частично коррелированными за счет крупных неоднородностей. Это приводит к определенному отклонению экспериментальных данных от экспоненциального закона. Учет коррелированности рассеянных компонент поля представляет актуальную проблему для проводимых теоретических исследований. Среди предлагаемых распределений можно выделить так называемое К -распределение. Однако его анализ мы здесь опустим.
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.20.252 (0.01 с.) |

 . (21)
. (21)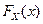 , а ее производную. Эта производная носит название плотности распределения вероятностей (плотности вероятностей или дифференциального распределения):
, а ее производную. Эта производная носит название плотности распределения вероятностей (плотности вероятностей или дифференциального распределения): (22)
(22) . Его можно записать в виде:
. Его можно записать в виде: . (23)
. (23) .
. . (24)
. (24) - это плотность распределения вероятностей, а не сама вероятность, она не обязательно должна быть меньше единицы и может принимать любые неотрицательные значения.
- это плотность распределения вероятностей, а не сама вероятность, она не обязательно должна быть меньше единицы и может принимать любые неотрицательные значения.

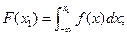
 . (25)
. (25) , (26)
, (26)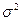 - дисперсия величины х.
- дисперсия величины х. и
и  , - среднее значение и дисперсию случайной величины (см. дальше).
, - среднее значение и дисперсию случайной величины (см. дальше). до
до  .
. : Пусть имеется некоторый случайный процесс. Разобьем его на n интервалов. В каждом i -ом интервале возьмем по
: Пусть имеется некоторый случайный процесс. Разобьем его на n интервалов. В каждом i -ом интервале возьмем по  значений. Предполагаемую вероятность обозначим через
значений. Предполагаемую вероятность обозначим через  .
. функция
функция 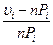 распределена по нормальному закону. Тогда критерий
распределена по нормальному закону. Тогда критерий 
 . (27)
. (27) - экспериментально полученное распределение;
- экспериментально полученное распределение;  - предполагаемое распределение. Эта функция также протабулирована.
- предполагаемое распределение. Эта функция также протабулирована. ; (28)
; (28) ; (29)
; (29) . (30)
. (30) , (31)
, (31) - среднее по времени значение интенсивности. Дополнительные исследования показали, что нормально-логарифмическое распределение может удовлетворительно описывать экспериментальные данные не только при слабых флуктуациях, но и в условиях сильных флуктуаций.
- среднее по времени значение интенсивности. Дополнительные исследования показали, что нормально-логарифмическое распределение может удовлетворительно описывать экспериментальные данные не только при слабых флуктуациях, но и в условиях сильных флуктуаций. (32)
(32)


