
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теоретического анализа флуктуаций параметров излучения в турбулентной атмосфереСодержание книги
Поиск на нашем сайте
Большой круг вопросов, связанных с исследованием закономерностей взаимодействия электромагнитного излучения со средой, показатель преломления которой испытывает хаотические пространственно-временные вариации, требует для своего решения применения аппарата теории случайных процессов. Представим, что отражающая поверхность совершает некоторые движения вверх и вниз. При этом будет меняться разность фаз прямого и отражённого лучей в точке приема. Поскольку незначительные вариации длины пути радиоволны не могут сколько-нибудь значительно повлиять на величину испытываемого в процессе распространения поглощения, амплитуду волны в точке приема можно считать постоянной. Поэтому напряженность поля в точке приема записывают в виде:
где фаза Это позволяет рассматривать приходящий в точку приема сигнал как случайным образом модулированный по фазе. Поскольку, по определению, мгновенная скорость изменения фазы характеризует мгновенное же значение частоты, то
Отсюда
Тогда выражение для амплитуды можно представить в виде
Вычислив производную от показателя экспоненты в этом выражении, находим мгновенное значение принимаемой частоты:
Следовательно, флуктуации длины пути распространяющегося луча можно по желанию толковать либо как случайные флуктуации фазы, либо как случайные флуктуации частоты принимаемого сигнала.
В результате действия множественных рассеивающих объектов, - турбулентностей, - поле в точке приема будет представлять сумму полей постоянных амплитуд и случайным образом меняющихся фаз. Особый интерес при этом представляет распространение в среде со случайно меняющимся показателем преломления. В таких условиях характеристики среды и, соответственно, электромагнитного поля, могут быть описаны лишь на основе статистических представлений. Эти представления основываются на корреляционных связях вариаций поля электромагнитной волны и статистически описываемых изменений показателя преломления. Будем анализировать скалярное волновое уравнение для случайно-неоднородной среды. Рассмотрение этой проблемы представляет, помимо большого теоретического интереса, практически важную задачу о характере флуктуаций поля в зоне прямой видимости или в зоне дифракции, а также при прохождении радиоволн через различные области земной атмосферы, в которые вкраплены хаотически перемещающиеся и изменяющиеся во времени неоднородности. Будем считать, что амплитуда первичного поля значительно больше амплитуды рассеянной компоненты. Эффектами вторичного переизлучения пренебрежем. Пусть на полупространство, заполненное случайными неоднородностями диэлектрической проницаемости, падает плоская электромагнитная волна, направление распространения которой совпадает с осью
Диэлектрическая проницаемость как случайная функция координат и времени может быть определена суммой:
При этом среднее значение диэлектрической проницаемости (при усреднении и по времени, и по координатам)
Большое число измерений, выполненных как при помощи самолетных рефрактометров, так и другими способами, позволили установить приблизительные пределы изменений относительной величины флуктуаций диэлектрической проницаемости:
Знание этой величины позволит сформулировать приближенные уравнения, когда можно пренебречь членами высокого порядка малости. Для рассматриваемого случая уравнения Максвелла имеют вид:
Если скорость флуктуаций ε мала по сравнению со скоростью изменения поля, то есть с частотой волны,
то для тех диапазонов, о которых мы говорим,
Преобразуем эти выражения.
или
Пренебрегаем вторым членом в квадратных скобках, учитывая (113). Тогда уравнение для напряженности поля примет вид:
Не будем рассматривать влияние поляризации волны на характер распространения. Тогда задача сводится к решению скалярного уравнения
где
Волновое уравнение для произвольной компоненты
где показатель преломления есть функция времени и пространственных координат:
Если приращение
При
Уравнение для А можно получить, подставляя это значение в исходное волновое уравнение (120) и учитывая соотношения для величин 1. 2. Средний показатель преломления близок к единице, что характерно для тропосферных трасс. Тогда
и волновое уравнение принимает вид:
Рассмотрим приближенные методы его решения.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.228 (0.007 с.) |

 (105)
(105) – случайная величина.
– случайная величина. . (106)
. (106) . (107)
. (107) . (108)
. (108)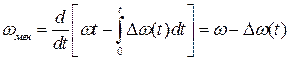 . (109)
. (109) :
: . (110)
. (110) . (111)
. (111) равно единице:
равно единице: . (112)
. (112) . (113)
. (113) . (114)
. (114) , (115)
, (115) . (116)
. (116)
 . (117)
. (117) . (118)
. (118) , (119)
, (119) .
. напряженности электрического (или магнитного) поля излучения в случайно-неоднородной среде имеет вид:
напряженности электрического (или магнитного) поля излучения в случайно-неоднородной среде имеет вид: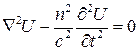 , (120)
, (120) . (121)
. (121) , одним из решений уравнения будет плоская волна, распространяющаяся, например, в направлении положительных z:
, одним из решений уравнения будет плоская волна, распространяющаяся, например, в направлении положительных z: . (122)
. (122) решение уравнения (120) представимо в виде квазиплоской волны, амплитуда А которой зависит от координат:
решение уравнения (120) представимо в виде квазиплоской волны, амплитуда А которой зависит от координат: . (123)
. (123) . При этом используют следующие предположения:
. При этом используют следующие предположения: . Это означает, что за период колебания в рассматриваемом диапазоне частот амплитуда не испытывает заметного изменения.
. Это означает, что за период колебания в рассматриваемом диапазоне частот амплитуда не испытывает заметного изменения.
 . (124)
. (124)


