
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лучевое приближение (метод геометрической оптики)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В этом случае считаем
Тогда волновое уравнение имеет решением следующую функцию:
где Это приближение, дающее решение в виде плоских волн, то есть оставляющее только лучевую трактовку распространения, естественно, не учитывает явления дифракции. Однако, в случаях, когда оптическая длина пути велика, дифракционный эффект значителен и пренебрежение членом Метод малых возмущений (борновское приближение) Если состояние среды таково, что неоднородности вносят малые возмущения в величину A, то приближенное решение волнового уравнения (124) можно получить методом последовательных приближений:
откуда получим
В этом разложении каждое слагаемое Если последующие слагаемые малы по сравнению с предыдущими относительного вклада членов ряда, ответственных за многократное рассеяние. Нулевой член ряда описывает падающую на среду (или невозмущенную) волну, слагаемое первого порядка – однократно рассеянное поле, второго порядка – двукратно рассеянное и т. д. Многократное рассеяние, как правило, становится существенным при возрастании интенсивности флуктуаций показателя преломления либо за счет возрастания В первом приближении, называемом борновским,
Подставляя это значение в исходное волновое уравнение, получаем:
Чтобы найти
Определяя из этого выражения
Решение этого уравнения известно:
где Записав
Равенство (134) показывает, что поле рассеянной волны, наблюдаемое в точке r, обусловлено сферической волной, излучаемой из точки r ’, а именно Согласно (128), имеем:
Для малых углов рассеяния, то есть малых отклонений координат от оси z, величину q можно разложить в ряд:
где векторы Тогда из (135) получаем:
Интересная особенность формулы (137) заключается в том, что она содержит информацию о положении и форме интерференционных полос (пятен) на расстоянии z в плоскости наблюдения. Эти полосы возникают за счет взаимодействия падающей плоской волны с рассеянной сферической волной, переизлученной из точки На практике Для сантиметровых и более коротких волн представляет интерес решение этого уравнения для случая крупных неоднородностей. Метод Рытова (метод плавных возмущений, МПВ) Вспомним, что напряженность электрического поля для однородной среды из уравнения (120) запишется в виде:
В случае неоднородной среды с диэлектрической проницаемостью, являющейся функцией координат, решением будет аналогичная функция, но с амплитудой и фазой, зависящими от координат в виде:
Не рассматривая изменения неоднородностей во времени, т.е. полагая, как и прежде, квазистатичность задачи, координатную часть
где Для атмосферы Приведенное уравнение для U получено из исходного волнового уравнения (120) путем подстановки:
Метод решения этого уравнения, предложенный С.М.Рытовым, состоит в том, что координатная часть компоненты поля ищется в виде:
Функция
Поскольку Сравнивая эти два представления, находим:
или
где Логарифм отношения амплитуд Обозначим
Подставляя это выражение в уравнение для
Решая это уравнение методом малых возмущений, мы налагаем требование малости на Найдем уравнение для первого приближения (пренебрегая эффектами вторичного рассеяния):
Величину
Подстановка (146) в уравнение для
получаем уравнение для функции
Для плавных возмущений можно пренебречь членами порядка
Тогда
Рассматривая падение плоской волны на среду со случайными неоднородностями, находящимися в полупространстве
совпадающее со (130) с точностью до мнимой единицы и знака правой части. Заметим, что пренебрежение членом Решение этого уравнения будем искать в виде:
где вспомогательная функция Подставляя соответствующие значения для параметров
или
Решение неоднородного уравнения (151) по аналогии с решением уравнения (137) дает следующее выражение для
Оно позволит оценить характеристики флуктуаций. Флуктуации уровня и фазы Амплитудно-фазовые флуктуации в случайно-неоднородной среде принято описывать величиной Следует отметить, что Выделим в выражении (152) действительную и мнимую части:
Отсюда на основании (143) находим:
Эти формулы выражают флуктуации фазы и уровня в среде со случайными неоднородностями. Они справедливы приближенно при упомянутом выше условии:
Учитывая статистический характер флуктуаций показателя преломления
Это неравенство эквивалентно соотношениям:
Первое из этих соотношений справедливо, если рассеяние мало на расстояниях порядка длины волны, т.е. уровень сигнала на этих расстояниях сохраняется почти постоянным. Второе неравенство (156) требует малости изменения угла отклонения луча от первоначального направления. Поскольку
Аналогично,
Следовательно,
то есть все поперечные компоненты градиента фазы малы по сравнению с продольной составляющей. Иными словами, угол отклонения луча от первоначального направления мал. Первое из условий (156) в реальных случаях земной атмосферы выполняется во всех случаях, когда флуктуации показателя преломления малы. Второе условие осуществимо в тех случаях, когда размеры неоднородностей велики по сравнению с длиной волны, поскольку мелкомасштабные неоднородности создают изотропное рассеяние, а крупные переизлучают в пределах узкого конуса в направлении распространения. Угол раствора конуса пропорционален 1/ ka. При этом отклонение луча от первоначального направления будет малым, если амплитуда рассеянной волны значительно меньше амплитуды падающей волны. Для волн оптического диапазона тропосферные неоднородности представляют неоднородности больших размеров. Это означает, что полученные выше результаты служат важной теоретической основой исследования вариаций поля оптической волны, распространяющейся в реальных условиях вблизи земной поверхности. Учитывая малость углов отклонения от направления волны, падающей на среду с неоднородностями, можно считать, что в формулах (154)
при Используя выражение для q (136), запишем:
Лекция 18 октября 2016 г.
Таким образом, получаем выражения для флуктуаций уровня и фазы в малоугловом приближении:
Эти формулы позволяют найти основные статистические параметры, характеризующие вариации уровня и фазы волны, распространяющейся в среде со случайными неоднородностями. Пусть прием ведется в точке
(159)
Здесь
- коэффициент корреляции случайных изменений Как свидетельствуют соотношения (159), средние квадраты флуктуаций фазы и уровня определяются видом корреляционной функции флуктуаций показателя преломления. Последняя в свою очередь зависит от конкретных свойств среды распространения. При практическом использовании результатов, полученных методом плавных возмущений, отметим, что с точки зрения сделанных при его обосновании допущений он применим лишь для малых флуктуаций уровня и фазы. Однако рядом исследователей установлено, что указанные условия следует рассматривать как достаточные, но не необходимые. Было показано, что в части, относящейся к флуктуациям фазы, метод справедлив практически для любой наблюдаемой в эксперименте величины фазовых флуктуаций. Что же касается флуктуаций уровня, то метод дает заметные ошибки при
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 611; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.123.41 (0.012 с.) |

 . (125)
. (125)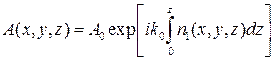 , (126)
, (126) - значение амплитудной функции при
- значение амплитудной функции при 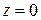 .
. в (124) недопустимо.
в (124) недопустимо.
 . (127)
. (127) имеет порядок малости
имеет порядок малости  .
. , конечное число членов ряда будет достаточным для описания поля волны. К сожалению, такая ситуация имеет место не во всех случаях, члены ряда могут возрастать. Физически это связано с увеличением
, конечное число членов ряда будет достаточным для описания поля волны. К сожалению, такая ситуация имеет место не во всех случаях, члены ряда могут возрастать. Физически это связано с увеличением , либо из-за увеличения пути, проходимого излучением в среде. В результате интегральное изменение показателя преломления вдоль трассы существенно возрастает. Рассмотрим задачу в приближении однократного рассеяния.
, либо из-за увеличения пути, проходимого излучением в среде. В результате интегральное изменение показателя преломления вдоль трассы существенно возрастает. Рассмотрим задачу в приближении однократного рассеяния.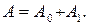 (128)
(128)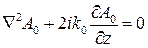 , (129)
, (129) (130)
(130) , нужно решить линейное неоднородное уравнение второго порядка (130). Для этого вводят новую функцию координат
, нужно решить линейное неоднородное уравнение второго порядка (130). Для этого вводят новую функцию координат 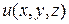 :
: . (131)
. (131) и подставляя их в уравнение (130), получим, положив для случая падения плоской волны на плоскую границу среды
и подставляя их в уравнение (130), получим, положив для случая падения плоской волны на плоскую границу среды  , следующее уравнение:
, следующее уравнение: . (132)
. (132) , (133)
, (133) и
и  - координаты точки наблюдения и источника вторичных волн,
- координаты точки наблюдения и источника вторичных волн,  .
. , получаем:
, получаем: . (134)
. (134) . Амплитуда сферической волны пропорциональна произведению локального значения флуктуирующей части показателя преломления
. Амплитуда сферической волны пропорциональна произведению локального значения флуктуирующей части показателя преломления  и напряженности поля падающего излучения. А фаза определяется общим числом длин волн, укладывающихся на пути от источника до рассеивателя и далее до приемника. Вклады всех точек
и напряженности поля падающего излучения. А фаза определяется общим числом длин волн, укладывающихся на пути от источника до рассеивателя и далее до приемника. Вклады всех точек  , находящихся в объеме рассеяния
, находящихся в объеме рассеяния  , суммируются.
, суммируются. . (135)
. (135)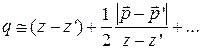 , (136)
, (136) и
и  располагаются в поперечной плоскости, а их разность означает разность поперечных координат.
располагаются в поперечной плоскости, а их разность означает разность поперечных координат. (137)
(137) . Именно это приводит к флуктуациям амплитуды и фазы, наблюдаемым при распространении излучения, в частности, оптического, в атмосфере.
. Именно это приводит к флуктуациям амплитуды и фазы, наблюдаемым при распространении излучения, в частности, оптического, в атмосфере. часто существенно отличается от
часто существенно отличается от  .
. .
. компоненты поля
компоненты поля  можно описать при помощи приведенного волнового уравнения (уравнения Гельмгольца):
можно описать при помощи приведенного волнового уравнения (уравнения Гельмгольца): , (138)
, (138) - случайная функция координат.
- случайная функция координат. .
. (139)
(139) . (140)
. (140) , называемая комплексной фазой, включает и собственно фазу, и величину, определяющую амплитуду, - так называемый уровень. Иногда используется представление
, называемая комплексной фазой, включает и собственно фазу, и величину, определяющую амплитуду, - так называемый уровень. Иногда используется представление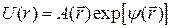 . (141)
. (141) (142)
(142) , (143)
, (143) представляет фазу
представляет фазу  называется уровнем поля и характеризует относительную амплитуду поля. Введя таким образом функцию
называется уровнем поля и характеризует относительную амплитуду поля. Введя таким образом функцию 
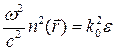 . (144)
. (144) :
: . (145)
. (145) , а не на саму функцию
, а не на саму функцию 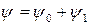 . (146)
. (146) определим из уравнения для
определим из уравнения для  как решение в виде плоской волны:
как решение в виде плоской волны: . (147)
. (147)

 Поскольку
Поскольку 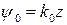 является решением уравнения для
является решением уравнения для 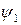 :
: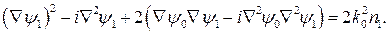 (148)
(148) как квадратами малой величины. Из (147) следует
как квадратами малой величины. Из (147) следует . (148)
. (148) (149)
(149) , будем считать
, будем считать  . Тогда получаем уравнение
. Тогда получаем уравнение (150)
(150) по сравнению с
по сравнению с  может оказаться неправомерным. Поэтому возможность такого приближения нужно рассматривать в сочетании с объектом исследования. Если же оба члена
может оказаться неправомерным. Поэтому возможность такого приближения нужно рассматривать в сочетании с объектом исследования. Если же оба члена  ,
, - медленно меняющаяся функция координат
- медленно меняющаяся функция координат  .
. :
:
 . (151)
. (151) . (152)
. (152) , характеризующей отклонение фазы световых колебаний от фазы плоской однородной волны, и величиной
, характеризующей отклонение фазы световых колебаний от фазы плоской однородной волны, и величиной  , определяющей флуктуации уровня сигнала.
, определяющей флуктуации уровня сигнала.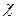 отличается от флуктуаций амплитуды
отличается от флуктуаций амплитуды  , где A – средняя амплитуда. Величина χ отличается и от флуктуаций логарифма амплитуды
, где A – средняя амплитуда. Величина χ отличается и от флуктуаций логарифма амплитуды  . Однако при
. Однако при  можно приближенно считать
можно приближенно считать  .
. . (153)
. (153)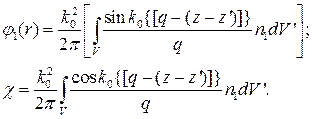 (154)
(154)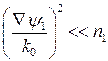 .
. (155)
(155) . (156)
. (156) , получаем:
, получаем:



 .
.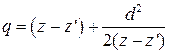 ,
,
 (157)
(157) (158)
(158) . Найдем средние квадраты случайных величин
. Найдем средние квадраты случайных величин  :
:

 Таким образом, метод плавных возмущений позволяет осуществлять оценки в весьма широком диапазоне амплитудно-фазовых флуктуаций.
Таким образом, метод плавных возмущений позволяет осуществлять оценки в весьма широком диапазоне амплитудно-фазовых флуктуаций.


