
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование усиления в электронных приборах в трехволновом приближенииСодержание книги
Поиск на нашем сайте
ЛАБОРАТОРНАЯ РАБОТА №1 Исследование усиления в электронных приборах в трехволновом приближении Цель работы Численно на ЭВМ решается характеристическое алгебраическое уравнение третьей степени с комплексными коэффициентами и находятся постоянные распространения связанных волн в трехволновом приближении. Определяется область усиления в зависимости от параметров электронного потока и резонансной замедляющей системы.
Теорема о сохранении кинетической мощности Выражения для электромагнитной мощности, переносимой полем в замедляющей системе в направлении продольной оси, получается интегрированием вектора Умова-Пойнтинга в приближении малого сигнала по поперечному сечению пучка и структуры. Это выражение эквивалентно уравнению Кинетическая мощность, переносимая пучком при отсутствии замедляющей системы, определяется следующим соотношением Знак минус перед | a 2–|2 имеет следующий физический смысл. Мощность, переносимая быстрой волной пространственного заряда, представляет собой положительную кинетическую мощность, а мощность, переносимая медленной волной – отрицательную кинетическую мощность. Это означает, что в среднем электронный пучок при возбуждении в нем быстрой волны содержит электроны с большей кинетической энергией по сравнению с невозбужденным пучком. Аналогично электронный поток, если в нем возбуждена медленная волна, в среднем содержит электроны с меньшей кинетической энергией по сравнению с невозбужденным пучком. В случае приближения слабой связи, мощностью, обусловленной взаимной связью пучка с полем ЗС, можно пренебречь, тогда полная мощность связанной системы равна
P = Pл + PП = 2 (| a 1+|2 – | a 1–|2 + | a 2+|2 – | a 2–|2) (9)
Продифференцировав по z уравнение (8) и используя уравнения (3) для ЛБВ или уравнения (8), можно показать, что dP/dz = 0, т.е. полная мощность не изменяется вдоль линии. Равенство P = const представляет собой теорему о сохранении кинетической мощности в системе.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ПРОЕКТИРОВАНИЕ МОЩНЫХ МИКРОВОЛНОВЫХ ЭЛЕКТРОННЫХ ПРИБОРОВ С ПРОДОЛЬНЫМ ВЗАИМОДЕЙСТВИЕМ Цель работы Проводится математическое моделирование и проектирование мощных микроволновых электронных приборов с продольным взаимодействием на основе метода крупных частиц. Используется метод крупных частиц в приближении одномерной дисковой модели. Исследуются процессы группирования электронов при изменении параметров скоростной модуляции высокочастотного поля и пространственного заряда электронного пучка. Анализируются нелинейные процессы в мощных электронных приборах с продольным взаимодействием. Осуществляется моделирование и проектирование электронных приборов (ЭП) и определяются их оптимальные конструктивные параметры. Возбуждение поля замедляющей системы электронным потоком Вывод уравнения возбуждения Для вывода уравнения возбуждения электромагнитного поля используем радиофизические аналогии. Представляем спиральную замедляющую систему в виде линии передачи, для которой известны телеграфные уравнения. Из теории длинных линий известно, что любую сложную замедляющую систему с положительной или отрицательной дисперсией волны основной пространственной гармоники можно описать цепочкой связанных многополюсников, сводимых к эквивалентным схемам. Следовательно, любую сложную замедляющую систему и адекватную ей эквивалентную схему можно привести к своему прототипу - фильтру нижних или верхних частот с положительной или отрицательной дисперсией. Используем одночастотное приближение, то есть в приборах происходит усиление сигнала на частоте w. Считаем справедливым одномодовое приближение, то есть возбуждается основной тип волны. Эквивалентная схема линии с потерями состоит из последовательной индуктивности L, последовательного сопротивления R, обусловленного потерями в линии, параллельной емкости С и параллельной проводимости G, обусловленной потерями в диэлектрике. Указанные величины берутся из расчета на единицу длины. В общем случае для определения параметров эквивалентной схемы через геометрические размеры и диэлектрические свойства реальной линии необходимо решать уравнения Максвелла.
В дальнейшем будем пренебрегать потерями в линии. Запишем телеграфные уравнения для стандартной линии передачи, представляющей спиральную замедляющую систему с положительной дисперсией. Электронный поток возбуждает вихревое поле замедляющей системы, вследствие чего в структуре появляется наведенный ток (ток смещения), текущий от электронного пучка в замедляющую систему iнав= iсм=
где Iл и Uл - комплексные амплитуды тока и напряжения в линии передачи, i1 - комплексная амплитуда первой гармоники тока пучка на частоте сигнала w. Проведя несложные преобразования из уравнений (1) получаем дифференциальное уравнение второго порядка относительно напряжения в линии передачи:
где В дальнейшем предполагаем, что индуктивность и емкость линии передачи подобраны таким образом, что выполняется эквивалентность высокочастотного поля и напряжения в линии передачи, то есть выполняется следующее соотношение
Подставим соотношение (3) в уравнение (2) и, продифференцировав левую и правую части уравнения (2), получим следующее уравнение:
где параметр k - коэффициент связи, описывающий связь поля замедляющей системы с электронным пучком. Предположим, что ток электронного потока изменяется по следующему закону:
где Используя соотношение (5), запишем уравнение (4) в виде уравнения возбуждения электромагнитного поля замедляющей системы электронным потоком:
Расчет кулоновских сил. Расчет сил пространственного заряда электронного пучка является наиболее сложной задачей нелинейной теории. Будем использовать приближение эквивалентного гладкого волновода, приближение узких зазоров для многорезонаторных клистронов, квазистатическое и квазипериодическое приближения в МКЧ. В нелинейной теории ЭП применяются различные методы расчета поля пространственного заряда, из которых наиболее распространены следующие: метод функций Грина, метод преобразования Фурье и метод конечных разностей. Нами в данной работе будет использоваться метод функций Грина. Продольная составляющая электрического поля Ez в правой части уравнения движения состоит из двух слагаемых - Ezл - поля замедляющей системы и Ezе - собственного поля электронного пучка (кулоновское поле или поле сил пространственного заряда). В квазистатическом приближении для определения собственного электрического поля необходимо решить уравнение Пуассона Dj = -r / e 0 и найти потенциал j квазистатического электромагнитного поля, после чего определяется кулоновское поле Eze=-grad j, где r - плотность заряда электронного пучка, e 0 - диэлектрическая постоянная активной среды. Из электродинамики известно решение уравнения Пуассона для эквивалентной гладкой трубы дрейфа, в которой движется электронный поток, выражаемое с помощью функции Грина. Поэтому мы сразу выпишем готовое решение для кулоновского поля
где f (z,z’) - это усредненная функция Грина (функция влияния), описывающая действие кулоновских сил со стороны диска в сечении z на диск в сечении z’, Eze- усредненная напряженность электрического поля, действующая на сечение z’ со стороны всех других сечений пучка слева и справа. Запишем аналитическое выражение для усредненной функции Грина, представляемой в виде экспоненциальной функции,
где rп - радиус электронного пучка,
Перейдем во введенную нами ранее фазовую систему координат Лагранжа, тогда соотношение (24) для усредненной функции Грина в движущейся системе координат вместе с электронным потоком примет следующий вид:
где k=2/berп - параметр убывания кулоновских сил с расстоянием, используемый в нелинейной теории, DФ=Ф-Ф’.
ЛАБОРАТОРНАЯ РАБОТА №1 Исследование усиления в электронных приборах в трехволновом приближении Цель работы Численно на ЭВМ решается характеристическое алгебраическое уравнение третьей степени с комплексными коэффициентами и находятся постоянные распространения связанных волн в трехволновом приближении. Определяется область усиления в зависимости от параметров электронного потока и резонансной замедляющей системы.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 74; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.229.1 (0.01 с.) |

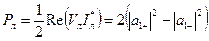 , которое представляет собой мощность, переносимую волнами замедляющей системы при отсутствии пучка. Знак минус показывает, что поток мощности обратной волны a 1– противоположен потоку мощности прямой волны a 1+. Мощность, переносимая каждой из этих волн сохраняется.
, которое представляет собой мощность, переносимую волнами замедляющей системы при отсутствии пучка. Знак минус показывает, что поток мощности обратной волны a 1– противоположен потоку мощности прямой волны a 1+. Мощность, переносимая каждой из этих волн сохраняется. , в то время как кинетическая мощность постоянной составляющей электронного пучка равна P 0 = I 0 V 0.
, в то время как кинетическая мощность постоянной составляющей электронного пучка равна P 0 = I 0 V 0. . Уравнения длинной линии передачи с учетом электронного пучка имеют следующий вид:
. Уравнения длинной линии передачи с учетом электронного пучка имеют следующий вид: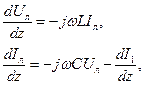 (1)
(1) (2)
(2)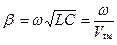 - постоянная распространения прямой бегущей волны в линии передачи; L и C - погонные индуктивность и емкость эквивалентной линии передачи, Vф - фазовая скорость распространения прямой бегущей волны.
- постоянная распространения прямой бегущей волны в линии передачи; L и C - погонные индуктивность и емкость эквивалентной линии передачи, Vф - фазовая скорость распространения прямой бегущей волны. (3)
(3)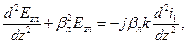 (4)
(4) , тогда получаем выражение:
, тогда получаем выражение: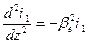 , (5)
, (5)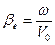 - постоянная распространения электронного пучка, V 0 - постоянная составляющая скорости электронного пучка.
- постоянная распространения электронного пучка, V 0 - постоянная составляющая скорости электронного пучка. . (6)
. (6) (23)
(23)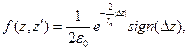 (24)
(24) , Dz=z-z’.
, Dz=z-z’. (25)
(25)


