
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи и метод крупных частицСодержание книги
Поиск на нашем сайте
Математическое моделирование на ЭВМ процессов взаимодействия высокочастотного поля с электронным пучком является одним из наиболее эффективных методов исследования и проектирования электронных приборов. Наиболее общим и широко применяемым методом решения задач нелинейной электроники является метод крупных частиц (МКЧ), позволяющий анализировать тонкую структуру электронных пучков и активных сред, а также исследовать движение отдельных укрупненных частиц в переменных Лагранжа. В данной работе мы рассмотрим основные понятия и идеи МКЧ применительно к задачам нелинейной электроники, причем ограничимся вариантом МКЧ, относящимся к анализу нелинейных одномерных процессов взаимодействия пучка с полем в электронных приборах с продольным взаимодействием, в частности в многорезонаторных клистронах и ЛБВ на цепочках связанных резонаторов (ЦСР). Методы решения задач на ЭВМ в значительной мере зависят от режимов работы ЭП и от типов взаимодействия пучка с полем в приборах. Процессы взаимодействия в электронных приборах можно разделить на две большие группы: - линейные процессы (режим слабого сигнала) - нелинейные эффекты являются слабыми и их можно не учитывать. В этом случае обычно используются линейные теории, основанные на гидродинамических моделях с использованием координат Эйлера (макроскопический подход в теории - усредненное макроскопическое описание вещества). Линейная теория позволяет найти постоянные распространения волн в приборах и определить усиление в ЭП, однако она не учитывает сильных возмущений электронного пучка, приводящих к получению режима насыщения, образованию плотных сгустков, появлению гармоник тока пучка. - нелинейные процессы (режим большого сигнала) - развиваются сильные возмущения электронного пучка, приводящие к нелинейным эффектам, которые необходимо учитывать в теории. В этом случае в нелинейной теории ЭП используется другой подход в теории, основанный на микроскопическом описании электронных пучков и использовании МКЧ с координатами Лагранжа, позволяющий учитывать нелинейные эффекты. Отметим, что основная тенденция в развитии современных ЭП - это увеличение выходной мощности, КПД, тока и напряжения пучка, а это приводит к увеличению нелинейных явлений, которые необходимо учитывать в теории. Основная задача нелинейной теории ЭП состоит в решении самосогласованной системы уравнений электродинамики и электроники, описывающих движение электронного пучка в электромагнитных полях замедляющей системы, и определении выходных параметров ЭП - КПД, выходной мощности, коэффициента усиления и т.д. Прямое решение общей системы уравнений электродинамики и электроники даже при наличии самых мощных и быстродействующих ЭВМ с вычислением траекторий каждого отдельного электрона практически невозможно, что связано с тремя основными существующими проблемами или трудностями: - большим числом электронов в электронном пучке, что приводит к необходимости одновременного решения такого же большого числа уравнений движения; – резким изменением микроскопического поля около точечных электронов; - сложностью краевых и граничных условий реальных замедляющих систем и электронных приборов, что не позволяет дать прямого расчета полного поля, возбуждаемого в замедляющей системе электронным пучком. В преодолении первых двух трудностей как раз и состоит основная идея метода крупных частиц. В МКЧ вместо слежения за каждым отдельным электроном в микроскопическом поле рассматривается движение отдельных укрупненных (крупных) частиц различной формы в макроскопическом поле, причем каждой крупной частице приписывается заряд и масса некоторого объема (облака) окружающих ее электронов. Таким образом, в МКЧ участок электронного пучка длиной в электронную (замедленную) длину волны разбивается (разрезается) на некоторое конкретное дискретное число крупных частиц, движение которых в дальнейшем изучается. При таком разбиении электронного пучка на конечное число крупных частиц возникает ряд вопросов, на которые необходимо ответить теории: - как определить и оценить основные параметры, которые будут характеризовать частотные, временные и пространственные масштабы математических моделей? - как выбрать нужное число крупных частиц и как определить их форму для правильного описания процессов взаимодействия? - каким образом уменьшить ближние (парные) взаимодействия крупных частиц, т.е. как проводить процедуру усреднения микроскопических функций взаимодействия? - каким образом наиболее точно вычислять силы пространственного заряда электронного пучка? - какие процессы в электронных пучках и приборах можно рассматривать с удовлетворительной точностью при выбранных правилах разбиения пучка на крупные частицы?
Возбуждение поля замедляющей системы электронным потоком Вывод уравнения возбуждения Для вывода уравнения возбуждения электромагнитного поля используем радиофизические аналогии. Представляем спиральную замедляющую систему в виде линии передачи, для которой известны телеграфные уравнения. Из теории длинных линий известно, что любую сложную замедляющую систему с положительной или отрицательной дисперсией волны основной пространственной гармоники можно описать цепочкой связанных многополюсников, сводимых к эквивалентным схемам. Следовательно, любую сложную замедляющую систему и адекватную ей эквивалентную схему можно привести к своему прототипу - фильтру нижних или верхних частот с положительной или отрицательной дисперсией. Используем одночастотное приближение, то есть в приборах происходит усиление сигнала на частоте w. Считаем справедливым одномодовое приближение, то есть возбуждается основной тип волны. Эквивалентная схема линии с потерями состоит из последовательной индуктивности L, последовательного сопротивления R, обусловленного потерями в линии, параллельной емкости С и параллельной проводимости G, обусловленной потерями в диэлектрике. Указанные величины берутся из расчета на единицу длины. В общем случае для определения параметров эквивалентной схемы через геометрические размеры и диэлектрические свойства реальной линии необходимо решать уравнения Максвелла. В дальнейшем будем пренебрегать потерями в линии. Запишем телеграфные уравнения для стандартной линии передачи, представляющей спиральную замедляющую систему с положительной дисперсией. Электронный поток возбуждает вихревое поле замедляющей системы, вследствие чего в структуре появляется наведенный ток (ток смещения), текущий от электронного пучка в замедляющую систему iнав= iсм=
где Iл и Uл - комплексные амплитуды тока и напряжения в линии передачи, i1 - комплексная амплитуда первой гармоники тока пучка на частоте сигнала w. Проведя несложные преобразования из уравнений (1) получаем дифференциальное уравнение второго порядка относительно напряжения в линии передачи:
где В дальнейшем предполагаем, что индуктивность и емкость линии передачи подобраны таким образом, что выполняется эквивалентность высокочастотного поля и напряжения в линии передачи, то есть выполняется следующее соотношение
Подставим соотношение (3) в уравнение (2) и, продифференцировав левую и правую части уравнения (2), получим следующее уравнение:
где параметр k - коэффициент связи, описывающий связь поля замедляющей системы с электронным пучком. Предположим, что ток электронного потока изменяется по следующему закону:
где Используя соотношение (5), запишем уравнение (4) в виде уравнения возбуждения электромагнитного поля замедляющей системы электронным потоком:
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.212.225 (0.01 с.) |

 . Уравнения длинной линии передачи с учетом электронного пучка имеют следующий вид:
. Уравнения длинной линии передачи с учетом электронного пучка имеют следующий вид: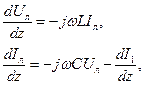 (1)
(1) (2)
(2)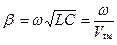 - постоянная распространения прямой бегущей волны в линии передачи; L и C - погонные индуктивность и емкость эквивалентной линии передачи, Vф - фазовая скорость распространения прямой бегущей волны.
- постоянная распространения прямой бегущей волны в линии передачи; L и C - погонные индуктивность и емкость эквивалентной линии передачи, Vф - фазовая скорость распространения прямой бегущей волны. (3)
(3)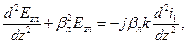 (4)
(4) , тогда получаем выражение:
, тогда получаем выражение: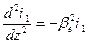 , (5)
, (5)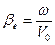 - постоянная распространения электронного пучка, V 0 - постоянная составляющая скорости электронного пучка.
- постоянная распространения электронного пучка, V 0 - постоянная составляющая скорости электронного пучка. . (6)
. (6)


