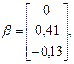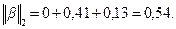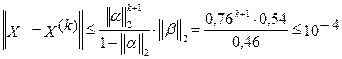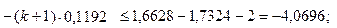Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод последовательных приближений (метод итерации)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть дана система линейных уравнений
Запишем систему (1) в матричном виде: AX=B, где А= Предполагая, что диагональные элементы aii
Обозначим
Система (3') называется системой, приведенной к нормальному виду. Введя обозначения.
Запишем систему (3’) в матричной форме:
или
Решим систему (4) методом последовательных приближений. За нулевое приближение примем столбец свободных членов:
далее, построим матрицы-столбцы
и т.д. Вообще, любое (k +1)-e приближение вычисляют по формуле
X(k+1)=
Если последовательность приближений X (0), X (1),…, X (k) имеет предел
Пример 1. Методом последовательных приближений решить систему
Решение. 1) Приведём данную систему к нормальному виду.
2) Строим последовательные приближения. Нулевое приближение.
Первое приближение.
Второе приближение.
Третье приближение.
Таким образом, x 1=2,9935; x 2=1,0068; x 3=1,0068 и с точностью до 10-1 поучаем x 1=3; x 2=1; x 3=1.
Пример 2. Методом итерации решить следующую систему с точностью до 10-3.
Решение. 1) Приведём данную систему к нормальному виду или
Заметим, что линейную систему можно привести к нормальному виду также следующим образом: записать коэффициенты при x 1, x 2, x 3 в соответствующих уравнениях системы (*) в виде kx, где k - число, близкое к коэффициенту при соответствующем неизвестном и на которое легко разделить коэффициенты при неизвестных и свободные члены. Например: Перепишем систему (*) таким образом: Матрица
2) Последовательно находим
Таким образом, с точностью до 10-3 получаем x 1=0,236; x 2=1,103; x 3= -0,214.
УСЛОВИЯ СХОДИМОСТИ ИТЕРАЦИОННОГО ПРОЦЕССА Пусть дана приведённая к нормальному виду система линейных уравнений Х = Следовательно, условия сходимости можно записать так:
Пример 1. Для системы Итерационный процесс сходится, так как
Аналогично можно было бы проверить выполнение условия сходимости, взяв суммы модулей элементов строк. Процесс итерации заведомо сходится, если элементы матрицы Сходимость итерационного процесса связана нормами матрицы либо либо то процесс итерации линейной системы сходится к единственному решению.
Так, в рассмотренном выше примере норма т.е. итерационный процесс сходится.
ОЦЕНКА ПОГРЕШНОСТИ ПРИБЛИЖЕННОГО ПРОЦЕССА МЕТОДА ИТЕРАЦИИ Если задана допустимая погрешность вычислений где
Пример 1. Показать, что для системы
итерационный процесс сходится, и определить, сколько итераций следует выполнить, чтобы найти корни системы с точностью до 10-4.
Решение. 1) Приводим систему к нормальному виду или
2) Матрица системы
Используя норму 3) Имеем 4) Применяем формулу (1), находим Теоретическая оценка числа итерации, необходимых для обеспечения заданной точности, практически оказывается завышенной.
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 683; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 (1)
(1)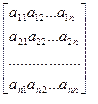 , X=
, X=  , B=
, B=  . (2)
. (2) 0 (i =1, 2,…, n),выразим x 1 через первое уравнение системы, x 2- через второе уравнение и т.д. В результате получим систему, эквивалентную системе (1):
0 (i =1, 2,…, n),выразим x 1 через первое уравнение системы, x 2- через второе уравнение и т.д. В результате получим систему, эквивалентную системе (1):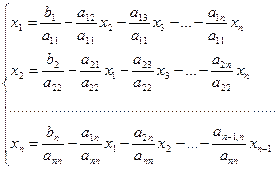 (3)
(3) , где i =1, 2,…, n; j =1, 2,…, n. Тогда система (3) запишется таким образом:
, где i =1, 2,…, n; j =1, 2,…, n. Тогда система (3) запишется таким образом: (3')
(3') ,
,  ,
,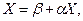
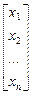 =
= 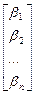 +
+ 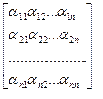 ∙
∙ 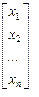 . (4)
. (4) = -
= -  нулевое приближение,
нулевое приближение,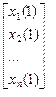 =
=  +
+  ∙
∙ 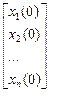 - первое приближение;
- первое приближение;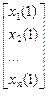 - второе приближение.
- второе приближение. +
+  X(k) (k=0, 1,…, n). (5)
X(k) (k=0, 1,…, n). (5) , то этот предел является решением системы (3), поскольку по свойству предела
, то этот предел является решением системы (3), поскольку по свойству предела  , т.е.
, т.е.  .
.
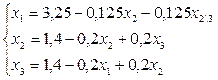
 ,
,  .
. .
. +
+  ∙
∙ 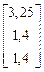 =
= 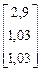
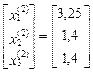 +
+  ∙
∙  =
= 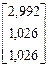
 +
+ 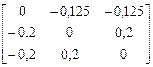 ∙
∙  =
= 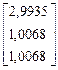

 или
или 

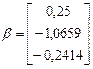

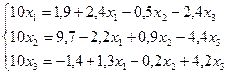

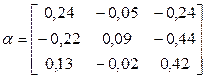
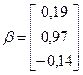
 ,
, +
+  ∙
∙ 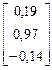 =
=  ,
,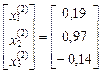 +
+ 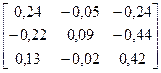 ∙
∙  =
=  .
. следующим образом: если сумма модулей элементов строк или сумма модулей элементов столбцов меньше единицы, то процесс итерации для данной системы сходится к единственному решению независимо от выбора начального вектора.
следующим образом: если сумма модулей элементов строк или сумма модулей элементов столбцов меньше единицы, то процесс итерации для данной системы сходится к единственному решению независимо от выбора начального вектора. <1 (i=1, 2, …,n) или
<1 (i=1, 2, …,n) или 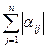 <1 (j=1, 2, …,n)
<1 (j=1, 2, …,n) или
или 


 , где n- число неизвестных данной системы. В нашем примере n =3 и все элементы
, где n- число неизвестных данной системы. В нашем примере n =3 и все элементы  .
.
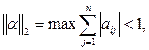

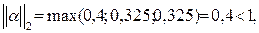
 и
и  - вектор точных значений неизвестных линейной системы, а
- вектор точных значений неизвестных линейной системы, а  есть k - e приближение значений неизвестных, вычисленное методом итерации, то для оценки погрешности
есть k - e приближение значений неизвестных, вычисленное методом итерации, то для оценки погрешности  метода применяется формула
метода применяется формула (1)
(1)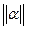 - одна из трех норм матрицы
- одна из трех норм матрицы  - та же норма вектора
- та же норма вектора 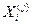 (где j =0, 1, …, k, i =1, 2, …, n) вычисляются точно, в них отсутствуют погрешности округления.
(где j =0, 1, …, k, i =1, 2, …, n) вычисляются точно, в них отсутствуют погрешности округления.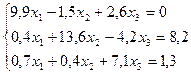
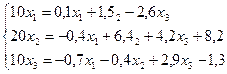


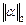 , получаем
, получаем  Следовательно, итерационный процесс для данной системы сходится.
Следовательно, итерационный процесс для данной системы сходится.