
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратичные формы. Кривые второго парядкаСодержание книги
Поиск на нашем сайте
Квадратичной формой двух переменных х и у называется сумма вида f(x,y) = a1x2+2bxy+a2y2. (1) Симметрическая матрица
называется матрицей квадратичной формы f(х,у). Выполним линейную замену переменных:
которое определяется матрицей
Непосредственным вычислением легко проверить, что квадратичная форма (1) перейдет в квадратичную форму от переменных х, у с матрицей TAT'. где Т' получается из Т транспонированием. Квадратичная форма вида l1х12+l2х22 (4) называется канонической, ее матрица является диагональной.
ПОЛОЖИТЕЛЬНЫЕ МАТРИЦЫ Матрица
Теорема. Положительная матрица А всегда имеет положительный характеристический корень l0, который является простым. Все остальные характеристические корни по модулю меньше l0. Собственный столбец, отвечающий l0, может быть выбран положительным. Доказательство. Рассмотрим множество столбцов, определенные соотношением
Очевидно, что нулевой столбец не входит в это множество. Положим для А:
Пусть S(l) – множество всех неотрицательных l, для каждого из которых, найдется неотрицательный столбец Х, такой, что lХ ≤ АХ. Суммируя левые и правые части, получим l ≤ М. Отсюда следует, что S(l) является ограниченным множеством и, кроме того, непустым, поскольку А положительная матрица. Пусть liXi ≤ AXi, i=1, 2,…. Выбираем из l0X0≤AX0, (1) то l Î S(l). Покажем, что в (3.1) выполняется на самом деле равенство. Доказательство проведем от противного. Предположим без потери общности, что
где хi, i = 1, 2, …, n – компоненты вектора Х0. Рассмотрим теперь столбец
Из (3.2) следует, что АY > l0Y. Последнее неравенство противоречит свойству максимальности l0. следовательно, d = 0 и равенство должно иметь место во всех соотношениях (3.2). это означает, что l0 – собственное значение, а Хi – отвечающий ему собственный столбец, который положителен. Покажем теперь, что l0 – наибольшее по модулю собственное значение. Предположим, что существует характеристическое число l матрицы А, такое, что
где Покажем в заключение, что l0 является простым характеристическим числом. Пусть U – вещественный собственный вектор матрицы А, соответствующий l0 и непропорциональный Х0. нетрудно подобрать такое e, чтобы столбец Х0+eU был неотрицательным и имел некоторые компоненты равными нулю, но A(X0+eU)=l0(X0+eU) > 0, и мы приходим к противоречию. Которое доказывает простоту l0. Доказательство теоремы Перрона завершено. Для неотрицательных матриц имеется обобщение теоремы Перрона. Приведем без доказательств формулировку этого результата. Квадратная матрица
Теорема (Фробениуса). Неотрицательная неразложимая матрица А всегда имеет простой положительный характеристический корень R. Все остальные характеристические корни лежат в круге
Упражнения 1. Найти перронов корень и соответствующий ему собственный столбец для матрицы
2. Является ли разложимой матрица
БАЛАНСОВАЯ МОДЕЛЬ
В начале 30-х гг. профессор Гарвардского университета В. Леонтьев предложил линейную модель национальной экономики. Эта модель предполагает, что экономика состоит из некоторого числа взаимодействующих отраслей, каждая из которых производит только один вид продукции и использует только один процесс производства. Например, сельское хозяйство и сталелитейная промышленность могут быть рассмотрены как отрасли. Для продажи своей продукции данная отрасль взаимодействует с другими отраслями и внешним рынком. Итак, пусть хi будет обозначать количество единиц продукции, произведенной i -й скоростью в данном году. Пусть спрос на конечную продукцию этой отрасли равен уi. Пусть хij единиц продукции i-й отрасли потребляет j-я отрасль. Таким образом, если i-я отрасль в точности удовлетворяет спрос внутреннего и внешнего рынка, то
xi = xi1 + xi2 +…+ xin + yi, и мы получаем балансовое уравнение для каждой отрасли i. Важное предположение, сделанное В. Леонтьевым, заключается в линейном законе, т.е. xij = aijxj, где аij – коэффициент пропорциональности, зависит от технологии j-й отрасли. Окончательно xi = аi1x1 +…+ аinxn + yi, i = 1, …, n. (4) Балансовые уравнения (4) могут быть записаны в матричном виде X = AX + Y, где
Количество единиц продукции хi в уравнении (4) может быть заменено их стоимостным и ценовым содержанием. Модель (4), несмотря на свою простоту, может оказаться весьма полезной, для изучения влияния изменения цен в одной отрасли на цены в других отраслях.
Упражнения 1. Для балансовой таблицы «затраты - выпуск»
Найти таблицу технологических коэффициентов и записать балансовую модель в матричном виде. 2. Восстановить недостающие элементы в таблице
Если задана таблица технологических коэффициентов
ПРОДУКТИВНЫЕ МАТРИЦЫ
Запишем матричный вид для балансовой модели X = AX + Y. Известно, что необходимым и достаточным условием существования и единственности элемента Х при любом элементе Y является невырожденность матрицы Е – А, так как (E - A)X = Y. Однако для сохранения экономического смысла решения этого уравнения необходимо дополнительно потребовать, чтобы для любого элемента Y ≥ 0 решение Х было также неотрицательным. Заметим, что не для всякой неотрицательной матрицы А ≥ 0 такое условие выполняется. Например, для матрицы
нет неотрицательных решений для Y ≥ 0. Таким образом, исследование балансовых уравнений сводится к выяснению условий, которым должна удовлетворять неотрицательная матрица А, для того чтобы существовало неотрицательное решение при любом неотрицательном Y. Неотрицательная матрица А > 0 называется продуктивной, если существует хотя бы один такой положительный элемент Х > 0, что (E - A)X > 0. В экономической системе с такой матрицей каждый объект производит конечный продукт. Рассмотрим некоторые свойства продуктивных матриц. Лемма 1. Для продуктивной матрицы А
Доказательство. Пусть матрицы–столбцы Х1 и Х2 связаны соотношением Х1 ≥ Х2, тогда для А ≥ 0 АХ1 ≥ АХ2. С учетом продуктивности А Х > АХ ≥ 0. Для последнего неравенства вытекает существование 0 < l < 1, такого, что lХ > АХ. (5) Умножая (5) слева на матрицу А, получим lАХ > А2Х. (6) Умножая (5) на l получим l2Х > lАХ. (7) Объединяя (6) и (7) получим l2Х > А2Х ≥ 0. Поступая аналогичным образом, можно получить lkХ > АkХ ≥ 0 для любой степени k. Поскольку 0 < l < 1, то элементы матрицы Аk стремятся к нулю при k → ∞, так как Х > 0.
Лемма 2. Если для продуктивной матрицы А существует Х, такой, что Х ≥АХ, (8) то Х ≥ 0. Доказательство.Умножая (8) последовательно k – 1 раз на матрицу А, получим цепочку неравенств Х ≥ АХ ≥ А2Х ≥ АkХ. Рассматривая эту цепочку при k → ∞ и применяя лемму 1, получаем Х ≥ 0.
Лемма 3. Если А – продуктивная матрица, то det(E - A) ≠ 0.
Доказательство. Предположим противное, т.е. det(E - A) = 0, тогда существует Х ≠ 0, удовлетворяющий системе (Е - А) Х = 0, (9) или Х = АХ по лемме 2 Х ≥ 0. (10) Элемент (-Х) также удовлетворяет (3.9), следовательно, по лемме 2.
(-Х) ≥ 0. (11) Объединяя (10) и (11), получаем Х = 0, т.е. система (9) имеет только нулевое решение. Полученное противоречие доказывает лемму.
Теорема 1. Для существования единственного неотрицательного решения Х ≥ 0 для балансовых уравнений (E - A)X = Y при любом неотрицательном Y ≥ 0 необходима и достаточна продуктивность матрицы А.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.71.40 (0.008 с.) |



 (2)
(2) . (3)
. (3) называется положительной (неотрицательной), если
называется положительной (неотрицательной), если  . В первом случае будем писать А >0, во втором А ≥ 0. Рассмотрим весьма важные для экономических приложений свойства положительных матриц.
. В первом случае будем писать А >0, во втором А ≥ 0. Рассмотрим весьма важные для экономических приложений свойства положительных матриц.
 .
. - последовательность чисел l i, сходящаяся к l0, а
- последовательность чисел l i, сходящаяся к l0, а  - последовательность столбцов, таких, что
- последовательность столбцов, таких, что (2)
(2)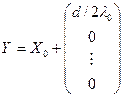 .
. . Пусть Z – соответствующий этому числу собственный столбец, тогда из AZ = lZ следует, что
. Пусть Z – соответствующий этому числу собственный столбец, тогда из AZ = lZ следует, что , (3)
, (3) - это столбец, компоненты которого являются модулями компонент столбца Z. Из неравенства (3.3) и определения l0 следует, что
- это столбец, компоненты которого являются модулями компонент столбца Z. Из неравенства (3.3) и определения l0 следует, что  . Отсюда
. Отсюда  называется разложимой, если множество индексов
называется разложимой, если множество индексов  , которыми занумерованы столбцы и строки, можно разбить на два непустых пересекающихся множества S1 и S2, таких, что аij = 0 для всех iÎS1, jÎS2.
, которыми занумерованы столбцы и строки, можно разбить на два непустых пересекающихся множества S1 и S2, таких, что аij = 0 для всех iÎS1, jÎS2. . Собственный вектор, отвечающий R, может быть выбран положительным.
. Собственный вектор, отвечающий R, может быть выбран положительным. .
. .
. ;
;  ;
;  .
. .
.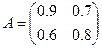
 .
.


