
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Техника решения транспортной задачи вручнуюСодержание книги
Поиск на нашем сайте
(МЕТОД ПОТЕНЦИАЛОВ) Потенциалами выступают определенным образом подобранные числа, с помощью которых можно проверить, является ли допустимый план одновременно и оптимальным. Сумма потенциалов строки и столбца должна быть равна показателю оптимальности cij, т.е.
где
Рассмотрим технику транспортной задачи вручную на конкретном примере, заданном таблицей.
Решение: 1.Составляем первый опорный план методом Северо-Западного угла.
Целевая функция для этого плана F=1880. 2. Определяем потенциалы из первого опорного плана для заполненных клеток.
Значения в выделенных клетках переносятся из условий задачи и равны cij. 3. Заполняем свободные клетки таблицы потенциалов. Рассмотрим более подробно фрагмент:
Показатель Е называется характеристикой свободных переменных. Если Е<0 для всех свободных переменных, то исходный план определяет оптимальное решение. Если Е>0, то можно путем перераспределения поставок улучшить значение функции цели (F). Для этого следует отметить, что перераспределение поставок цепи к этой клетке уменьшает функционал (в расчете на единицу перераспределяемой продукции) на величину характеристики (Е). Вся таблица имеет вид
4. Находим max значение характеристики свободных переменных (E=max). В нашем примере она находится в клетке S2 - D5, и равна 10. 5. Вводим свободную переменную +Q в клетку S2 - D5 (см. первый опорный план). Запомните: Абсолютная величина поставки Q должна быть в точности равна величине возможных ликвидируемых поставок (в нашем случае +Q=20). Баланс по столбцам и строкам не должен нарушаться (в нашем примере из-за введения свободной переменной +Q=20 нарушен баланс по строке S2). Чтобы сохранить баланс в строке S2, вводим в клетку S2 - D3 свободную переменную -Q=20. Этим самым баланс по строке S2 восстановлен, но нарушен баланс по столбцу D3. Восстанавливая его, в клетку S3 - D3 введем переменную +Q=20 и в клетку S3 – D5 – переменную -Q=20. Эта процедура носит название построение цепей. Очевидно, что цепи должны быть замкнуты. 6. Составляем следующий план перевозок: 7.
Для этого плана целевая функция F=1680 (сравн. с первым планом). Приращение функции цели всегда равно Вновь составляем таблицу потенциалов и далее – новый план. Всего для решения рассматриваемой задачи составляется 8 планов перевозок. В итоге 8-й итерации получаем следующее оптимальное решение, для которого целевая функция F=1450→min:
Проверьте себя. Решите транспортную задачу вручную (методом потенциалов). Исходные данные - в следующей таблице: Вариант 13
Примечание Чтобы получить значение функционала в любой момент решения, достаточно найти сумму произведений мощностей на соответствующие им потенциалы строк и произведений спросов на соответствующие потенциалы столбцов. Доказательство: Формула для расчета величины функции цели имеет вид
Так как в пустых клетках величина хij = 0, то формулу можно записать иначе:
но
Вспомнив, что
Мы рассмотрели транспортную задачу и один из алгоритмов ее решения. Известно, что с помощью этого алгоритма можно решать и другие производственные задачи, а именно задачу о загрузке оборудования, задачу о назначении рабочих на работу, задачу о составлении плана-графика деталей в производство и другие. Но существует целый ряд производственных задач, которые нельзя свести к транспортной задаче.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.248.17 (0.01 с.) |


 - потенциал строки;
- потенциал строки;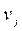 - потенциал столбца;
- потенциал столбца; - критерий оптимальности (равный показателю cij из условия задачи для вошедших в опорный план клеток).
- критерий оптимальности (равный показателю cij из условия задачи для вошедших в опорный план клеток).

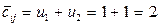
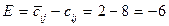

 .
. .
. .
. . Отсюда
. Отсюда .
. и
и  , получим
, получим .
.


