
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симплексный метод решения задач линейного программированияСодержание книги
Поиск на нашем сайте
24.1 ОБЩАЯ ФОРМУЛИРОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задачи линейного программирования могут быть сведены к канонической форме. Введем обозначения: xj – искомые неизвестные, переменные величины (j = 1,…., n); aij – коэффициенты при неизвестных в уравнениях и неравенствах исходных ограничений; bi - величина ограничения в соответствующем уравнении или неравенстве; сj – коэффициенты, с которыми неизвестные хj входят в целевую функцию.
Формулировка задачи на максимум при n неизвестных дает функцию цели вида F = c1x1 + c2x2 + ….+ cjxj +….+ cnxn ® max. Если мы имеем дело с канонической формой, то исходные ограничения задаются равенствами (в количестве m), т.е.
Выделяются требования неотрицательности неизвестных хj, т.е. хj > 0. Если мы имеем дело с производственными задачами, то ограничения в них обычно принимают форму неравенств (хотя бывают и равенства). Функция цели формулируется в них как на максимум, так и на минимум. Тогда в общем виде и не в канонической форме задача линейного программирования записывается так: F=c1x1+c2x2+...+cjxj+….+cnxn→max(min). От общей формулировки задачи линейного программирования можно перейти к канонической. 1. Если в ограничениях не все значения bi положительны, т.е. имеются некоторые bi < 0, то необходимо все члены соответствующего уравнения (неравенства) умножить на (-1). 2. Чтобы преобразовать ограничение, записанное в форме неравенства, его превращают в уравнение. Для этого в него добавляется фиктивное неизвестное. При этом стараются в каждое неравенство ограничения ввести собственную фиктивную переменную, знак которой зависит от вида неравенства. Так, в неравенстве вида «<» фиктивные переменные вводятся со знаком плюс, а в неравенства вида «>» - со знаком минус. В результате, после преобразование любой системы неравенств в систему симплексных уравнений, количество неизвестных в последней всегда будет больше количество уравнений. Кроме того, образуется единичная подматрица. С помощью этой подматрицы имеется возможность получения в исходной симплексной таблице допустимого решения и проверки его на оптимальность. Примечание Анализ системы (определение ранга матрицы) при больших ее размерах может оказаться очень трудоемким. Поэтому целесообразно сразу применять симплексную процедуру, а не отыскивать линейно независимые уравнения.
24.2 ЗАПОЛНЕНИЕ СИМПЛЕКСНОЙ ТАБЛИЦЫ ПО СТРОКАМ
1. В первой верхней строке симплексной таблицы записываются показатели критерия оптимальности, т.е. коэффициенты при неизвестных в уравнении целевой функции F. 2. Вторая строка симплексной таблицы называется шапкой матрицы. В ней указываются номера всех неизвестных (основных и фиктивных), входящих в данную систему.
Симплексная таблица
3. Далее идут строки, основная часть которых занята коэффициентами при неизвестных в уравнениях исходных условий. Этих строк должно быть в матрице столько, сколько в данной задаче ограничений, или столько, сколько дополнительных неизвестных. 4. Последняя строка носит название целевой строки и заполняется двойственными оценками.
24.3 ЗАПОЛНЕНИЕ СИМПЛЕКСНОЙ ТАБЛИЦЫ ПО СТОЛЦАМ
1. Первый столбец – коэффициенты сj. Он, как и первая строка, отводится для показателей критерия оптимальности. Отличие между первой строкой и первым столбцом состоит в следующем: a) Первая строка, в отличие от столбца, сохраняется лишь в первой симплексной таблице. Начиная со второй итерации верхняя строка перестает быть обязательной. b) В первой строке указываются все без исключения (и основные, и дополнительные) показатели критерия оптимальности, т.е. все коэффициенты, с которыми неизвестные входят в целевую функцию. В первый же столбец входит только часть коэффициентов при неизвестных в целевой функции, т.к. число строк в матрице равно числу дополнительных неизвестных. Эта часть состоит из показателей, номера которых указаны во втором столбце (рk).
2. Второй столбец – рk (индеек k – номер итерации). В этом столбце указываются номера неизвестных, входящих в базисное решение. Эти номера используют для нумерации соответствующих строк матрицы. В первой симплексной таблице в столбце р0 указываются номера всех дополнительных переменных. 3. Третий столбец – х0. В первой симплексной таблице он заполняется свободными членами уравнений из системы ограничений. В процессе итеративного расчета эти показатели преобразуются в искомое решение. Поэтому данный столбец носит название итогового столбца. 4. Значение целевой функции Fk. На пересечении итогового столбца в целевой строке указывается значение функционала Fk, соответствующее данному этапу решения, данной итерации k. 5. Столбцы «основания матрицы». Обычно сначала располагаются столбцы для основных неизвестных, а вслед за ними – для дополнительных неизвестных. В этих столбцах в первой симплексной таблице приводятся коэффициенты при неизвестных из уравнений исходных условий. 6. Последующие три столбца таблицы (å, a, b) имеют вспомогательное значения. Без этих столбцов можно обойтись, но они существенно облегчают проведение расчетов. Более подробно содержание этих столбцов будет рассматриваться ниже.
Пример Рассмотрим симплексную задачу, записанную в общем виде: F = 15x1 + 20x2 +5x3 ® max.
Приведем задачу к канонической форме. Для этого в каждое из неравенств системы введем по одному неизвестному (дополнительному) – х4, х5. х6. Тогда F = 15x1 + 20x2 +5x3 ® max.
Заполним первую симплексную таблицу.
Мы заполним все клетки, исходя из условий задачи. Чтобы заполнить клетку F0 в первой таблице, необходимо просуммировать произведения элементов столбца х0 на элементы столбца с0, т.е. F0 = 600∙0 + 520∙0 +600∙0 =0. Чтобы заполнить целевую строку в первой таблице, необходимо соответствующее значение сj вычесть из суммы произведений элементов столбца хj на элементы столбца с0. Для столбца х1 величина двойственной оценки будет определяться (0∙80+0∙15+0∙5) – 15=-15; Для х2: (0 35+0 60+0 5) – 20=-20; х3: (0 10+0 0+0 90) – 5=-5 и т.д. В итоге первая симплексная таблица будет выглядеть так: Таблица 1
Решение: Прежде чем приступать к решению, необходимо проверить, является ли предложенный в таблице план (решение) оптимальным. Определение Решение считается оптимальным, если все значения чисел в целевой строке положительны. Если полученное решение не является оптимальным, то его можно улучшить. Для этого нужно: 1. Выбрать максимальное по абсолютной величине отрицательное значение числа в целевой строке. В нашем примере таким числом будет (-20), находящееся в столбце «х2». Именно это значение задает ключевой столбец.
Обратите внимание: Ключевой столбец показывает, какое из хj войдет в новое решение задачи. В нашем случае - неизвестное х2. Обратите внимания: Чтобы включить в новое решение неизвестное хj, улучшающее это решение, необходимо вывести из базисного решения одно из хj, входящее в него. 2. Выбрать минимальное значение частного от деления элементов столбца х0 на элементы ключевого столбца. Результаты этих расчетов заносятся в столбец «a» симплексной таблицы. В нашем примере эти отношения равны: 600/35=17,14; 520/60=8,67; 600/5=120. Минимальное значение соответствует х5 и равно 8,67. Это отношение задает ключевую строку. 3. Выбрать элемент, находящийся на пересечении ключевого столбца и ключевой строки, который называется ключевым элементом. В нашем примере ключевой элемент равен 60 и находится на пересечении столбца х2 и строки х5. Обратите внимание: Ключевым не может быть столбец, все элементы которого оказались отрицательными или нулевыми. 4. Просуммировать элементы матрицы по строкам (начиная от столбца х0 и кончая столбцом х6). Полученные суммы записываются в столбец «å». 5. Преобразовать ключевую строку. Для этого a) Каждый элемент ключевой строки делится на ключевой элемент, начиная с элемента столбца «х0»; Фрагмент
b) В столбце р1 записывается х2 вместо х5; c) В столбце сj записывается значение критерия оптимальности при х2, т.е. 20. 6. Все остальные элементы симплексной таблицы пересчитывают, подчиняясь основному правилу. Это правило получило название правила диагонали или правила треугольника.
*
Если мы хотим в нашем примере пересчитать первый элемент столбца х0, который равен 600, то необходимо произвести следующие вычисления:
При пересчете величины функции цели получаем:
Аналогичным образом поступаем со всеми другими элементами таблицы. В итоге получаем новую симплексную таблицу. Таблица 2.
Как видно из табл. 2, оптимальное решение не получено, т.е. необходимо продолжить решение, используя все рассмотренные правила преобразования симплексных таблиц.
Примечание 1. Столбец «å» используется для проверки хода решения по строкам. Сумма новых значений элементов строки должна равняться величине элемента этой строки и столбца «å», преобразованного по правилу диагонали. Примечание 2. Величина функции цели должна равняться сумме произведений элементов столбца сj на элементы столбца х0. Самостоятельно дорешайте эту задачу. В результате должно получиться: F=236.7; x1=3.31; x2=7.8; x3=6.05. Примечание 3. В столбце «b» записываются частные от деления элемента в ключевом столбце и строке i на ключевой элемент. Примечание 4. В следующей таблице начинайте вычисления с помощью правила диагонали с целевой строки. Если все оценки положительны, то найдено оптимальное решение и остается заполнить столбец х0. В этом случае основание матрицы пересчитывать не обязательно.
24.4 ДВОЙСТВЕННЫЕ ЗАДАЧИ, ОЦЕНКИ, ПРОБЛЕМЫ. ДВОЙСТВЕННАЯ ФОРМУЛИРОВКА ЗАДАЧИ О ЗАГРУЗКЕ ОБОРУДОВАНИЯ
Прямая постановка задачи: Есть несколько станков: А1, А2, …, Аm. Задано максимальное время использования каждого из них: b1, b2, …, bm. На станках можно выпустить детали нескольких видов: В1, В2, …, Вn. Известна величина прибыли, получаемой при продаже каждого изделия: с1, с2, …, сj, …, cn. Известны показатели, характеризующие затраты времени станка Аi на выпуск одной детали Вj – матрица чисел (aij). Требуется установить, сколько и каких деталей выпускать, т.е. найти значение неизвестных х1, х2, …, хn. Математически задача формулируется так: F = c1x1 + c2x2 + ….+ cjxj +….+ cnxn ® max.
Двойственная постановка этой задачи естественна и ее легко объяснить. Допустим, что мы хотим арендовать станки и надо решить, по каким ценам рассчитываться за каждый станко-час. Естественно, что мы будем стараться уплатить как можно меньше, но при этом должны учитывать, что при слишком низких ценах нам могут отказать в аренде станков. Чтобы этого не случилось, необходимо установить цены, выгодные арендатору. То есть цены должны быть такими, чтобы при умножении на них часов работы станков, необходимых для выпуска детали Вj, получилась сумма не меньше, чем величина прибыли при продаже этой детали. Цель в том, чтобы минимизировать общую сумму затрат на оплату аренды всех станков. Цены, отвечающие заданным условиям, называются оптимальными. Обозначим величины цен через Сумма произведений возможного времени работы каждого станка на соответствующую цену должна быть минимальна:
Чтобы ввести ограничения, изображаются суммы произведений часов работы каждого станка для производства одной детали на соответствующие цены. Каждая такая сумма должна быть не меньше размера прибыли от продажи одной детали. Для выпуска одной детали расходуется а11 часов работы станка А1, а21 часов работы станка А2 и т.д. Значит за время, достаточное для ее выпуска, плата за аренду должна составить
Общая сумма должна быть не меньше прибыли при продаже им оной детали В1. Тогда система ограничений имеет вид
Решение двойственной задачи дает тот же результат, что и решение прямой задачи. В каждой паре сопряженных задач рассматриваются одни и те же исходные показатели, но в разных ограничениях. Те показатели, которые в одной из пары сопряженных задач характеризуют размер ограничений (свободные члены уравнений), являются в двойственной задаче коэффициентами при неизвестных в уравнении целевой функции, и наоборот, коэффициенты, с которыми входит в целевую функцию неизвестные одной задачи, характеризует размер ограничения в другой. Матрица коэффициентов при неизвестных входит в обе задачи, но в одной из них она трансформирована по отношению к другой. Знаки неравенств в одной задаче заменяются на противоположные в другой. Решение получается одинаковым в обеих задачах.
Ответы к вариантам: Вар.1 S1-D1/40/, S2-D1/10/, S2-D2/10/, S2-D3/30/, S3-D3/40/, S4-D3/30/, S4-D4/20/. Вар.2 S1-D1/90/, S2-D2/10/, S2-D2/50/, S3-D2/10/, S3-D3/80/, S3-D1/10/, S4-D4/20/. Вар.3 S1-D1/20/, S2-D1/30/, S2-D2/40/, S3-D2/20/, S3-D3/10/,S4-D3/40/, S4-D4/40/. Вар.4 S1-D1/40/, S2-D1/30/, S2-D2/30/, S3-D2/30/, S3-D3/10/, S4-D3/60/, S4-D4/20/. Вар.5 S4-D1/30/, S1-D1/20/, S1-D2/40/, S2-D2/30/, S2-D2/30/,S3-D3/10/, S3-D4/40/. Вар.6 S2-D1/60/, S1-D1/10/, S1-D2/30/, S4-D2/30/, S3-D3/20/, S3-D4/10/, S4-D4/60/. Вар.7 S2-D1/20/, S1-D2/50/, S4-D2/50/, S2-D3/10/, S3-D4/10/, S4-D4/30/, S2-D4/10/. Вар.8 S4-D1/20/, S2-D1/10/, S3-D1/70/, S3-D2/60/, S1-D3/80/, S3-D4/20/, S1-D4/10/. Вар.9 S2-D1/10/, S4-D1/40/, S4-D3/10/, S3-D4/20/, S1-D3/80/, S3-D2/10/, S3-D3/10/. Вар.10 S4-D1/20/, S2-D1/10/, S3-D2/60/, S1-D1/70/, S3-D3/80/, S1-D4/20/, S3-D4/10/. Вар.11 S1-D3/50/, S2-D4/40/, S1-D2/10/, S3-D1/30/, S3-D2/30/, S4-D2/20/, S2-D2/10/. Вар.12 S1 –D2/50/, S2-D1/40/, S2-D3/30/, S3-D3/10/, S3-D4/10/, S4-D4/50/, S1-D4/10/. Вар.13 ЦФ=940, число итереций=5.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.18.220 (0.015 с.) |


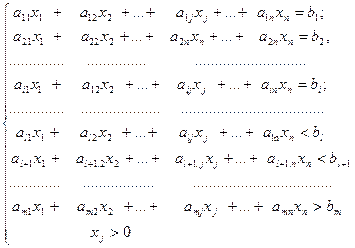




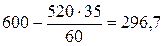 .
.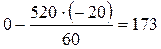 .
.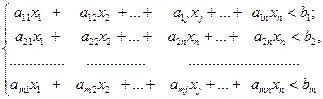
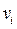 , т.е.
, т.е.  - цена за 1 час аренды станка А1,
- цена за 1 час аренды станка А1,  - цена за 1 час аренды станка А2 и т.д.
- цена за 1 час аренды станка А2 и т.д.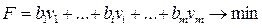 .
.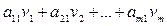 .
.



