
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретация задач линейного программированияСодержание книги
Поиск на нашем сайте
Если в задаче количество неизвестных n больше числа независимых уравнений m на 2, т.е. n – m = 2, то такой задаче можно дать геометрическую интерпретацию. Для этого выбираем свободные переменные, например х1 и х2. Остальные переменные будут являться базисными. Их можно выразить через свободные переменные следующим образом:
Значения свободных переменных х1 и х2 откладываются по осям Ох1 и Ох2. Эти переменные не могут быть отрицательными, поэтому допустимые значения этих свободных переменных могут лежать только выше оси Ох1 и правее оси Ох2 (см. рис.1).
Рис. 1. Графическое представление свободных переменных в задачах линейного программирования
Базисные переменные также должны быть неотрицательными, т.е.
Пусть х3 = 0, т.е.
Это уравнение прямой, которую можно построить в системе координат х1Ох2. Прямая х3 = 0 проходит таким образом, что по одну сторону от этой прямой лежат точки, соответствующие х3 > 0, а по другую – соответствующие х3 > 0. Поэтому х3 = 0 делит всю область переменных х3 на две полуплоскости – допустимых и запрещенных значений (см. рис.1). Таким же образом строятся и все остальные ограничивающие прямые: х4 = 0, х5 = 0, … хn = 0. Штриховкой отмечается допустимая область. Каждая прямая соответствует обращению в 0 одной из переменных. В точках пересечения в 0 будут обращаться две переменные. Число (n - m) определяет число свободных переменных. Их обращение в 0 соответствует базисному решению. Все переменные в совокупности ограничивают область допустимых решений (ОДР), которая представляет собой выпуклый многоугольник (рис.2).
Рис. 2. Выделение области допустимых решений
Цель задачи заключается в нахождении оптимального решения, которое обращает линейную функцию цели при n – m =
где Допустим, что
Тогда получаем уравнение прямой на плоскости х1Ох2. Угловой коэффициент этой прямой равен При изменении величины Q угловой коэффициент прямой не изменится. Изменяется только начальная ордината, т.е. прямая
Рис. 3. Образование линий равного уровня целевой функции
Рис. 4. Направления убывания Q линий равного уровня целевой функции при различных коэффициентах: а - Функция цели L достигает максимального значения, когда прямая будет проходить через крайнюю точку области допустимых решений, наиболее удаленную от начала координат. Координата этой точки (х1, х2) определяет оптимальное решение задачи линейного программирования. Для примера найдем максимальное значение функции цели F= 4x1 + 3x2 при ограничениях
Рис. 5. Область допустимых значений для х1>5 и х2>15
Область допустимых значений для х1 будет располагаться справа от прямой х1=5, а для х2 – сверху от прямой х2 = 15. Аналогичным образом поступим с тремя оставшимися ограничениями. Запишем их сначала как равенства. Каждое из этих равенств является уравнением прямой, которое можно изобразить графически. Найдем оптимальное решение задачи. Пусть F= 4x1 + 3x2 = Q.
Рис. 6. Направление движения прямой F при увеличения значений Q
Максимальное значение целевой функции приходится на одно из крайних положений прямой F в пределах области допустимых значений. Оптимальное решение считается найденным, если точка пересечения прямой F с наиболее удаленной (по ходу F) вершиной выпуклого многогранника ABCDE. В нашем примере такой точкой будет точка D(30, 20) (рис. 7).
Рис. 7. Оптимальное решение задачи
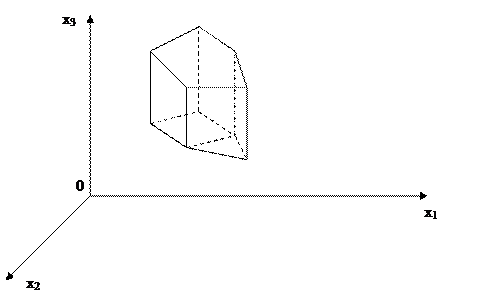
Подставляя координаты этой точки в уравнение целевой функции, получим решение данной задачи: F= 4x1 + 3x2 = 4∙30+3∙20=180. Если увеличить число переменных таким образом, что n – m = 3, то для геометрической интерпретации необходимо пространственное построение объемной области допустимых решений. Область допустимых решений (если она существует) представляет собой выпуклый многоугольник (рис. 8).
Рис. 8. Графическое представление задачи линейного программирования в случае n – m=3.
Вместо прямой постоянного уровня целевой функции для n – m = 2, в случае n – m = 3 возникает поверхность постоянного уровня целевой функции. Ее уравнение
Если количество свободных переменных х1, х2, х3 больше 3, то решение задачи линейного программирования можно осуществлять геометрическим построением выпуклого многогранника допустимых решений в неотрицательном октанте n-мерного функционального пространства.
Проверьте себя. Найдите геометрическим способом оптимальное решение задачи F=20x1+35x2 ® min при ограничениях
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.114.163 (0.007 с.) |

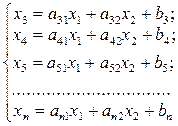


 .
.
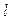 в min (max). Этой задаче можно дать геометрическую интерпретацию. Для этого подставим в уравнение целевой функции значения базисных переменных. Получим
в min (max). Этой задаче можно дать геометрическую интерпретацию. Для этого подставим в уравнение целевой функции значения базисных переменных. Получим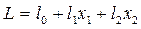 ,
,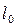 - свободный член (его в первоначальном виде не было, но он может появиться при переходе к переменным х1 и х2).
- свободный член (его в первоначальном виде не было, но он может появиться при переходе к переменным х1 и х2).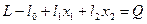 .
.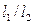 . На оси ординат эта прямая отсекает отрезок, равный
. На оси ординат эта прямая отсекает отрезок, равный  .
.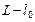 перемещается параллельно самой себе, образуя линии равного уровня целевой функции.
перемещается параллельно самой себе, образуя линии равного уровня целевой функции. Если
Если  , то поученная прямая проходит через начало координат (рис. 3).
, то поученная прямая проходит через начало координат (рис. 3). Направление, в котором должна двигаться основная прямая, чтобы величина Q убывала, зависит от знаков коэффициентов
Направление, в котором должна двигаться основная прямая, чтобы величина Q убывала, зависит от знаков коэффициентов 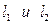 . Если оба коэффициента положительны, то прямая будет двигаться вниз и влево (рис. 4а) и т. д. Направление движения прямой при различных коэффициентах
. Если оба коэффициента положительны, то прямая будет двигаться вниз и влево (рис. 4а) и т. д. Направление движения прямой при различных коэффициентах 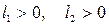 ; б -
; б - 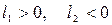 ; в -
; в - 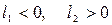 ; г -
; г - 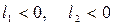 .
.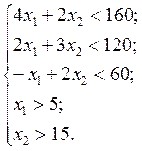
 Решим эту задачу графически. Сначала построим область допустимых значений для двух ограничений: х1>5 и x2>15 (рис. 5).
Решим эту задачу графически. Сначала построим область допустимых значений для двух ограничений: х1>5 и x2>15 (рис. 5). Если Q=0, то прямая F проходят через начало координат. С увеличением значения Q прямая будет перемещаться в направления, указанном на рис. 6.
Если Q=0, то прямая F проходят через начало координат. С увеличением значения Q прямая будет перемещаться в направления, указанном на рис. 6.
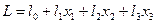 .
.



