Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка транспортной задачиСодержание книги
Поиск на нашем сайте
Предположим, имеется несколько предприятий-производителей. Они вывозят готовую продукцию на заводы-потребители. Перевозимая продукция должна быть однотонной и взаимозаменяемой. Поставщики находятся от потребителей на различном расстоянии. Количество продукции в цехах-изготовителях будем именовать мощностью. Потребность цехов-потребителей в заданной продукции будем называть спросом.
20.1 МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ТРАНСПОРТНОЙ ЗАДАЧИ.
Пусть заданы векторы Si, Dj и cij, где Si – мощность i-го цеха-изготовителя (i=1,…,m); Dj – спрос j-го цеха-потребителя (j=1,…, n); cij – расстояние между каждым i-м поставщиком и j-м потребителем; m – количество поставщиков; n – количество потребителей. Необходимо найти неизвестные показатели хij – количество продукции, перевозимой от поставщиков к потребителю (обратите внимание, что многие показатели хij могут принимать нулевые значения). Запомните: Элементы матрицы cij называются критериями оптимальности. Совокупность всех элементов матрицы хij называются планом перевозки.
Проверьте себя: Правильны ли следующие утверждения? 1. Векторы S и D называют критериями оптимальности. 2. Элементы cij называют планом перевозки. 3. Элементы хij называют планом перевозки. 4. Элементы cij называют критериями оптимальности. 5. Показатели хij > 0. 6. Показатели хij < 0. 7. Показатели хij > 0. 8. Неизвестными являются показатели хij. 9. Неизвестными являются показатели сij. 10. Неизвестными являются показатели Si и Dj. Рассмотрим условия задачи с помощью таблицы.
1. Каждый поставщик должен отдать потребителям столько продукции, сколько у него есть. Это значит, что сумма поставок по строке должна быть равна мощности этой строки, т.е.
Таких соотношений столько, сколько строк в таблице. 2. Каждый потребитель должен получить столько продукции, сколько ему требуется. Это значит, что сумма поставок по столбцу должна быть равна спросу этого столбца, т.е.
Таких соотношений столько, сколько столбцов в таблице. 3. Поскольку полная сумма не зависит от того, как производилось суммирование (по строкам или по столбцам), то сумма мощностей производителя должна быть равна суммарному спросу всех потребителей, т.е.
4. Требуется составить такой план перевозок, при котором грузооборот будет минимальным
Этот план называется оптимальным. 5. Показатели мощностей и спросов должны принимать неотрицательные значения, т.е. Si > 0 и dj > 0. 6. Отрицательных поставок быть не должно, т.е. хij > 0.
7. К показателям cij с математической точки зрения не предъявляется требование неотрицательности. Это вытекает из здравого смысла, т.е. cij > 0. Проверьте себя: Какие утверждения являются неправильными? 1. Потребитель получает всю продукцию первого же поставщика. 2. Соотношений 3. Соотношений 4. Функция цели формулируется следующим образом:
5. Показатели Si и dj должны быть неотрицательными. 6. Поставки хij должны быть неотрицательными.
Запомните: Количество неизвестных в задаче равно m×n. Количество уравнений равно m + n. Одно (любое) уравнение линейно зависимо от остальных. Количество линейно независимых уравнений равно m + n - 1.
20.2 БАЗИСНОЕ РАСПРЕДЕЛЕНИЕ В ТРАНСПОРТНОЙ ЗАДАЧЕ
Чтобы получить оптимальный план, необходимо в первую очередь получить базисное распределение плана (перевозок). Базисный план должен быть как можно более приближенным к оптимальному. Существует несколько способов его составления. СПОСОБ СЕВЕРО-ЗАПОДНОГО УГЛА Чтобы воспользоваться этим способом, необходимо заполнить таблицу, начиная от левого верхнего угла и кончая нижним правым углом. Посмотрим, как это делается, на примере. Условия задачи представлены в таблице.
Начинаем заполнять таблицу с клетки S1 - D1 (20).
Затем последовательность заполнения выглядит следующим образом: S1 - D1 (25); S2 – D2 (5); S3 – D2 (40); S4 – D2 (10); S4 – D2 (10); S4 – D3 (40); S5 – D3 (11); S5 – D4 (49). Проверьте себя. Перепишите в тетрадь условия задачи и составьте первый опорный план табличным способом. Вариант 1
Вариант 2
Вариант3
Вариант 4
СПОСОБ НАИМЕНЬШЕГО ЭЛЕМЕНТА В СТОЛБЦЕ (СТРОКЕ) Чтобы воспользоваться этим способом, необходимо поочередно в столбцах (строках) матрицы заполнить клетки, соответствующие минимальным значениям cij. Если при записи спрос по столбцу (или мощность по строке) удовлетворен не полностью, ищем следующий по величине элемент в данном столбце (строке). Такие операции проводятся до полного удовлетворения спроса. После этого переходят к следующему столбцу (строке).
Обратите внимание: Если в столбце (строке) два или несколько одинаковых по величине показателей ct j, то для составления плана перевозки может быть взят любой из них. В качестве примера заполним (построчно) методом наименьшего элемента таблицу с предыдущего примера. Заполнение начинаем с клетки S5- D1 (45).
Затем последовательность заполнения выглядит следующим образом: S1 – D2 (20); S2 – D2 (30); S5 – D2 (5); S5 – D3 (10); S3-D3 (40); S4 – D3 (1); S4 – D4 (49).
Проверь себя. Перепишите в тетрадь условия задачи и составьте опорный план способом наименьшего элемента в столбце (строке). Вариант 5
Вариант 6
Вариант 7
Вариант 8
СПОСОБ НАИМЕНЬШЕГО ЭЛЕМЕНТА В МАТРИЦЕ Чтобы воспользоваться этим способом, необходимо поочередно во всей матрице заполнять клетки, соответствующие минимальным значениям ctj. Для этого находят наименьший элемент ct j и матрице приносят в эту клетку первую поставку xtj, затем наименьший из оставшихся и т.д. Вновь рассмотрим таблицу с предыдущего примера. Начинаем заполнять ее способом наименьшего элемента в матрице с клетки S1 – D2 (20)
Затем последовательность заполнения клеток выглядит следующим образом: S2 – D3 (30); S5 – D3 (21); S5 – D1 (39); S4 – D1 (6); S3 – D4 (40); S4 – D4 (9); S4 – D2 (35).
Проверь себя. Перепишите в тетрадь условия задачи и составьте первый опорный план способом наименьшего элемента в матрице. Вариант 9
Вариант 10
Вариант 11
Вариант 12
Запомните: При составлении первого спорного плана возможен случай вырождения. Он возникает, когда все условия выполнены, а число элементов xtj будет меньше числа m+n-1. Чтобы избежать вырождения, необходимо внести фиктивную (нулевую) поставку. В качестве примера рассмотрим опорный план, составленный методом Северо-Западного угла. Количество заполненных клеток должно быть равно m+n-1=4+4-1=7
В нашем примере его число равно 6, т.е. мы имеем дело со случаем вырождения. Чтобы устранить его, вводим фиктивную (нулевую) поставку в любую из свободных клеток, например в клетку S2 – D4. Тогда наш опорный план будет иметь вид
Примечание Если опорный план составлен методом «наименьшего элемента в строке (столбце)» или «наименьшего элемента в матрице», то фиктивную поставку следует вводить, в пустую клетку, которая содержит очередное минимальное значение критерия. С помощью такой простой процедуры мы избавимся от случая вырождения. Но это лишь одна проблема. Другая же заключается в том, что на практике условие транспортной задачи, по которому сумма мощностей должна равняться суммарному спросу всех потребителей, не выполняется, т.е.
В этом случае задача называется открытой транспортной задачей. Чтобы перейти к закрытой транспортной задаче, достаточно ввести в условия задачи фиктивного поставщика или фиктивного потребителя. Рассмотрим задачу по таблице.
Из условия задачи видно, что суммарная мощность меньше суммарного спроса на 40 (160-120=40),т.е. мы имеем дело с открытой транспортной задачей. Чтобы ее закрыть, введем в условия задачи фиктивного поставщика S5. Его мощность будет равна 40 т.к. в действительности такого поставщика не существует, то мы в праве считать, что расстояние до него от каждого потребителя будет равно 0. После такого преобразования условия задачи будут выглядеть следующим образом:
Проверь себя. 1. Можно ли избежать вырождения? 2. Количество заполненных клеток должно быть равно m+n? 3. Количество заполненных клеток должно быть равно m+n-1? 4. Что делать, если суммарный спрос превышает суммарные запасы?
Итак, мы получили первый опорный план. Теперь мы должны проверить, является ли он оптимальным, т.е. можно ли его улучшить, уменьшая целевую функцию
Для этой цели воспользуемся методом потенциалов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |





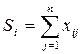 должно быть столько, сколько столбцов в матрице задачи.
должно быть столько, сколько столбцов в матрице задачи. должно быть столько, сколько столбцов в матрице задачи.
должно быть столько, сколько столбцов в матрице задачи.
 20
20