
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательство необходимости.Содержание книги
Поиск на нашем сайте
Пусть существует Х ≥ 0 при любом Y ≥ 0, среди которых выберем Y > 0, т.е. (E - A)X = Y > 0. (12) Покажем, что Х>0. Действительно, из (12) вытекает Х – АХ > 0 или Х > АХ, Так как А ≥ 0 и Х ≥ 0, то Х > АХ ≥ 0 и, следовательно, Х>0. существование элемента Х>0 для неравенства (E - A)X > 0 доказывает продуктивность матрицы А. Доказательство достаточности. Балансовое уравнение (E - A)X = Y с продуктивной матрицей А по лемме 3 имеет единственное решение при любом Y. Если Y ≥ 0, то Х ≥ АХ. В силу леммы 2 Х ≥ 0, и теорема доказана полностью. При расчете производительной программы Х необходимо заранее знать, является ли матрица технологических коэффициентов продуктивной. Рассмотрим критерии продуктивности.
Теорема 2. Матрица А ≥ 0 продуктивна тогда и только тогда, когда матрица S=(E - A)-1 существует и неотрицательна. Доказательство необходимости. Пусть А – продуктивная матрица. Запишем, согласно определению обратной матрицы, (Е - А)S = Е. (13) Представим матрицу S и E в блочно – столбцовом виде:
Тогда матричное уравнение (13) эквивалентно n уравнениям (Е - А)Sj = Ej, j = 1, …, n. (14) Так как Ej неотрицательна, то, по теореме 3.6, Si ≥ 0. Доказательство достаточности. Пусть S существует и неотрицательна. Покажем, что существует элемент Х>0, для которого Х > АХ. Рассмотрим матрицу-столбец U, элементами которой являются единицы. Пусть X = SU. (15) Поскольку S не может иметь строк, состоящих из одних нулей, то Х>0. Умножая (15) слева на (Е - А), получаем (Е - А)Х = U > 0, что доказывает продуктивность матрицы А.
Упражнения 1. Используя соотношение (14), дайте экономическое толкование столбцам матрицы S. 2. Являются ли следующие матрицы продуктивными: а) 3. Может ли продуктивная матрица иметь характеристический корень, равный 1. 4. Может ли продуктивная матрица быть диагональной; ортогональной.
НОРМА МАТРИЦЫ
Рассмотрим матричную характеристику, которую можно грубо трактовать как «длину» матрицы. Определение. Неотрицательное число 1.
2. 3. 4. 5. Свойства 1-5 должны выполняться для любых матриц А, В и любого скаляра l. При этом матрицы А и В имеют размеры, необходимые для сложения и умножения.
Определение допускает различные способы вычисления нормы матрицы. В то же время это понятие должно обслуживать задачи, связанные с собственными значениями и системами уравнений. Действительно, переходя к нормам в определении собственного столбца АХ = lХ, получим:
последнее неравенство будет иметь практическое значение, если
Отсюда
Выражение
будет всегда меньше любой нормы матрицы А. Непосредственной проверкой можно убедиться, что это выражение удовлетворяет свойствам 1-5, т.е.
Ясно, что это выражение зависит от способа вычисления Х = (х1х2…хn)Т
Это формула задает семейство р-норм
Подсчитаем 1-норму матрицы, обозначив
Знак равенства может достигаться для матрицы, у которой все компоненты ненулевые за исключением k-го, который равен 1, и
Упражнения 1. Найти 2. Найти 1 – норму матриц:
а) 3. Найти ∞ - норму для упражнения 2. 4. Доказать: а) б)
ИТЕРАЦИОННЫЙ МЕТОД Методы решения линейных алгебраических уравнений, такие, как правило Крамера или метод исключения Гаусса, могут быть применены для расчета производственной программы Х или элементов обратной матрицы (Е - А)-1. Однако корректное применение этих методов требует вычисления определителей. Для матриц небольших размеров применение этих методов оправдано. Для матриц больших размеров более оправдано применение итерационных методов и ЭВМ. Рассмотрим балансовое уравнение в матричной форме X = AX + Y (17) и последовательность матриц
Воспользуемся понятием матричной нормы для анализа поведения последовательности
Из уравнения (17) Y = X – AX. Тогда
Переходя к нормам, получим
Если
Чтобы установить скорость стремления
x1 £ qx0
x2 £ qx1 … xk+1 £ qxk … Отсюда xk+1 £ qk+1x0 и скорость стремления xk к нулю не хуже, чем скорость стремления к нулю общего члена геометрической прогрессии со знаменателем q.
Упражнения 1. Написать итерационный метод для решения системы линейных алгебраических уравнений АХ = В. 2. Доказать сходимость (18) если А – продуктивная матрица.
ВОЗМУЩЕНИЕ РЕШЕНИЙ
В этом параграфе рассмотрим влияние возмущений в матрице и правой части на решение уравнений вида AX = Y. (19) Теорема. Справедливо неравенство
Доказательство. Неравенство E+A=E+TJT-1=T(E+J)T-1. Отсюда Справедливы равенства Е=(Е+А)-1(Е+А)=(Е+А)-1+(Е+А)-1А. Так как
Отсюда
Предположим, что для квадратной матрицы А существует обратная матрица А-1, следовательно, решение Х уравнения (19) единственно. Пусть вместо точных входных данных известны возмущенные входные данные Аh. Yd:
Итак, пусть А переходит а Аh, Y переходит вYd. Тогда Х перейдет в Хy, которое удовлетворяет уравнению АhXy=Yd. Запишем обозначения для возмущений H=Ah-A, D=Yd-Y, y=Xy-X. Возмущенное решение удовлетворяет уравнению (A+H)(X+y)=Y+D. Вычитая (3.19) из (3.20), получим (A+H)y=D-НХ. Предположим, что
Выразим y=(А-Н)-1(D-НХ)=(Е-А-1Н)-1А-1(D-НХ). Переходя к нормам, получим
Теорема 3.8 дает
Из (19) следуют неравенства
Следует отметить решающую роль в этой оценке числа
Системы линейных уравнений, для которых это число велико, называются плохо обусловленными.
Упражнения 1. Доказать, что если матрица А невырождена и 2. Показать, что число обусловленности cond(A) не меняется при умножении матрицы А на ненулевое число. 3. Доказать неравенство
4. Оценить возможное возмущение решений систем:
при изменении компонент правой части на 0.01.
ДЕМОГРАФИЧЕСКИЙ РОСТ
В демографических исследованиях изучаются изменения возрастной структуры народонаселения. В действительности мужья и жены часто принадлежат к разным возрастным группам, и деторождение зависит как от этого фактора, так и от индивидуальной способности женщин к деторождению. Однако в математической модели, которая будет здесь рассмотрена, детей классифицируют лишь по возрастным группам матерей. При таком способе анализа удобнее всего представлять изменения, происходящие за определенный период, в виде таблицы.
Обозначим возрастную структуру населения на время переписи 1940г тремя величинами – А40, В40, С40. Тогда А55, В55, С55 будут удовлетворять следующим соотношениям:
Величины, стоящие в круглых скобках в первом соотношении, естественно назвать коэффициентами рождаемости, а величины, стоящие во втором и третьем выражении, - коэффициентами выживаемости. Если предположить, что эти коэффициенты не изменяются во время прогнозирования, то полученные соотношения позволяют прогнозировать возрастной состав с шагом 15 лет. Разумеется, такая постоянность коэффициентов весьма малоправдоподобна, так как рождаемость и смертность зависят либо от случайных, либо от систематически действующих факторов или же от тех и других одновременно. Поэтому исследователь, стремясь приблизиться к реальности, может вводить переменные коэффициенты. Этот процесс приводит к усложнению модели. Методы, применяемые демографами, могут быть распространены на изучение проблем, касающихся экологии и эпидемиологии. Точно так же можно прогнозировать развитие популяций. Состоящих из неодушевленных предметов, таких, как телеграфные столбы, железнодорожные вагоны или жилые дома. В таких случаях нормы рождаемости заменяются нормами вложений, а показатель смертности – показателем износа. При этом модель показывает необходимое пополнение или замену, обеспечивающую надлежащий запас в течение любого желаемого отрезка времени.
Запишем соотношения (21) в матричном виде: SX40=X55, где
Предположив постоянство матрицы S, можно прогнозировать на любой период: SX40=X55; SX55=X70; SX70=X85… или S3X40=X85…S¥X40=X¥. Рассмотрим вопрос о предельном состоянии возрастной структуры Х¥. Очевидно, что это связано с изучением матрицы S¥. Для простоты предположим, что матрица S приводится к диагональному виду, т.е. существует матрица Т, такая, что S=TLT-1. L = Diag (l1, l2 … ln). Тогда Sk=TLkT-1. Пусть
Пусть Т1 – собственный столбец, отвечающий собственному значению l1, а Y – первая строка матрицы Т-1. С учетом этого
где число
Упражнения 1. Какой процесс при вычислении предельного состояния выгоднее с точки зрения вычислительной работы: SXk = Xk+1 или SkX.
РЕГРЕССИОННЫЕ МОДЕЛИ
В экономике часто необходимо определить наилучшую формулу, связывающую одну переменную с некоторыми другими переменными. В этом случае обычно начинают с предположения, что существует линейная связь между «зависимой» и «независимой» переменными. Например, если y является зависимой переменной и х1, х2, …, хn – независимые переменные, то соотношение вида
может быть использовано для выражения у через хi. Коэффициенты ai предполагаются постоянными, а зависимость (22) называют регрессионной модель. Наилучшие значения ai могут быть подобраны исходя из исторических экспериментальных данных. Например, для предсказания того, как темпы развития инфляции меняются от уровня безработицы, можно было бы взять такую модель: когда уровень безработицы равен нулю, темпы инфляции составляют b0 процентов, а когда безработица составляет х процентов, то инфляция составляет b0+b1x процентов. Таким образом, за i-й промежуток времени
уi = b0+b1xi, i = 1,…, m. (23) Имея исторические данные уi, хi, можно попытаться подобрать наилучшие значения b0 и b1. Существует несколько способов нахождения b0 и b1, но наиболее удобным является метод наименьших квадратов. Понятие нормы матрицы дает нам возможность пересмотреть и обобщить понятие решения системы линейных уравнений. Напомним, что под классическим понятием решения матричного уравнения АХ=В (24) мы понимаем матрицу К, которая, после подстановки ее вместо Х, обращает уравнение в тождество. Однако для уравнения (24), согласно теореме Кронекера-Капелли, такой матрицы К может не существовать. Такая ситуация часто возникает в регрессионных моделях, где мы имеем ело с сильно переопределенными системами. Используя понятие нормы, можно обойти указанную трудность, изменив само понятие «классическое решение». Буем понимать под обобщенным решением уравнения (24) матрицу V, которая доставляет минимальное значение норме невязки АХ – В, т.е.
Однако способы задания нормы могут привести к серьезным вычислительным трудностям при решении задачи (25). Наиболее просто проблема выглядит для 2-нормы. Критерий (25) получил название метода наименьших квадратов (МНК), если учесть, что
Покажем, что МНК – решение всегда существует и укажем способ его нахождения. Представим матрицу
В = СВ+(Е - С)В, где С = А(АТА)-1АТ, предположив, что матрица (АТА)-1 существует. Проведем вычисления
Второе слагаемое равно нулю так как АТ(Е-С)=АТ - АТА(АТА)-1АТ = АТ - АТ=0. Отсюда
Выражение Х = (АТА)-1АТВ. (26) Таким образом, мы установили, что МНК – решение существует и является единственным, если существует матрица (АТА)-1.
Упражнения 1. Привести вид всех матриц в выражении (26) для определения b0, b1 регрессионной модели (23). 2. Доказать cond(ATA) ³ cond A.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.18.167 (0.012 с.) |

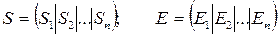 .
.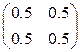 ; б)
; б) 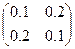 ; в)
; в) 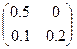 .
.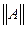 называется нормой матрицы А, если выполнены следующие свойства:
называется нормой матрицы А, если выполнены следующие свойства: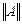 > 0, если А ≠ 0;
> 0, если А ≠ 0;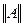 = 0, если А = 0;
= 0, если А = 0;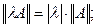


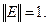

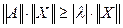
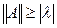 . (16)
. (16)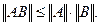
 .
.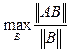
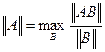 .
.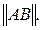
 и выбора размеров матрицы В. Если В матрица-столбец, то АВ также будет матрицей-столбом. Выберем для матрицы-столбца
и выбора размеров матрицы В. Если В матрица-столбец, то АВ также будет матрицей-столбом. Выберем для матрицы-столбца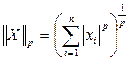 .
.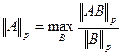 .
. :
: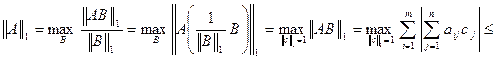
 .
.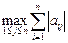 достигается при j=k.
достигается при j=k.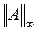 .
.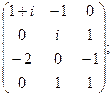 б)
б) 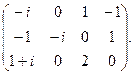
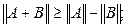
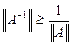 .
.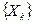 , которая получается с помощью итерационной формулы:
, которая получается с помощью итерационной формулы: (18)
(18) и укажем условия сходимости к решению Х уравнения (17). Вычтем Х из левой и правой части соотношения (18):
и укажем условия сходимости к решению Х уравнения (17). Вычтем Х из левой и правой части соотношения (18):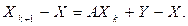
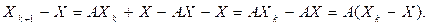

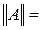 q<1, то получим
q<1, то получим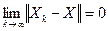 .
.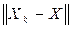 к нулю, запишем цепочку неравенств, обозначив
к нулю, запишем цепочку неравенств, обозначив 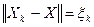 :
: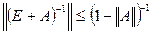 , если
, если 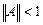 .
.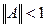 дает невырожденность матрицы (Е+А). действительно, соотношение (16) дает
дает невырожденность матрицы (Е+А). действительно, соотношение (16) дает 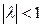 . Применяя Жорданово разложение матрицы, получим
. Применяя Жорданово разложение матрицы, получим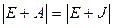 . Треугольная матрица Е+J не имеет нулей на главной диагонали и, следовательно,
. Треугольная матрица Е+J не имеет нулей на главной диагонали и, следовательно, 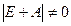 .
.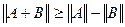 , то
, то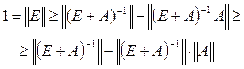 .
. .
. .
.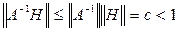 .
. .
.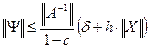 .
.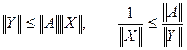 . С учетом этого
. С учетом этого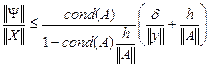 .
.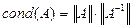 .
.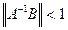 , то матрица А+В также невырождена.
, то матрица А+В также невырождена.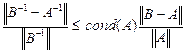 .
.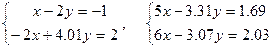 .
. (21)
(21) .
.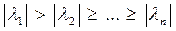 . Тогда
. Тогда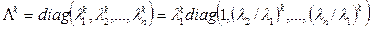 .
.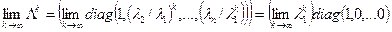 .
.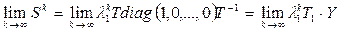 .
.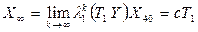 ,
,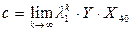 . Таким образом, предельное состояние возрастной структуры пропорционально собственному столбцу матрицы S, отвечающего максимальному собственному значению.
. Таким образом, предельное состояние возрастной структуры пропорционально собственному столбцу матрицы S, отвечающего максимальному собственному значению.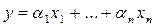 (22)
(22)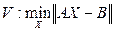 .
.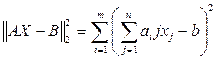 .
.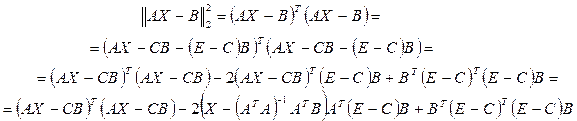 .
.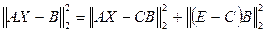 .
. не зависит от Х, а
не зависит от Х, а 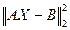 принимает минимальное значение, равное нулю, при
принимает минимальное значение, равное нулю, при


