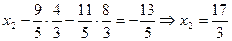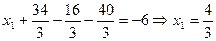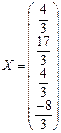Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения систем линейных алгебраических уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Все методы решения систем линейных алгебраических уравнений можно разделить на две группы: · точные методы; · методы последовательных приближений. С помощью точных методов, проделав конечное число операций, можно получить точные значения неизвестных. При этом предполагается, что коэффициенты и правые части системы известны точно, а все вычисления проводятся без округлений. К точным методам решения систем линейных алгебраических уравнений относятся такие методы как метод обратной матрицы, метод Крамера (определителей), метод Гаусса и др. Точные методы решения систем линейных алгебраических уравнений применяют для решения систем относительно небольшой размерности (до Система линейных алгебраических уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Решить систему линейных алгебраических уравнений - значит определить, является ли она совместной или нет. В случае если система совместна, нужно найти ее решение. Для определения совместности системы можно использовать теорему Кронекера - Капелли, смысл которой состоит в следующем: для того, чтобы система линейных алгебраических уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы коэффициентов системы Решение систем линейных алгебраических уравнений Методом Гаусса В электроэнергетических задачах наибольшее распространение получил метод последовательных исключений Гаусса. Он относится к классу точных методов решения систем линейных алгебраических уравнений. Процесс решения по методу Гаусса состоит из двух этапов: прямой ход метода и обратный ход. На первом этапе (прямой ход) система приводится к треугольному виду, на втором этапе (обратный ход) идет последовательное определение неизвестных из этой треугольной системы. Пусть дана система линейных алгебраических уравнений
Будем считать, что коэффициент
Прибавим теперь к каждому Преобразованная система примет вид:
Здесь индекс Переходя, к выполнению второго шага прямого хода метода Гаусса предположим, что элемент
Прибавим к Проведя далее аналогичные преобразования, после
Второй этап – обратный ход метода Гаусса реализуется следующим образом. Из последнего уравнения системы (4) определяем Отметим некоторые специфические особенности изложенного метода Гаусса, характерные для ЭЭС. Основная из них заключается в погрешностях вычислений в результате округления чисел по причине конечной длины разрядной сетки ПК. Погрешности зависят в основном от величины ведущего элемента. На шаге исключения, прямого хода метода Гаусса погрешности возрастают, если ведущий элемент мал по сравнению с другими коэффициентами соответствующего столбца матрицы коэффициентов Пример: для заданной системы линейных алгебраических уравнений найти решение методом Гаусса.
В начале исследуем заданную систему на совместность. Для этого вычислим ранг матрицы коэффициентов >> A=[2, -1, 1, -1;2, -1, 0,-3;3 -1, 1, 1;1, 2, -4, 5]; rank(A) ans = 4 >> A1=[2, -1, 1, -1, 1; 2,- 1, 0,- 3,5;3,-1, 1, 1, -3;1, 2, -4, 5, -6]; rank(A1) ans = 4 Получили, что ранг матрицы коэффициентов равен рангу расширенной матрицы коэффициентов, отсюда следует, что система совместна и имеет единственное решение (ранги матриц равны порядку системы). Проведем преобразования по прямому ходу метода Гаусса
На главной диагонали, преобразованной матрицы коэффициентов, стоят 1. Теперь проведем преобразования в соответствии с обратным ходом метода Гаусса. Из последнего уравнения системы определяем
В результате получаем вектор-столбец искомых неизвестных
|
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 ). Привлекательными в методах последовательных приближений является их самоисправляемость и простота реализации на ПК. Для начала вычислений требуется задание начальных приближений для искомых неизвестных. К числу методов последовательных приближений относятся: метод простой итерации, метод Зейделя, метод релаксации и др.
). Привлекательными в методах последовательных приближений является их самоисправляемость и простота реализации на ПК. Для начала вычислений требуется задание начальных приближений для искомых неизвестных. К числу методов последовательных приближений относятся: метод простой итерации, метод Зейделя, метод релаксации и др.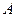 был равен рангу ее расширенной матрицы коэффициентов.
был равен рангу ее расширенной матрицы коэффициентов.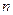 - го порядка.
- го порядка.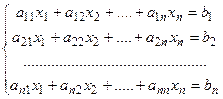 (2)
(2)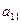 , который называют ведущим элементом первого шага, отличен от нуля (в случае, если
, который называют ведущим элементом первого шага, отличен от нуля (в случае, если 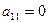 , нужно поменять местами первое уравнение с
, нужно поменять местами первое уравнение с 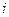 - тым уравнением, в котором
- тым уравнением, в котором 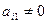 ). Разделим теперь почленно первое уравнение системы на коэффициент
). Разделим теперь почленно первое уравнение системы на коэффициент 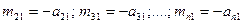 .
.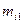 . Проделав эту операцию, мы исключим неизвестное
. Проделав эту операцию, мы исключим неизвестное 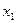 из всех уравнений, начиная со второго.
из всех уравнений, начиная со второго.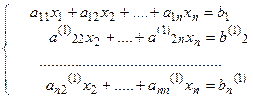 (3)
(3)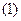 означает новые значения коэффициентов и правых частей, которые получаются после выполнения первого шага прямого хода метода Гаусса.
означает новые значения коэффициентов и правых частей, которые получаются после выполнения первого шага прямого хода метода Гаусса.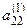 , который называют ведущим элементом второго шага, не равен нулю. Разделим второе уравнение на коэффициент
, который называют ведущим элементом второго шага, не равен нулю. Разделим второе уравнение на коэффициент 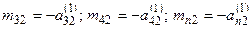
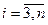 второе уравнение, умноженное на
второе уравнение, умноженное на 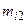 , в результате исключим неизвестное
, в результате исключим неизвестное 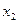 из всех уравнений, кроме первых двух.
из всех уравнений, кроме первых двух.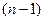 - го шага придем к треугольной системе вида:
- го шага придем к треугольной системе вида: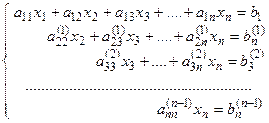 (4)
(4)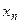 . По найденному значению
. По найденному значению 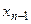 . Затем по значениям
. Затем по значениям 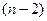 - го уравнения находим
- го уравнения находим 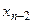 и т.д. Последовательное вычисление неизвестных продолжается до тех пор, пока из первого уравнения системы (4) не определим
и т.д. Последовательное вычисление неизвестных продолжается до тех пор, пока из первого уравнения системы (4) не определим 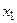 . На этом процесс решения заканчивается.
. На этом процесс решения заканчивается.
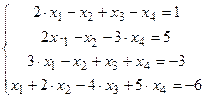
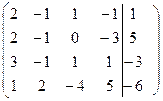
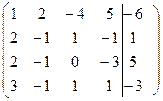
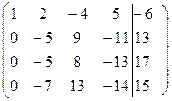
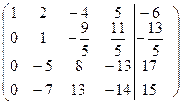
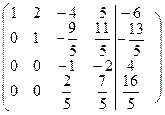
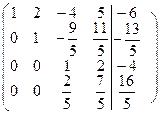
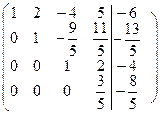
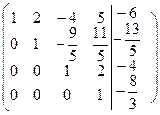
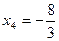 . Из предпоследнего уравнения находим
. Из предпоследнего уравнения находим 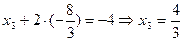 . Проведя аналогичные вычисления, получаем
. Проведя аналогичные вычисления, получаем