
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенные методы решения нелинейных алгебраических уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Необходимость отыскания корней характеристического уравнения всегда возникает при расчете переходного процесса в линейных электрических цепях. В общем случае характеристическое уравнение может быть сколь угодно высокого порядка. Значения, которые могут принимать корни характеристического уравнения дают представление о характере переходного процесса и в общем случае могут принимать комплексные значения. Алгебраическое уравнение
Относительно небольшое количество задач отыскания корней нелинейных алгебраических уравнений можно решить аналитически, на практике почти всегда приходится находить решение уравнений с помощью численных методов. Приближенное решение нелинейных алгебраических уравнений состоит из двух этапов: · этап отделения корней · этап уточнения корней Пусть требуется найти корни уравнения · Графический способ. Приближенно строится график функции · Табличный способ. Строится таблица, состоящая из двух строк, в первой строке с каким-то произвольным шагом изменяется значение аргумента · Способ нахождения верхних и нижних границ положительных и отрицательных корней. Метод деления отрезка пополам После отделения корней можно уточнить его одним из методов последовательных приближений. Одним из таких методов является метод деления отрезка пополам. Этот метод является наиболее простым надежным методом уточнения корня на отрезке
Рис. 4 Очевидно, что середина отрезка Пример: уточнить корень уравнения 1. Находим
Отсюда следует, что корень находится на отрезке Длина этого отрезка 2. Находим
Отсюда следует, что корень находится на отрезке Длина этого отрезка 3. Находим
Отсюда следует, что корень находится на отрезке Длина этого отрезка 4. Находим
Отсюда следует, что корень находится на отрезке Длина этого отрезка 5. Находим
Отсюда следует, что корень находится на отрезке Длина этого отрезка 6. Находим
Отсюда следует, что корень находится на отрезке Длина этого отрезка Середина отрезка
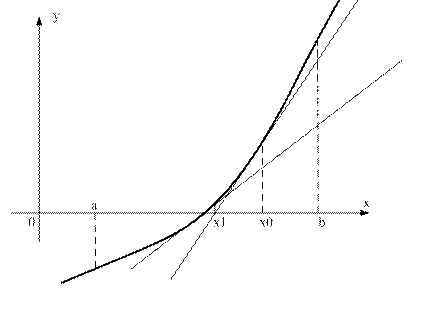
Метод Ньютона Метод Ньютона применяется к решению уравнения, когда функция
Рис. 5 Для начала вычислений требуется задание одного начального приближения
Общая формула метода Ньютона может быть записана с помощью рекуррентного соотношения:
где Каждое последующее приближение вычисляется через предыдущее. Геометрически точка На практике можно встреться со случаем сходимости метода Ньютона, когда
а сомножители
Сомножители Условием выхода из итерационного процесса по методу Ньютона является выполнение неравенства Пример: уточнить корень уравнения Выберем в качестве начального приближения 1. По рекуррентной формуле метода Ньютона вычислим
2. По рекуррентной формуле метода Ньютона вычислим
Метод простой итерации Метод простой итерации применяется к решению уравнения с выделенным значением неизвестного в правой части
Если Условием сходимости процесса итераций, т.е. условие существования предела есть соблюдение неравенства, носящего название принципа сжатых отображений:
где
что позволяет отнести метод простой итерации к классу методов с линейной скоростью сходимости. Во всех итерационных методах уточнения корней уравнений в качестве критерия окончания процесса вычислений выбрано условие:
При этом предполагается, что чем больше проделано уточнений, тем выше точность определения корня. Метод простой итерации имеет линейную скорость сходимости, чтобы увеличить скорость сходимости следует выбирать достаточно близкие значения интервала отделения корня Следует четко уяснить, что во всех итерационных методах есть условие входа в итерационный процесс и условие выхода из итерационного процесса, в противном случае он может продолжаться бесконечно, бесконечно близко можно приближаться к точному решению, но в общем случае точное решение не достижимо. Пример: уточнить корень уравнения Преобразуем заданное уравнение применительно к методу простой итерации. Оставим слагаемое
Проверяем принцип сжатых отображений для выбранной нами итерирующей функции (рассматриваем один из множества возможных способов представления итерирующей функции). Проанализируем, как ведет себя функция Построим таблицу
Из таблицы видно, что концы отрезка, на котором выполняется условие Таким образом будем уточнять корень на отрезке
Выберем в качестве начального приближения Сведем расчеты в таблицу Таблица 5
На 15 шаге выполняется условие выхода из итерационного процесса
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 - ной степени задается в следующем виде:
- ной степени задается в следующем виде: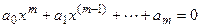
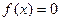 . Этап отделения корней этого уравнения заключается в нахождении всех интервалов в области определения функции
. Этап отделения корней этого уравнения заключается в нахождении всех интервалов в области определения функции 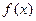 , на концах которых функция меняет знак. Количество интервалов определяется по числу корней. Не существует универсального метода, позволяющего отделить все корни нелинейного алгебраического уравнения. В качестве возможных способов отделения корней могут быть предложены следующие способы.
, на концах которых функция меняет знак. Количество интервалов определяется по числу корней. Не существует универсального метода, позволяющего отделить все корни нелинейного алгебраического уравнения. В качестве возможных способов отделения корней могут быть предложены следующие способы.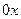 , на которых функция
, на которых функция 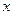 , желательно на отрезке симметричном относительно
, желательно на отрезке симметричном относительно  . Во второй строке вычисляются соответствующие значения функции
. Во второй строке вычисляются соответствующие значения функции  в том случае, когда функция
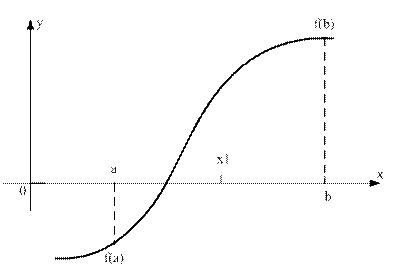
в том случае, когда функция 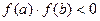 .
.
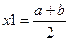 . В этой точке определяется знак функции
. В этой точке определяется знак функции 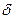 , то деление отрезка пополам продолжается до тех пор, пока длина последнего отрезка содержащего корень не станет меньше величины
, то деление отрезка пополам продолжается до тех пор, пока длина последнего отрезка содержащего корень не станет меньше величины 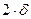 . Тогда середина последнего отрезка даст значение корня с требуемой точностью. В этом методе можно не вычислять само значение функции
. Тогда середина последнего отрезка даст значение корня с требуемой точностью. В этом методе можно не вычислять само значение функции 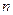 шаге через
шаге через 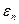
 , где
, где 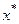 - точное значение корня, тогда погрешности на
- точное значение корня, тогда погрешности на 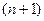 шаге связаны неравенством
шаге связаны неравенством  , где
, где 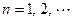 , что позволяет отнести метод деления отрезка пополам к методам, имеющим линейную скорость сходимости.
, что позволяет отнести метод деления отрезка пополам к методам, имеющим линейную скорость сходимости. , находящийся на
, находящийся на 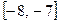 методом деления отрезка пополам с точностью
методом деления отрезка пополам с точностью  .
.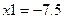 . Вычисляем значения функции в точке
. Вычисляем значения функции в точке

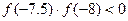
 .
.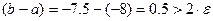
 процесс по методу деления отрезка пополам следует продолжить.
процесс по методу деления отрезка пополам следует продолжить.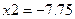 . Вычисляем значения функции в точке
. Вычисляем значения функции в точке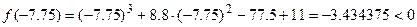
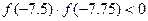
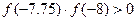
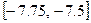 .
.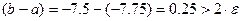
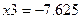 . Вычисляем значения функции в точке
. Вычисляем значения функции в точке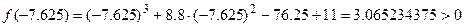
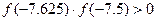

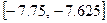 .
.
 . Вычисляем значения функции в точке
. Вычисляем значения функции в точке


 .
.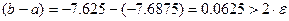
 . Вычисляем значения функции в точке
. Вычисляем значения функции в точке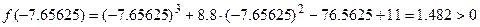
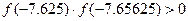
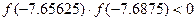
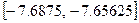 .
.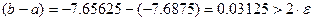
 . Вычисляем значения функции в точке
. Вычисляем значения функции в точке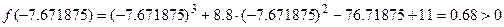
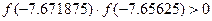
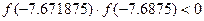
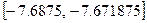 .
.
 .
.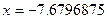
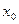 внутри отрезка
внутри отрезка 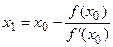
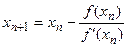 ,
,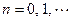 и
и 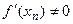 .
. является значением абсциссы точки пересечения касательной к кривой
является значением абсциссы точки пересечения касательной к кривой 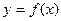 в точке
в точке 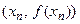 с осью абсцисс, поэтому часто метод Ньютона называют также методом касательных.
с осью абсцисс, поэтому часто метод Ньютона называют также методом касательных. далеко от искомого корня, так и со случаем расходимости метода для
далеко от искомого корня, так и со случаем расходимости метода для 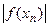 . В таком случае вычисления можно проводить по модифицированному методу Ньютона:
. В таком случае вычисления можно проводить по модифицированному методу Ньютона: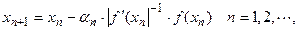
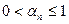 выбираются так, чтобы выполнялось неравенство
выбираются так, чтобы выполнялось неравенство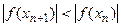 .
.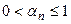 сжимают отображение. Рекомендуется всегда выбирать достаточно тесные границы корня
сжимают отображение. Рекомендуется всегда выбирать достаточно тесные границы корня 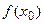 и ее кривизны
и ее кривизны 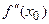 совпадают.
совпадают.
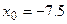 ,
, 
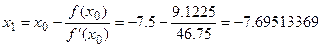
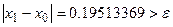


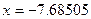
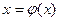 и состоит в построении последовательности
и состоит в построении последовательности 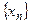 , начиная с некоторого начального значения
, начиная с некоторого начального значения 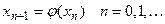
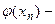 непрерывная функция, а
непрерывная функция, а 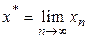 является корнем уравнения.
является корнем уравнения.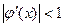 ,
,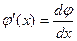 для всех
для всех 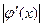 . Погрешности метода на
. Погрешности метода на 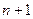 связаны неравенством
связаны неравенством ,
, , находящийся на
, находящийся на 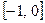 методом простой итерации с точностью
методом простой итерации с точностью 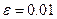 .
. в левой части уравнения, остальные слагаемые перенесем в правую часть с противоположными знаками.
в левой части уравнения, остальные слагаемые перенесем в правую часть с противоположными знаками.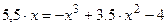

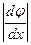 на отрезке
на отрезке 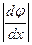
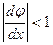 , соответственно равны
, соответственно равны 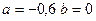 .
.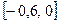 с помощью следующего рекуррентного уравнения
с помощью следующего рекуррентного уравнения .
.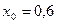
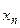
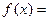

 . Отсюда следует, что корень уравнения найденный по методу простой итерации с точностью
. Отсюда следует, что корень уравнения найденный по методу простой итерации с точностью 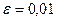
 равен
равен 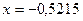 .
.


