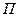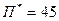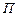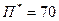Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прогнозирование уровня электропотребления на промышленном предприятииСодержание книги
Поиск на нашем сайте
По результатам наблюдений за выработкой продукции завода и потребляемой им электроэнергии из системы в течение
Пример: по результатам наблюдений за выработкой продукции завода и потребляемой этим заводом энергии из системы в течении шести лет получена количественная зависимость производства продукции П от потребляемой электроэнергии W.
Через два года намечается увеличение выработки продукции до 150 условных единиц в год. Определить какое количество энергии будет потребляться из системы в этот расчётный год.
где
При увеличении выработки продукции до 150 условных единиц в год из системы будет потребляться 441,6 МВт.ч.
Вычисление числовых характеристик случайных величин в системе MATLAB Никакой анализ статистических данных не может обойтись без предварительной их обработки: max (A), min(A) - поиск экстремальных элементов по столбцам массива А; max(A,B), min(A,B) - формирование массива с элементами, равными экстремальным из соответствующих элементов массивов; mean(X), mean (X,dim) -средние значения, в случае равновозможных значений случайной величины дискретного типа с помощью этих функций вычисляют математическое ожидание. std(X), std(X,flag), std(X,flag,dim) - стандартное отклонение (flag=0 -несмещенная оценка ; flag=1 - смещенная оценка s):
Для статистической обработки в MATLAB-е имеются две основные функции для вычисления ковариации и коэффициентов корреляции: · cov - в случае вектора данных эта функция выдает дисперсию, то есть меру распределения (отклонения) наблюдаемой переменной от ее среднего значения · corrcoef (X,Y) - коэффициенты корреляции, нормализованная мера линейной вероятностной зависимости между переменными.
Покажем применение стандартных статистических функций системы MATLAB на примере решения задачи из предыдущего примера. >> A=[35 21 78 80 100 69] A = 35 21 78 80 100 69 >> W=[150 100 250 300 300 200] W = 150 100 250 300 300 200 >> mean(A) ans = 6.3833e+001 >> mean(W) ans = 2.1667e+002 >> std(A,1) ans = 2.7273e+001 >> std(W,1) ans = 7.4536e+001 >> corrcoef(A,W) ans = 1.0000e+000 9.5654e-001 9.5654e-001 1.0000e+00 Индивидуальные задания Для промышленного предприятия в течении 1. Годовое потребление электроэнергии 2. Производство продукции Через 2 года намечается увеличение выпуска продукции до величины Таблица 7
Продолжение табл. 7
Продолжение табл. 7
Окончание табл. 7
Содержание соответствующего раздела В пояснительной записке Данный раздел должен содержать: · краткие теоретические сведения, · вычисление числовых характеристик случайных величин аналитически, · вычисление числовых характеристик случайных величин в системе MATLAB, · вычисление прогнозируемого значения электропотребления промышленного предприятия с помощью уравнения линейной регрессии.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Электрические системы. Математические задачи электроэнергетики /Под ред. В.А. Веникова. Т.1 – М.: Высшая школа, 1981. – 334с. 2. Курбацкий В.Г., Томин Н. В. Математические задачи электроэнергетики Ч.1: учеб. пособие для вузов / Курбацкий В.Г. и др. - ГОУ ВПО «БрГУ», 2007.- 142 с. 3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / Гмурман В.Е. - М.: Высшая школа, 2001. - 400 с. 4. Кривелев А.В. Основы компьютерной математики с использованием MATLAB: учеб. пособие для вузов / Кривелев А.В. - М.: Лекс - Книга, 2005. - 496 с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.011 с.) |

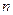 лет получена количественная зависимость
лет получена количественная зависимость  , отраженная в таблице. Здесь
, отраженная в таблице. Здесь  объем произведенной продукции в некоторых условных единицах,
объем произведенной продукции в некоторых условных единицах,  - объем потребленной электроэнергии в МВт.ч. Через год намечается увеличение выпуска продукции до некоторой конкретной величины. Требуется определить, какое количество электроэнергии будет потреблено из системы в этот расчетный год. Для прогноза следует использовать линейное уравнение регрессии
- объем потребленной электроэнергии в МВт.ч. Через год намечается увеличение выпуска продукции до некоторой конкретной величины. Требуется определить, какое количество электроэнергии будет потреблено из системы в этот расчетный год. Для прогноза следует использовать линейное уравнение регрессии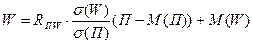 .
. Данное уравнение носит название линейного уравнения регрессии, т.к. зависимость между функцией
Данное уравнение носит название линейного уравнения регрессии, т.к. зависимость между функцией  .
.


 ;
;  ;
;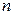 лет собирались статистические данные:
лет собирались статистические данные:
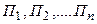
 . Спрогнозировать годовое потребление электроэнергии на этот расчетный год. Исходные данные по вариантам приведены в таблице.
. Спрогнозировать годовое потребление электроэнергии на этот расчетный год. Исходные данные по вариантам приведены в таблице.