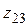Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические Задачи электроэнергетикиСодержание книги
Поиск на нашем сайте
Иркутский государственный техническИЙ УНИВЕРСИТЕТ
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ЭЛЕКТРОЭНЕРГЕТИКИ
Программа, методические указания и задания для выполнения курсовой работы по направлению подготовки: 140400 «Электроэнергетика и электротехника» для студентов квалификации бакалавр Заочной формы обучения
ИЗДАТЕЛЬСТВО Иркутского государственного технического университета Иркутск—2011 Математические задачи электроэнергетики: программа, метод. указания и задания для выполнения курсовой работы. / Составители: О.В. Свеженцева - Иркутск: Изд-во ИрГТУ, 2011 – 56 с.
Содержат краткие теоретические сведения по курсу «Математические задачи электроэнергетики», программу курса, индивидуальные задания и методические указания по порядку выполнения и оформления курсовой работы. Предназначены для студентов квалификации бакалавр, обучающихся по направлению подготовки: 140400 «Электроэнергетика и электротехника» заочной формы обучения Иркутского государственного технического университета.
Библиогр. 4 назв. Ил. 7. Табл. 7.
Рецензент: канд. техн. наук, доцент кафедры ЭССиС ИрГТУ Л.А. Акишин
ОГЛАВЛЕНИЕ ПРОГРАММА КУРСА……………………………………………………………...4 ОБЩИЕ ПОЛОЖЕНИЯ О КУРСОВОЙ РАБОТЕ………………………………...5 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОНЕНИЮ КУРСОВОЙ РАБОТЫ…………………………………...................................................................7 1. Математическое моделирование задач электроэнергетики с помощью аппарата линейной алгебры и теории графов……………………………….7 1.1. Представление синусоидального тока комплексными величинами……………………………………………………………..7 1.2. Матричная алгебра………………………………………………...8 1.3. Определитель матрицы и его свойства…………………………10 1.4. Вычисление обратной матрицы…………………………………12 1.5. Решение задач линейной алгебры в системе MATLAB……….13 2. Расчет установившихся режимов электрических систем ……………...16 2.1. Схема замещения электрической сети как связный граф……..16 2.2. Первая и вторая матрицы инциденций…………………………19 2.3.Матричная форма записи уравнений состояния электрической сети…………………………………………………...20 3. Методы решения систем линейных алгебраических уравнений............27
3.1. Решение систем линейных алгебраических уравнений Методом Гаусса……………………………………………………….28 3.2. Решение систем линейных алгебраических уравнений в системе MATLAB…………………………………………………….31 4. Приближенные методы решения нелинейных алгебраических уравнений…………………………………………………………………….35 4.1. Метод деления отрезка пополам………………………………..36 4.2. Метод Ньютона…………………………………………………..38 4.3. Метод простой итерации………………………………………...40 4.4. Решение нелинейных алгебраических уравнений в системе MATLAB………………………………………………………………42 5.Применение вероятностно – статистических методов в задачах электроснабжения…………………………………………………………...46 5.1. Основные определения………………………………………….46 5.2. Прогнозирование уровня электропотребления на промышленном предприятии………………………………………..48 5.3.Вычисление числовых характеристик случайных величин в системе MATLAB…………………………………………………….50 БИБЛИОГРАФИЧЕСКИЙ СПИСОК……………………………………………..55
ПРОГРАММА КУРСА Введение Задачи дисциплины, ее содержание и связь со смежными и специальными дисциплинами. Общие сведения о системах электроснабжения. Режимы работы систем электроснабжения, основные показатели режимов работы. Задачи, возникающие при проектировании и эксплуатации систем электроснабжения. Система электроснабжения как объект математического исследования. Использование комплексных величин и матричной алгебры в электроэнергетике Три формы представления комплексных чисел. Правила выполнения арифметических действий над комплексными числами. Представление синусоидального тока комплексными величинами. Комплексное сопротивление, комплексная проводимость. Матрицы и их преобразования. Основные определения. Матричная алгебра. Определитель матрицы. Матричная форма записи и решения системы линейных алгебраических уравнений. Общие сведения об обратных матрицах. Особенные и неособенные матрицы. Способы определения обратных матриц: классический метод (с помощью определителей), метод итераций. Применение теории графов для расчета электрических сетей
Общие понятия о графах, направленный граф, его основные элементы. Первая матрица инциденций - матрица соединений по узлам схемы. Составление матриц соединений для замкнутых и разомкнутых схем замещения. Матрица коэффициентов токов, способы ее составления. Применение матриц соединения и коэффициентов распределения токов. Дерево и хорды направленного графа. Вторая матрица инциденций - матрица соединений по контурам схемы. Составление матриц контуров для замкнутых схем замещения, а также для дерева и хорд. Правило рациональной нумерации ветвей и контуров в направленном графе. Применение матриц контуров. Соотношения между матрицами соединений и контуров. Обобщенное уравнение состояния электрической сети и способы его решения Обобщенное уравнение состояния электрической сети. Независимые параметры схемы замещения: независимые токи ветвей и независимые падения напряжений в ветвях. Определение независимых параметров в схемах замещения при наличии и отсутствии взаимных сопротивлений между ветвями дерева и хордами. Применение метода разделения: матриц на блоки для преобразования уравнений состояния. Расчет параметров электрической сети в установившемся режиме методом преобразования уравнений состояния. Применение узловых уравнений при наличии узловых токов в схемах замещения. Матрицы узловых проводимостей и узловых сопротивлений, способы их определения. Применение контурных уравнений при наличии в схеме источников ЭДС, при наличии источников ЭДС и узловых токов, при наличии только узловых токов. Матрицы контурных сопротивлений и контурных проводимостей, способы их определения. Методы расчета установившегося режима Прямые методы расчета установившегося режима. Метод обратной матрицы. Метод Гаусса. Метод Гаусса-Зейделя. Итерационные методы расчета установившегося режима. Метод простой итерации. Метод Ньютона. Применение методов теории вероятностей в электроэнергетике Случайные события в энергетике. Классическое и статистическое определения вероятности случайных событий. Законы теории вероятностей для независимых и зависимых случайных событий. Случайные величины в энергетике. Дискретные и непрерывные величины. Вероятностные характеристики случайных величин: функции распределения и плотности распределения. Числовые характеристики случайных величин: математическое ожидание, дисперсия, среднеквадратическое отклонение. Применение методов математической статистики в электроэнергетике Статические ряды и их характеристики: медиана, мода, среднее арифметическое, размах вариации, дисперсия, среднеквадратическое отклонение. Практические методы вычисления этих характеристик. Функциональные и корреляционные зависимости. Линейная корреляция. Коэффициент корреляции и коэффициенты регрессии. Нелинейная корреляция, корреляционные отношения и их свойства. Множественная корреляция, совокупный коэффициент корреляции. Применение корреляционного анализа для изучения закономерностей электропотребления. ОБЩИЕ ПОЛОЖЕНИЯ О КУРСОВОЙ РАБОТЕ Данная работа обобщает все знания, полученные при изучении курса «Математические задачи электроэнергетики», поэтому естественно, что она включает в себя перечень основных задач, составляющих содержание данного курса. Курсовая работа по дисциплине «Математические задачи электроэнергетики» состоит из двух основных составных частей:
· математическое моделирование задач электроэнергетики с помощью аппарата линейной алгебры и теории графов, · стохастическое моделирование задач электроэнергетики. Особенностью выполнения данной курсовой работы является использование для ее выполнения систем компьютерной математики. Студент в ходе работы над данным курсовым проектом выполняет каждое задание двумя способами: 1. решает задачу аналитическим способом, 2. решает задачу в системе компьютерной математики MATLAB. Современная компьютерная математика предлагает целый набор интегрированных программных систем и пакетов программ для автоматизации математических расчетов. MATLAB — одна из систем автоматизации математических расчетов, построенная на расширенном представлении и применении матричных операций. Система MATLAB применима для практических расчетов в любой области науки и техники, в том числе в электроэнергетике. Курсовая работа выполняется и оформляется на листах стандартного формата А4, с обязательным закреплением их. Размеры полей: верхнего не менее 15 мм, нижнего не менее 20 мм, левое поле не менее 30 мм, правое – не менее 10 мм. Текст пояснительной записки должен быть выполнен с помощью печатающих устройств вывода ПК, шрифт Times New Roman, размер шрифта 14, межстрочный интервал «одинарный». Текст пояснительной записки должен быть кратким и четким. Все листы пояснительной записки должны быть пронумерованы арабскими цифрами, первым листом является титульный лист, далее должно идти содержание. Все формулы пишутся в отдельную строку с использованием редактора формул. Допускается внутри текста помещать короткие формулы с ранее расшифрованными символами. Числовые значения физических величин в формулу подставляются в той же последовательности, в какой они приведены в формуле. Единицу физической величины проставляют только у результата вычислений. Все формулы нумеруются арабскими цифрами в пределах раздела. Электрические схемы, графики, диаграммы выполняются с соблюдением требований ЕСКД и с использованием чертежных инструментов, допускается применение компьютерной графики. Рисунки необходимо пронумеровать, а в тексте поместить ссылки на них. Графические обозначения на схемах выполняются линиями той же толщины, что и линии связи. Электрические схемы выполняются в соответствии с ГОСТ 2.702. Список литературы включает все источники информации, используемые при выполнении курсовой работы. Литературу записывают в порядке появления ссылок на источник в пояснительной записке или в алфавитном порядке, но уже без ссылок. Нумерация источников должна быть сквозной. Ссылку на источник в тексте пояснительной записки дают в квадратных скобках.
В первом разделе курсовой работы «Математическое моделирование задач электроэнергетики с помощью аппарата линейной алгебры и теории графов» следует решить следующие задачи. · Задачи матричной алгебры. · Расчет установившегося режима разомкнутой электрической сети. · Расчет установившегося режима замкнутой электрической сети. · Решение системы линейных алгебраических уравнений методом Гаусса, методом Жордана - Гаусса. · Решение с заданной точностью Во втором разделе курсовой работы «Стохастическое моделирование задач электроэнергетики» следует решить задачу прогнозирования уровня электропотребления на промышленном предприятии по результатам наблюдений в течении ряда лет за динамикой выпуска продукции и электропотребления.
Матричная алгебра Матрицей размера
составленная из элементов Положение элементов в таблице определяется двойным индексом Если в матрице Квадратной матрицей называется матрица, в которой число строк совпадает с числом столбцов. Если элементы в квадратной матрице располагаются симметрично относительно главной диагонали, то такая матрица называется симметричной. Диагональной матрицей называется матрица, в которой все элементы, кроме стоящих на главной диагонали, равны 0. Единичная матрица, это диагональная матрица, у которой на главной диагонали стоят 0. Матричная алгебра это множество матриц плюс множество операций, которые можно выполнять над матрицами. В любой алгебре есть два замечательных числа – это ноль и единица. Ноль не изменяет число при сложении, единица не изменяет число при умножении, т.е.
В алгебре матриц также есть подобные элементы – это нулевая матрица, она играет роль нуля в алгебре матриц и это единичная матрица соответствующей размерности, она играет роль единицы в алгебре матриц. Сложение матриц. Складывать можно только матрицы, имеющие одинаковую размерность. Сложением двух матриц называется операция, при которой складываются элементы, стоящие на одинаковых местах в соответствующих таблицах. Пример:
Умножение матрицы на число. Для того чтобы умножить матрицу на число Пример:
Умножение матриц. Умножение матриц в алгебре матриц не коммутативно. Для того, чтобы произведение матриц существовало необходимо чтобы число столбцов первой матрицы равнялось числу строк второй матрицы. Если матрица
Так как произведение матриц не коммутативно, следует различать умножение матрицы Пример:
Вычисление обратной матрицы При решении матричных уравнений широко используют обратную матрицу. Она в известной степени заменяет операцию деления, которая в явном виде в алгебре матриц отсутствует. Квадратные матрицы одинакового порядка, произведение которых дает единичную матрицу
Вычислить обратную матрицу можно только для такой матрицы Классический алгоритм вычисления обратной матрицы 1. Записывают матрицу 2. Заменяют каждый элемент матрицы 3. Этот определитель сопровождают знаком плюс, если сумма индексов элемента четная, и знаком минус – в противном случае. 4. Делят полученную матрицу на Пример. Требуется вычислить обратную матрицу
Матрица
Заменим каждый элемент определителем, полученным при вычеркивании соответствующей строки и столбца:
Поменяем знаки у элементов с нечетной суммой индексов:
Разделим все элементы матрицы
Если теперь умножить полученную обратную матрицу на матрицу Содержание соответствующего раздела В пояснительной записке Данный раздел должен содержать: · краткие теоретические сведения, · вычисление определителя матрицы двумя аналитическими способами, · вычисление определителя в системе MATLAB, · вычисление обратной матрицы классическим способом, · вычисление обратной матрицы в системе MATLAB.
Рис. 2 Для схемы, представленной на рис.2 найти токи в ветвях разомкнутой электрической сети, используя матричную форму записи 1-го закона Кирхгофа. Токи нагрузки узлов равны Матрица задающих токов принимает вид
Матрица задающих токов равна матрице токов нагрузок, взятой с противоположным знаком. Выберем в качестве балансирующего узла
Из обобщенного уравнения состояния
Индивидуальные задания Для схемы, представленной на рис.2 найти токи в ветвях разомкнутой электрической сети, используя матричную форму записи 1-го закона Кирхгофа. Токи нагрузки заданы в таблице 2. Таблица 2 Исходные данные
Окончание табл. 2
Содержание соответствующего раздела В пояснительной записке Данный раздел должен содержать: · краткие теоретические сведения, · обобщенное уравнение состояния, · вычисление обратной матрицы для матрицы · вычисление обратной матрицы для матрицы · вычисление токов в ветвях аналитическим методом и с помощью MATLAB- программы, · вычисление напряжений в узлах аналитически, · вычисление напряжений в узлах в системе MATLAB. Пример. Для схемы представленной на рис.3 определить токи в ветвях схемы, напряжения в узлах. Сеть трехфазная. Токи нагрузки равны
Рис. 3 В начале составим первую и вторую матрицы инциденций (
Столбцы в этой матрицы можно условно пронумеровать как связи Первая матрица инциденций без балансирующего узла будет иметь вид:
В нашей схеме замещения всего один независимый контур, в соответствии с этим вторая матрица инциденций примет вид:
Столбцы в этой матрице имеет ту же нумерацию, что и в первой матрице инциденций. Запишем для нашей схемы обобщенное уравнение состояния
Последний элемент в вектор- столбце Найденные токи принимают значения
По закону Ома определим падение напряжения на ветвях схемы
Используя уравнение
Перемножая матрицы в матричном уравнении, получаем Индивидуальные задания Для схемы представленной на рис.3 определить токи в ветвях схемы, напряжения в узлах. Сеть трехфазная. Таблица 3 Исходные данные
Окончание табл. 3
Познавательные статьи:
|
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 2961; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.89.112 (0.011 с.) |

 нелинейного алгебраического уравнение методом деления отрезка пополам, методом Ньютона, методом простой итерации.
нелинейного алгебраического уравнение методом деления отрезка пополам, методом Ньютона, методом простой итерации.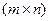 называется прямоугольная таблица
называется прямоугольная таблица ,
, и содержащая
и содержащая  строк и
строк и 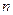 столбцов.
столбцов. , первый означает номер строки, второй номер столбца на пересечении которых стоит данный элемент. Запись группы величин в виде матрицы не предусматривает каких-либо действий над ними. Это лишь одна из форм упорядоченной записи в виде условной таблицы.
, первый означает номер строки, второй номер столбца на пересечении которых стоит данный элемент. Запись группы величин в виде матрицы не предусматривает каких-либо действий над ними. Это лишь одна из форм упорядоченной записи в виде условной таблицы.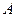 строки сделать столбцами, а столбцы строками, то получается транспонированная матрица
строки сделать столбцами, а столбцы строками, то получается транспонированная матрица  .
. .
.
 , необходимо каждый элемент этой матрицы умножить на число
, необходимо каждый элемент этой матрицы умножить на число 
 , а матрица
, а матрица  размерность
размерность  , то матрица
, то матрица  имеет размерность
имеет размерность  . В качестве элементов расположенных на пересечении
. В качестве элементов расположенных на пересечении 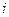 -той строки и
-той строки и  -го столбца матрицы произведения, принимают суммы попарных произведений, расположенных на одинаковых местах указанных строк матрицы – множимого и столбцов матрицы- множителя.
-го столбца матрицы произведения, принимают суммы попарных произведений, расположенных на одинаковых местах указанных строк матрицы – множимого и столбцов матрицы- множителя.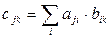
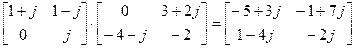
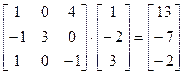
 , называются взаимообратными или обратными. Обозначается обратная матрица
, называются взаимообратными или обратными. Обозначается обратная матрица 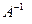 и для нее справедливо
и для нее справедливо .
. .
.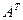 , транспонированную к матрице
, транспонированную к матрице  определитель матрицы
определитель матрицы 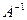
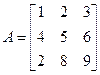 .
.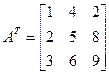 .
. .
.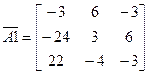
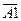 на
на 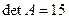 . В результате получаем обратную матрицу
. В результате получаем обратную матрицу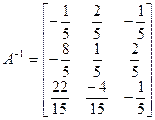 .
.
 .
.
 узел. Обозначим через
узел. Обозначим через  первую матрицу инциденций без балансирующего узла.
первую матрицу инциденций без балансирующего узла.


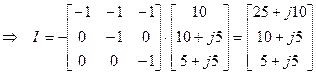
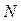


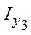


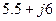
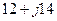
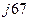


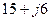





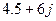




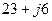
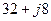

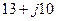








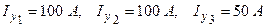 . Узел
. Узел  . Сопротивления ветвей схемы соответственно равны
. Сопротивления ветвей схемы соответственно равны  .
.
 ) для нашего графа.
) для нашего графа. , узел
, узел  . Связи однозначно определяют направление ветвей в схеме замещения, так например, связь
. Связи однозначно определяют направление ветвей в схеме замещения, так например, связь  означает что данная ветвь имеет направление из узла
означает что данная ветвь имеет направление из узла  в узел
в узел 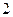 .
. .
. .
.

 .
. равен
равен  , т.к. ЭДС в ветвях отсутствует. Данная система может быть решена относительно искомых токов в ветвях любым методом решения систем линейных алгебраических уравнений (например, методом обратной матрицы или методом Гаусса).
, т.к. ЭДС в ветвях отсутствует. Данная система может быть решена относительно искомых токов в ветвях любым методом решения систем линейных алгебраических уравнений (например, методом обратной матрицы или методом Гаусса).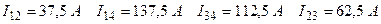 .
.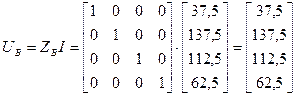
 , получаем
, получаем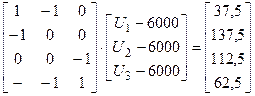 .
. неизвестными, т.е. данная система переопределена. В нашем случае можно выбросить любое уравнение переопределенной системы и решить ее также каким - либо методом решения систем линейных алгебраических уравнений. В результате получаем
неизвестными, т.е. данная система переопределена. В нашем случае можно выбросить любое уравнение переопределенной системы и решить ее также каким - либо методом решения систем линейных алгебраических уравнений. В результате получаем  .
.