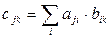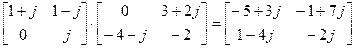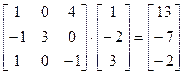Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания по выполнению курсовой работыСодержание книги
Поиск на нашем сайте
Математическое моделирование задач электроэнергетики с помощью аппарата линейной алгебры и теории графов. Представление синусоидального тока комплексными величинами Любое вещественное число можно изобразить графически на числовой оси 0х. Пусть на числовой оси выбрано положительное направление. От т.0, принятой за начало, отложим в определенном масштабе отрезок, длина которого пропорциональна рассматриваемому вещественному числу. Понятие вещественного числа можно обобщить, если ввести в рассмотрение число
Комплексные числа также можно изображать графически. Это изображение будет двумерным на плоскости, образованной двумя взаимно перпендикулярными осями 0х и 0у. Комплексное число на плоскости х0у представляется точкой
Любое комплексное число можно представить в одной из трех форм. · Алгебраической · Тригонометрической · Показательной
Где
Если аргумент
И графическое представление комплексной функции О.Комплексная функция Закон Ома для участка цепи синусоидального тока без источника ЭДС можно сформулировать таким образом: комплексная амплитуда тока в цепи синусоидального тока равна отношению комплексной амплитуды напряжения к комплексному сопротивлению цепи. Два комплексных числа
Т.е. другими словами два комплексных числа равны, когда равны их действительные и комплексные части.
Для алгебраической формы представления комплексных чисел справедливо; при сложении двух комплексных чисел складываются отдельно их действительные и комплексные части.
Умножение двух комплексных чисел следует производить как умножение двух алгебраических двучленов, приводя подобные при нулевой и первой степени числа
Если число Вычитание и деление определяются как операции обратные операциям сложения и умножения, деление на 0 для комплексного числа не определено. Деление комплексных чисел удобно выполнять с помощью умножения делимого и делителя на число сопряженное делителю. В результате этой, не изменяющей дробь операции, в знаменателе получаем вещественное число. Матричная алгебра Матрицей размера
составленная из элементов Положение элементов в таблице определяется двойным индексом Если в матрице Квадратной матрицей называется матрица, в которой число строк совпадает с числом столбцов. Если элементы в квадратной матрице располагаются симметрично относительно главной диагонали, то такая матрица называется симметричной. Диагональной матрицей называется матрица, в которой все элементы, кроме стоящих на главной диагонали, равны 0. Единичная матрица, это диагональная матрица, у которой на главной диагонали стоят 0. Матричная алгебра это множество матриц плюс множество операций, которые можно выполнять над матрицами. В любой алгебре есть два замечательных числа – это ноль и единица. Ноль не изменяет число при сложении, единица не изменяет число при умножении, т.е.
В алгебре матриц также есть подобные элементы – это нулевая матрица, она играет роль нуля в алгебре матриц и это единичная матрица соответствующей размерности, она играет роль единицы в алгебре матриц.
Сложение матриц. Складывать можно только матрицы, имеющие одинаковую размерность. Сложением двух матриц называется операция, при которой складываются элементы, стоящие на одинаковых местах в соответствующих таблицах. Пример:
Умножение матрицы на число. Для того чтобы умножить матрицу на число Пример:
Умножение матриц. Умножение матриц в алгебре матриц не коммутативно. Для того, чтобы произведение матриц существовало необходимо чтобы число столбцов первой матрицы равнялось числу строк второй матрицы. Если матрица
Так как произведение матриц не коммутативно, следует различать умножение матрицы Пример:
|
||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 696; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.5.180 (0.008 с.) |

 , образованное парой вещественных чисел
, образованное парой вещественных чисел  , взятых в определенном порядке. Такое число
, взятых в определенном порядке. Такое число 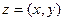 называется комплексным. Вещественные числа
называется комплексным. Вещественные числа 

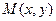 ; эту точку также называют изображением комплексного числа и обратно, пару чисел
; эту точку также называют изображением комплексного числа и обратно, пару чисел  , образующих комплексное число
, образующих комплексное число  .
.
 - модуль комплексного числа
- модуль комплексного числа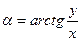 - аргумент комплексного числа
- аргумент комплексного числа является линейной функцией времени
является линейной функцией времени  , т.е.
, т.е.  , то
, то

 аналогично представлению синусоидального тока вращающимся вектором.
аналогично представлению синусоидального тока вращающимся вектором. , у которой модуль и аргумент равны соответственно амплитуде и аргументу синусоидального тока, называется комплексным мгновенным синусоидальным током.
, у которой модуль и аргумент равны соответственно амплитуде и аргументу синусоидального тока, называется комплексным мгновенным синусоидальным током. считаются равными, если совпадают изображающие их точки. Это означает, что равенство
считаются равными, если совпадают изображающие их точки. Это означает, что равенство  имеет место в том, и только в том случае, когда
имеет место в том, и только в том случае, когда ,
,  .
. .
. и помня, что
и помня, что  .
.

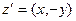 называется комплексно сопряженным к числу
называется комплексно сопряженным к числу 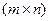 называется прямоугольная таблица
называется прямоугольная таблица ,
, и содержащая
и содержащая  строк и
строк и 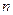 столбцов.
столбцов. , первый означает номер строки, второй номер столбца на пересечении которых стоит данный элемент. Запись группы величин в виде матрицы не предусматривает каких-либо действий над ними. Это лишь одна из форм упорядоченной записи в виде условной таблицы.
, первый означает номер строки, второй номер столбца на пересечении которых стоит данный элемент. Запись группы величин в виде матрицы не предусматривает каких-либо действий над ними. Это лишь одна из форм упорядоченной записи в виде условной таблицы.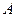 строки сделать столбцами, а столбцы строками, то получается транспонированная матрица
строки сделать столбцами, а столбцы строками, то получается транспонированная матрица  .
. .
.
 , необходимо каждый элемент этой матрицы умножить на число
, необходимо каждый элемент этой матрицы умножить на число 
 , а матрица
, а матрица  размерность
размерность  , то матрица
, то матрица  имеет размерность
имеет размерность  . В качестве элементов расположенных на пересечении
. В качестве элементов расположенных на пересечении 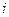 -той строки и
-той строки и