
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямоугольная декартова система координат на плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Прямоугольная декартова система координат на плоскости. Введем прямоугольную систему координат на плоскости. Для этого проведем на плоскости две взаимно перпендикулярные прямые, выберем на каждой из них положительное направление, указав его стрелочкой, и выберем на каждой из них масштаб (единицу измерения длины). Обозначим точку пересечения этих прямых буквой О и будем считать ее началом отсчета. Так мы получили прямоугольную систему координат на плоскости. Каждую из прямых с выбранным началом отсчета О, направлением и масштабом называют координатной прямой или координатной осью. Прямоугольную систему координат на плоскости обычно обозначают Oxy, где Ox и Oy – ее координатные оси. Ось Ox называют осью абсцисс, а ось Oy – осью ординат. Уравнение окружности радиуса R с центром в точке О (х 0, у 0) имеет вид:
(х – х 0) 2 + (у – у 0) 2 = R 2.
Опр.: Множество упорядоченных троек чисел в избранной системе координат называется трехмерным пространством.
Всякое уравнение первой степени с двумя переменными x и y вида Уравнение Теорема. Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и вторая прямая перпендикулярна к плоскости. Теорема. Для перпендикулярности прямой a и плоскости Уравнение прямой, проходящей через две заданные точки на плоскости.
Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.
Теорема. Всякое уравнение вида
Если все коэффициенты А, В, С и D в общем уравнении плоскости
Общее уравнение плоскости вида Определение. Две плоскости называются параллельными, если они не имеют общих точек. Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны. Если одна из двух параллельных плоскостей параллельна третьей плоскости, то другая плоскость либо тоже параллельна этой плоскости, либо совпадает с ней. Теорема. Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны. Для параллельности плоскостей Для параллельности двух несовпадающих плоскостей Теорема. Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и вторая прямая перпендикулярна к плоскости. Теорема. Для перпендикулярности прямой a и плоскости А) Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы. ЕСЛИ НАБОР ВЕКТОРОВ СОДЕР. НУЛ.ВЕКТОР ХОТЯ БЫ 2 РАВН.ВЕКТОРА Ранг матрицы Определение Рангом матрицы Обозначается На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду. Элементарные преобразования над строками (столбцами) матрицы не меняют её ранга. Ранг ступенчатой матрицы равен количеству её ненулевых строк.
Сначала дадим определение определителя квадратной матрицы порядка n на n как сумму произведений перестановок элементов матрицы. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равны) Определитель матрицы А обозначается как: det(A), |A| или ∆(A). Определитель матрицы А есть число, равное На основании озвученного определения справедливы следующие свойства определителя матрицы. 1. Определитель матрицы А равен определителю транспонированной матрицы АТ, то есть, 2. Если в квадратной матрице все элементы хотя бы одной из строк (одного из столбцов) нулевые, определитель такой матрицы равен нулю.
3. Если переставить местами две любые строки (столбца) в квадратной матрице, то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак).
4. Если в квадратной матрице хотя бы две строки (два столбца) одинаковы, то ее определитель равен нулю.
5. Если в квадратной матрице все элементы какой-либо строки (столбца) умножить на некоторое число k, то определитель полученной матицы будет равен определителю исходной матрицы, умноженному на k. Например,
6. Если все элементы какой-либо строки (столбца) квадратной матрицы представляют собой сумму s слагаемых (s – натуральное число, большее единицы), то определитель такой матрицы будет равен сумме s определителей матриц, полученных из исходной, если в качестве элементов строки (столбца) оставить по одному слагаемому. Например,
7. Если к элементам некоторой строки (столбца) матрицы прибавить соответствующие элементы другой строки (столбца), умноженные на произвольное число k, то определитель полученной матрицы будет равен определителю исходной матрицы.
8. Определитель квадратной матрицы
9. Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.
10. Определитель произведения квадратных матриц одного порядка равен произведению их определителей, то есть,
Рассмотрим квадратную матрицу A n -го порядка.
Алгебраическое дополнение Ai , j элемента ai j определяется формулой
Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:
Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:
Рассмотрим квадратную матрицу
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля
формулы для нахождения неизвестных переменных по методу Крамера Прямоугольная декартова система координат на плоскости. Введем прямоугольную систему координат на плоскости. Для этого проведем на плоскости две взаимно перпендикулярные прямые, выберем на каждой из них положительное направление, указав его стрелочкой, и выберем на каждой из них масштаб (единицу измерения длины). Обозначим точку пересечения этих прямых буквой О и будем считать ее началом отсчета. Так мы получили прямоугольную систему координат на плоскости. Каждую из прямых с выбранным началом отсчета О, направлением и масштабом называют координатной прямой или координатной осью. Прямоугольную систему координат на плоскости обычно обозначают Oxy, где Ox и Oy – ее координатные оси. Ось Ox называют осью абсцисс, а ось Oy – осью ординат. Уравнение окружности радиуса R с центром в точке О (х 0, у 0) имеет вид:
(х – х 0) 2 + (у – у 0) 2 = R 2.
Опр.: Множество упорядоченных троек чисел в избранной системе координат называется трехмерным пространством.
Всякое уравнение первой степени с двумя переменными x и y вида Уравнение Теорема. Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и вторая прямая перпендикулярна к плоскости. Теорема. Для перпендикулярности прямой a и плоскости
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 554; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |




 , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида
, где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида  необходимо и достаточно, чтобынаправляющий вектор прямой a и нормальный вектор плоскости
необходимо и достаточно, чтобынаправляющий вектор прямой a и нормальный вектор плоскости 
 .
. , где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида
, где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида  равна единице, то есть,
равна единице, то есть, 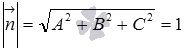 , и
, и  .
. и
и 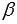 необходимо и достаточно, чтобы система линейных уравнений вида
необходимо и достаточно, чтобы система линейных уравнений вида  не имела решений (была несовместна).
не имела решений (была несовместна). называется ранг её системы строк или столбцов.
называется ранг её системы строк или столбцов.
 .
. .
. равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
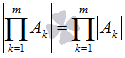 , где m – натуральное число большее единицы, Ak, k=1,2,…,m – квадратные матрицы одного порядка.
, где m – натуральное число большее единицы, Ak, k=1,2,…,m – квадратные матрицы одного порядка. .
. .
. .
. .
.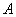 . Обратную матрицу
. Обратную матрицу можно найти по следующей формуле:
можно найти по следующей формуле: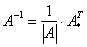 , где
, где  – определитель матрицы
– определитель матрицы 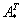 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
.


