
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Хотя бы 2 век. С пропорц. КоордСодержание книги
Поиск на нашем сайте
4.СОДЕРЖИТ ВЕКТОР.БОЛЬШЕ,ЧЕМ РАЗМЕРНОСТЬ ПРОСТР.
В линейной алгебре линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу. Критерий зависимости-независимости векторов. Если ранг матрицы,составленной из компонентов вех векторов системы равен числу векторов,то данная сист.вект.линейно независима,если же ранг этой матрицы меньше числа векторов,то сист. Линейно зависима Б) Рангом системы векторов называется максимальное число линейно независимых векторов системы.(и равен рангу матрицы, составленной из координат концов этих векторов) Число r называется рангом матрицы,если выполняются условия: 1)среди миноров порядка r есть по крайней мере один отличный от нуля 2)все миноры порядка большего чем r,матрицы А либо равны нулю, либо не могут быть составлены В) Теорема Кронекера-Капелли — критерий совместности системы линейных алгебраических уравнений.
Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины стробцов. aij - элемент матрицы, который находится в i -ой строке и j -м столбце. Таблица берется либо в круглые скобки, либо окружается двумя параллельными вертикальными прямыми. Некоторые операции над матрицами, такие как сложение и вычитание, допускаются только для матриц одинакового размера. Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число. Суммой матриц и одного размера называется матрица такого же размера, получаемая из исходных путем сложения соответствующих элементов.
Операции умножение матрицы на число и сумма матриц называются линейными. Произведением матрицы на матрицу называется матрица такая, что элемент матрицы, стоящий в -ой строке и -ом столбце, т.е. элемент, равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -ого столбца матрицы. Определение. Сумма двух матриц
Операция умножения матрицы на число определена ДЛЯ МАТРИЦ ЛЮБОГО ПОРЯДКА. Определение. Произведение матрицы
Операция умножения двух матриц А и В определяется только для случая, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В. Определение. Произведение матрицы А порядка
Единичная матрица - это диагональная матрица, у которой каждый элемент на главной диагонали равен единице. Определение. Матрица Определение. Минор k-ого порядка матрицы A порядка m на n – это определитель матрицы порядка k на k, которая получается из элементов матрицы А, находящихся в выбранных k строках и k столбцах. (k не превосходит наименьшего из чисел m или n). Определение. Алгебраическим дополнением элемента
Составим алгоритм нахождения обратной матрицы с использованием равенства 1. Вычисляем определитель матрицы А и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима). 2. Строим 3. Транспонируем матрицу 4. Умножаем каждый элемент матрицы
5. Проводим проверку результата, вычисляя произведения
Рангом системы строк называется максимальное количество линейно независимых строк этой системы. Строчный ранг матрицы равен её столбцовому рангу. Ранг матрицы Определение Рангом матрицы Обозначается На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду. Элементарные преобразования над строками (столбцами) матрицы не меняют её ранга. Ранг ступенчатой матрицы равен количеству её ненулевых строк.
Сначала дадим определение определителя квадратной матрицы порядка n на n как сумму произведений перестановок элементов матрицы. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равны) Определитель матрицы А обозначается как: det(A), |A| или ∆(A). Определитель матрицы А есть число, равное На основании озвученного определения справедливы следующие свойства определителя матрицы. 1. Определитель матрицы А равен определителю транспонированной матрицы АТ, то есть, 2. Если в квадратной матрице все элементы хотя бы одной из строк (одного из столбцов) нулевые, определитель такой матрицы равен нулю.
3. Если переставить местами две любые строки (столбца) в квадратной матрице, то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак).
4. Если в квадратной матрице хотя бы две строки (два столбца) одинаковы, то ее определитель равен нулю.
5. Если в квадратной матрице все элементы какой-либо строки (столбца) умножить на некоторое число k, то определитель полученной матицы будет равен определителю исходной матрицы, умноженному на k. Например,
6. Если все элементы какой-либо строки (столбца) квадратной матрицы представляют собой сумму s слагаемых (s – натуральное число, большее единицы), то определитель такой матрицы будет равен сумме s определителей матриц, полученных из исходной, если в качестве элементов строки (столбца) оставить по одному слагаемому. Например,
7. Если к элементам некоторой строки (столбца) матрицы прибавить соответствующие элементы другой строки (столбца), умноженные на произвольное число k, то определитель полученной матрицы будет равен определителю исходной матрицы.
8. Определитель квадратной матрицы
9. Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.
10. Определитель произведения квадратных матриц одного порядка равен произведению их определителей, то есть,
Рассмотрим квадратную матрицу A n -го порядка.
Алгебраическое дополнение Ai , j элемента ai j определяется формулой
Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:
Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:
Рассмотрим квадратную матрицу
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля
формулы для нахождения неизвестных переменных по методу Крамера
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.222.106 (0.011 с.) |

 и
и  - это матрица, элементы которой равны сумме соответствующих элементов матриц А и В, то есть,
- это матрица, элементы которой равны сумме соответствующих элементов матриц А и В, то есть,  .
.
 - это матрица, элементы которой получаются умножением соответствующих элементов исходной матрицы на число
- это матрица, элементы которой получаются умножением соответствующих элементов исходной матрицы на число  .
.
 и матрицы В порядка
и матрицы В порядка  - это такая матрица С порядка
- это такая матрица С порядка  , каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть,
, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть,

 называется обратной для матрицы
называется обратной для матрицы  , определитель которой отличен от нуля
, определитель которой отличен от нуля  , если справедливы равенства
, если справедливы равенства  , где E – единичная матрица порядка n на n.
, где E – единичная матрица порядка n на n. квадратной матрицы
квадратной матрицы  .
. .
. - матрицу из алгебраических дополнений элементов
- матрицу из алгебраических дополнений элементов  .
. . Этой операцией завершается нахождение обратной матрицы
. Этой операцией завершается нахождение обратной матрицы  и
и  . Если
. Если 

 называется ранг её системы строк или столбцов.
называется ранг её системы строк или столбцов.
 .
. .
. равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
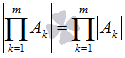 , где m – натуральное число большее единицы, Ak, k=1,2,…,m – квадратные матрицы одного порядка.
, где m – натуральное число большее единицы, Ak, k=1,2,…,m – квадратные матрицы одного порядка. .
. .
. .
. .
.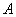 . Обратную матрицу
. Обратную матрицу можно найти по следующей формуле:
можно найти по следующей формуле: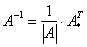 , где
, где  – определитель матрицы
– определитель матрицы 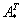 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
.


