
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декартова система координат плоскости и пространстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть О - произвольная фиксированная точка некоторой плоскости и (
Опр.20 Совокупность фиксированной точки О и ортонормированного базиса (
Легко увидеть, что декартова система координат на плоскости задается двумя взаимно перпендикулярными прямыми - осями, на каждой из которых выбрано положительное направление и задан отрезок единичной длины. Оси координат делят плоскость на четыре области – четверти или квадранты. Четверти нумеруются против часовой стрелки, как на рис.13.
Рассмотрим произвольную точку М плоскости Oxу (Рис.13). Радиус-вектором точки М по отношению к точке О называется вектор Координатами точки М в системе координат O Координаты точки могут быть найдены как проекции радиус-вектора на каждую из осей, х= ах=Прох
Обратно: если М(х; у), то
Как и на плоскости, точка О называется началом координат. Прямые Ох, Оу и Оz, проходящие через начало координат в направлении базисных векторов Ox – ось абсцисс, Оу – ось ординат, Oz – ось аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями. Они делят пространство на восемь областей - октантов. Координатами точки М называются координаты радиус-вектора Обратно: если М(х; у; z), то
Прямоугольная система координат в пространстве дает возможность установить взаимно однозначное соответствие между точками пространства и упорядоченными тройками чисел (их координатами), а на плоскости - между точками плоскости и упорядоченными парами чисел. В декартовой системе координат упорядоченная пара чисел одновременно задает как точку данной плоскости, так и радиус-вектор этой точки и целое множество равных ему векторов. Аналогично и в трёхмерном случае. В дальнейшем будем задавать векторы не двумя точками (начальной и конечной) а только конечной с указанием её координат. Считаем начальной точкой всех векторов (если противное не оговорено отдельно) точку О – начало координат.
Аналогично рассмотренным случаям n=2 и n=3 можно ввести понятие декартовой системы координат n-мерного пространства, которое можно обозначить R n. Точки такого пространства, как и векторы, задаются указанием упорядоченного набора n чисел
|
|||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 839; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

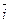 ;
; 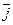 ) - один из ортонормированных базисов той же плоскости.
) - один из ортонормированных базисов той же плоскости.
 , соединяющий начало координат с данной точкой.
, соединяющий начало координат с данной точкой. в базисе (
в базисе ( =(ах; ау).
=(ах; ау). Опр.21 Совокупность фиксированной точки О и ортонормированного базиса (
Опр.21 Совокупность фиксированной точки О и ортонормированного базиса ( ) называется декартовой (или прямоугольной) системой координат в пространстве размерности n=3.
) называется декартовой (или прямоугольной) системой координат в пространстве размерности n=3. - её декартовых координат.
- её декартовых координат.


