
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства скалярного произведенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
5.2.1 Свойство коммутативности: Это вытекает непосредственно из определения скалярного произведения; 5.2.2 Числовой множитель можно выносить за знак скалярного произведения, т. е. (l
Доказательство этого свойства рекомендуем провести самостоятельно; 5.2.3 Свойство дистрибутивности Учитывая, что прa(
При 5.2.4 Скалярный квадрат вектора т. е. Действительно, 5.2.5 Скалярное произведение двух ненулевых векторов тогда и только тогда, когда
откуда j=90°, т.е. 5.2.6 Косинус угла между ненулевыми векторами по формуле В самом деле, если равенства можно выразить cos(j).
Пример 4 Для базисных векторов ( Найти 1) Модуль вектора 2) Скалярное произведение 3) Угол между векторами
Решение: 1) Воспользуемся тем, что |
= 2 +(-3 = 4 = 4 = 4 Вычислим каждое скалярное произведение по определению:
=4+0– 24+9– 36+144=97. Модуль вектора | 2) = 2 +(-3 = 2 = 2
= 2 =2×1 –3×0 +5×2 –2×9+10×6– 12×16=2– 0+10– 18+60– 192= -138. Получили Знак “ – “показывает, что угол между векторами 3) Угол между векторами можно найти по его косинусу, Выше найдено |
= +4 = = = =1 – 4×0 +8×2 +4×9 +16×16=1– 0+16+36+256=307, получили
(
Ответ: | Декартов базис и декартова система координат Декартов базис Опр.20 Векторы произведение любой пары различных векторов равно нулю. Условие ортогональности можно заменить попарной перпендикулярностью этих векторов
Опр.21 Векторы из векторов единичный.
Опр.22 Векторы ортогональны и нормированы. Условие ортонормированности векторов в терминах скалярного произведения можно записать следующим образом: (7) Опр.23 Декартовым базисом векторного пространства называются векторы
является размерностью векторного пространства.
Декартовым базисом на плоскости можно взять два вектора, которые единичные и взаимно перпендикулярные. Такие векторы обозначают Разложение вектора
Например, разложение вектора Декартовым базисом трёхмерного пространства можно взять три вектора (
Разложение вектора Например, разложение вектора
|
||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.78.107 (0.011 с.) |

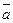 ×
× 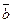 =
=  )=
)=  , имеем
, имеем ;
; .
. Если
Если  Обратно, если
Обратно, если  (7)
(7)  .
. ;
;  ;
;  ) известно, что |
) известно, что |  , если
, если  )×(2
)×(2  ;
;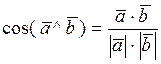 .
. .
. ,
, 1430.
1430. называется ортогональными, если скалярное
называется ортогональными, если скалярное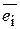 ^
^  ,
,  .
. .
.  и
и 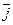 , их порядок фиксирован:
, их порядок фиксирован:  =
= 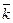 , их порядок фиксирован:
, их порядок фиксирован: 


