
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
тригонометрической и показательной формахСодержание книги
Поиск на нашем сайте
Пусть даны комплексныt числа В показательной и тригонометрической формах записи их можно сравнивать, умножать на число, сопрягать, перемножать, делить, возводить в степень и извлекать из них корни. Рассмотрим эти действия подробнее.
11.3.1 Два комплексных числа равны, когда их модули равны и аргументы отличаются на число, кратное
В противном случае комплексные числа различные; 11.3.2 При умножении комплексного числа на действительное число
11.3.3 При сопряжении комплексного числа получится число с тем же модулем, но с аргументом противоположного знака,
т.е его модуль не меняется, а аргумент изменит знак (либо вычитается из 11.3.4 При умножении числа комплексного числа
т.е. при умножении двух комплексных чисел их модули перемножаются а аргументы складываются;
11.3.5 При делении числа
т.е. при делении двух комплексных чисел их модули делятся а аргументы вычитаются;
11.3.6 При возведении в натуральную степень n комплексного числа получается комплексное число, модуль которого является n –й степенью модуля числа z и аргумент получается умножением аргумента числа z на натуральное число n,
(23) 11.3.7 При извлечении корня степени получается множество комплексных чисел, модули которых являются корнем степени n из модуля числа z, аргумент каждого получается подстановкой целого числа k в выражение
(24) – Формула Муавра – Лапласа. Среди корней степени
Пример 15 Даны комплексные числа Найти модули и аргументы чисел Найти и изобразить на комплексной плоскости все корни уравнения Решение: 1) Для числа
Тогда
2)
3)
4)
5)
Подставим последовательно к =0, к =1, к =2:
Изобразим найденные решения уравнения все три найденных решения лежат на окружности с центром в начале координат и радиусом
Упражнения 12.1 В треугольнике АВС проведена медиана AD, D – середина стороны ВС. Доказать, что 12.2 Дан параллелепипед ABCDA1B1C1D1 , найти суммы векторов: 1) 3) Ответ:1) 12.3 Дан тетраэдр ABCD. Найти суммы векторов: 1) Ответ:1) 12.4 Даны три компланарных единичных вектора вектора причем Построить вектор Ответ:
12.5 Составляющие для скорости направлены под углом 60 0 друг к другу и равны соответственно 6 и 4 м/с. Найти скорость результирующего движения. Ответ:
12.6 В параллелограмме ABCD диагоналей. Выразить векторы Ответ:
12.7 Найти скалярное произведение векторов, модули которых 5 и 6 и угол между ними равен 1) 45 0; 2) 60 0; 3) 90 0; 4) 120 0; 5) 180 0. Ответ: 1) 15
12.8 Дано 1) 3) 5) Ответ: 1)-10; 2) 25; 3) -39; 4) 61; 5) 1101.
12.9 Дано Ответ:
12.10 Даны три некомпланарных вектора
Найти 1) Ответ: 1) -3; 2) 26.
12.11 Определить длины диагоналей параллелограмма, построенного на векторах угол между которыми равен 60 0. Ответ: 3 и
12.12 Найти скалярное произведение векторов 1) 2) 3) Ответ: 1) 5; 2) -3; 3) -16.
12.13 При каком значении m векторы перпендикулярны? Ответ: -7.
12.14 Найти площадь треугольника АВС, если А(1; 2: 3), В(-1; 3; 1) и С(0; -1; 4). Ответ:
12.14 Найти объем тетраэдра АBCD, если его вершины A(1; 2; 1), B(3; -1; 2), C(0; 5; -4) и D(5; 1; 1). Ответ: 13,5.
12.15 Записать полярные координаты точек А(0; 3), В(-5; 0), С(2; -4). Ответ: А(3; 0), В(5;
12.16 Найти решения уравнения
Ответ: z1=-1, z2=1, z3= – 2 i, z4=2 i.
12.17 Изобразить на комплексной плоскости решения уравнения
Ответ:
Вопросы для самоконтроля 13.1 В чём разница между скалярными и векторными величины? Привести насколько примеров величин обоих видов. 13.2 Перечислите способы построения суммы векторов, чем они отличаются и могут ли получиться разные результаты для одинаковых слагаемых. 13.3 Как построить разность двух векторов, как связана разность векторов с суммой таких векторов? 13.4 Перечислить свойства линейных операций над векторами (сложения, вычитания, умножения на число). 13.5 Будут ли линейно зависимыми противоположные векторы? 13.6 Можно ли взять базисом два ненулевых вектора с углом между ними 600? 13.7 Какие векторы задают аффинные координаты (-1; 0), (0; 1), (0; -1)? 13.8 Что можно сказать о взаимном расположении двух векторов, скалярное произведение которых нулевое, отрицательное, положительное? 13.9 Как найти модуль вектора, заданного своим разложением по аффинному базису с известными модулями базисных векторов и углами между ними? 13.10 Как графически найти координаты точки пространства после введения декартовой системы координат этого пространства? 13.11 Как сложить, вычесть два вектора декартовых координатах и умножить их на число? Перечислить свойства этих операций. 13.12 Перечислить способы нахождения результатов скалярного и векторного произведений двух векторов, заданных координатами. Чем существенно отличаются такие результаты? 13.13 Как разделить отрезок, заданный координатами начала и конца в отношении 3:2? 13.14 Перечислить последовательность действий для нахождения площади треугольника, заданного координатами вершин в пространстве. 13.15 Перечислить способ вычисления смешанного произведения трёх векторов и его основные свойства с геометрическим смыслом. 13.16 Как проверить некомпланарность трёх векторов с известными координатами? 13.17 Как найти координаты вектора в аффинном базисе, заданном своими координатами в декартовом базисе? 13.18 Что необходимо задать, чтобы получить полярную систему координат на фиксированной плоскости? Что и как нужно будет измерять, чтобы получать полярные координаты точек плоскости? 13.19 Указать связь между декартовыми и полярными координатами точек плоскости. Каково должно быть взаимное расположение декартовой и полярной систем координат при этом? 14.20 Как перевести комплексное число из алгебраической формы записи в тригонометрическую и показательную. Как выполнить обратное преобразование? 14.21 Записать формулы возведения в степень и извлечения корня из комплексного числа.
14 Контрольное задание
14.1 В базисе заданы векторы Найти
14.2 Даны векторы Найти для них
2) 3) Косинусы углов и углы между
4) 5) Площадь треугольника построенного на векторах 6) Смешанное произведение 7) Объём пирамиды построенной на 8) Разложение вектора
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.180.147 (0.009 с.) |

 ,
,  ,
,  .
. .
.
 получается число, модуль которого равен |
получается число, модуль которого равен |  ,
,

 на число
на число  получается число, модуль которого получается умножением модуля числа
получается число, модуль которого получается умножением модуля числа 
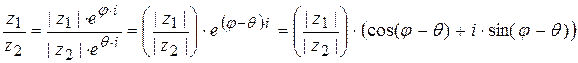 ,
,
 - Формула Муавра;
- Формула Муавра; , из комплексного числа
, из комплексного числа ,
, ,
,
 с центром в начале координат и являются вершинами вписанного в такую окружность правильного n - угольника с поворотом начальной вершины на угол
с центром в начале координат и являются вершинами вписанного в такую окружность правильного n - угольника с поворотом начальной вершины на угол  (при к =0), остальные получаются каждый раз поворотом на угол
(при к =0), остальные получаются каждый раз поворотом на угол  .
. ,
,  и
и  .
. .
. .
. ,
,  ,
,  .
. ,
, ;
; .
.
 ;
;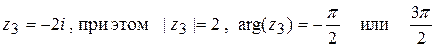 .
.

 ;
; .
. .
.
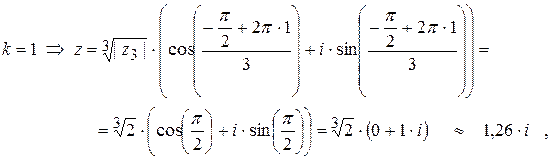

 . Три соответствующих точки комплексной плоскости являются вершинами правильного треугольника с поворотом начальной вершины на угол
. Три соответствующих точки комплексной плоскости являются вершинами правильного треугольника с поворотом начальной вершины на угол 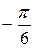 , угол между ними
, угол между ними  или 1200.
или 1200.
 .
. ; 2)
; 2)  ;
; ; 4)
; 4)  .
. ; 2)
; 2) 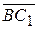 ; 3)
; 3)  ; 4)
; 4)  .
. ; 2)
; 2)  .
.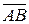 ; 2)
; 2)  .
. ,
, .
. и вычислить его модуль.
и вычислить его модуль. .
. м/с.
м/с.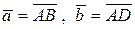 , О – точка пересечения
, О – точка пересечения через векторы
через векторы  и
и  .
. .
. ; 2) 15; 3) 0; 4) -15; 5) -30.
; 2) 15; 3) 0; 4) -15; 5) -30. 0.
0. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; .
. . Найти модуль вектора
. Найти модуль вектора  .
. .
. , причем известно, что
, причем известно, что ,
,  .
. ; 2)
; 2)  .
. и
и  , где
, где  и
и  – единичные векторы,
– единичные векторы, и
и  ;
;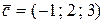 и
и  ;
; , если А(1; 2; 0), В(0; -1; 3), С(4; -1; 3) и D(2; 0; -2).
, если А(1; 2; 0), В(0; -1; 3), С(4; -1; 3) и D(2; 0; -2). .
. ).
). .
. .
.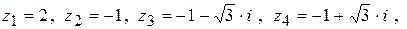


 с модулями
с модулями  и углом между ними
и углом между ними 
 .
.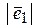


 4
4
 7
7
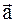 =2
=2  -3
-3 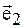
 =5
=5 
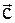 ,
, 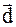 (см. таблицу).
(см. таблицу).






 по векторам
по векторам  , если они образуют базис.
, если они образуют базис.


