Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямоугольная система координат.Содержание книги
Поиск на нашем сайте
ЛЕКЦИИ ПО ВЫСШЕЙ МАТЕМАТИКЕ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Новосибирск 2005 СОДЕРЖАНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ. В математике первичными понятиями являются понятия множества, элемента и принадлежности элемента множеству. Множество — это совокупность элементов, объединенных общим (характеристическим) свойством. Обозначения: A, B, C,¼, X, Y, Z — множества; a, b, c,¼, x, y, z — элементы множеств; x Î A обозначает принадлежность элемента х множеству А; x Ï A — x не принадлежит множеству А; Þ — следовательно, если ¼ то; Û — тогда и только тогда, необходимо и достаточно; "— любой, каждый; $ — существует. Способы задания множеств. — Перечислением элементов. Например, Х = {1, 2} — множество Х состоит из двух элементов: 1 и 2. — Указанием характеристического свойства.
Например, X ={ x: (x -1)(x +3) = 0} — это множество содержит два элемента — корни уравнения (x -1)(x +3) = 0, то есть числа 1 и -3. А ={(l1, …, ln): l12 + l22 + … + ln2 = 0} — такое множество содержит единственный набор чисел, состоящий из n нулей, т. е. А ={(0, 0, …, 0)}. Введем понятия пустого множества Æ и универсального множества U. Пустое множество – это множество, не содержащее ни одного элемента: " х х Ï Æ. Универсальное множество – это множество, содержащее все элементы: " х х Î U. Например { x Î R: x 2 < 0} = Æ. { x Î R: x 2 ³ 0} = R = U. Во втором примере множество вещественных чисел R играет роль универсального множества. Рассмотрим понятия подмножества и равенства множеств. Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В: А Ì В Û (х Î А Þ х Î В) Очевидно, что Æ Ì А, А Ì А, А Ì U для любого множества А. Множества А и В называются равными, если каждый элемент множества А является элементом множества В и, наоборот, каждый элемент множества В является элементом множества А: А = В Û А Ì В и В Ì А. 2. Операции над множествами. Объединением А È В двух множеств А и В называется множество, состоящее из элементов, содержащихся либо в А, либо в В.
x Î A È B Û x Î A или x Î B; x Ï A È B Û x Ï A и x Ï B. Пересечением А Ç В двух множеств А и В называется множество, состоящее из элементов, содержащихся и в А, и в В. x Î A Ç B Û x Î A и x Î B; x Ï A Ç B Û x Ï A или x Ï B. Разностью А \ В множеств А и В называется множество, состоящее из тех элементов множества А, которые не принадлежат множеству В. x Î A \ B Û xÎ A и x Ï B; x Ï A \ B Û x Ï A или x Î B. Разность U \ A называется дополнением множества А и обозначается x Î Свойства операций. 1. A È B = B È A 8. 2. A Ç B = B Ç A 9. A \ B = A Ç 3. A È(B È C)=(A È B)È C 10. A È A = A Ç A = A 4. A Ç (B Ç C)=(A Ç B)Ç C 11. A ÈÆ= A; A ÇÆ=Æ 5. A È(B Ç C)=(A È B)Ç(A È C) 12. A È U = U; A Ç U = A 6. A Ç (B È C)=(A Ç B)È(A Ç C) 13. A È 7. Доказательство свойства 6. A Ç (B È C)=(A Ç B)È(A Ç C). Возьмем x Î A Ç(B È C)Þ x Î A и x Î B È C Þ x Î A и (x Î B или x Î C) Þ (x Î A и x Î B) или (x Î A и x Î C) Þ x Î A Ç B или x Î A Ç C)Þ x Î(A Ç B)È(A Ç C).
Доказано, что. A Ç (B È C) Ì (A Ç B)È(A Ç C). Возьмем x Î(AÇ B)È(A Ç C) Þ x Î A Ç B или x Î A Ç C Þ (xÎ A и x Î B) или (x Î A и x Î C) Þ xÎ A и (x Î B или x Î C) Þ x Î A и x Î B È C Þ x Î A Ç(B È C). Доказано, что A Ç (B È C) É (A Ç B)È(A Ç C). Тождество доказано. Доказательство свойства 13. A È A È A È Докажем, что A È Возьмем х Î U Þ x Î A или х Ï А Þ x Î A или х Î A Ç Доказательство. Предположим противное, что A Ç Остальные свойства предлагается доказать самостоятельно в качестве упражнений.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ ВЕКТОРНАЯ АЛГЕБРА ОПЕРАЦИИ НАД ВЕКТОРАМИ. Векторы на плоскости и в пространстве можно складывать и умножать на числа. Сложение векторов производится по правилу параллелограмма: если привести векторы к общему началу, то их суммой будет вектор, имеющий то же начало и являющийся диагональю параллелограмма, построенного на данных векторах. Произведением вектора Операции над векторами удовлетворяют следующим свойствам:
l (m (l + m) l ( Если векторы
ПРЯМАЯ НА ПЛОСКОСТИ ЛИНИИ НА ПЛОСКОСТИ. Линия на плоскости может быть задана уравнением от двух переменных F (x, y) = 0, которому удовлетворяют координаты каждой точки этой линии и не удовлетворяют координаты ни одной другой точки. Для нахождения точек пересечения двух линий надо найти решения системы уравнений этих линий. Линия на плоскости, а также в пространстве, может рассматриваться как траектория движения точки. В этом случае ее описывают системой параметрических уравнений ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ. Пусть даны точка М 0 (x 0, y 0) и вектор
Возьмем на искомой прямой произвольную точку М и рассмотрим Полученное уравнение называется векторным уравнением прямой. Переписав это уравнение в координатной форме, получим уравнение прямой, проходящей через точку перпендикулярно вектору: A (x – x 0) + B (y – y 0 ) = 0. В полученном уравнении x 0 и y 0 — координаты точки М 0, а A и В — координаты вектора
Раскрыв скобки в полученном уравнении и обозначив число – A x 0 – B y 0 через С, получим общее уравнение прямой: A x + B y + С = 0. В этом уравнении коэффициенты А и В при переменных являются координатами вектора нормали. Если А = 0, то уравнение примет вид B y + С = 0, нормаль Прямые, заданные общими уравнениями будут параллельны, если их нормали коллинеарны, и перпендикулярны, если их нормали ортогональны: L 1: A 1 x + B 1 y + C 1 = 0, L 2: A 2 x + B 2 y + C 2 = 0, L 1 ÷÷ L 2 Û
УГОЛ МЕЖДУ ПРЯМЫМИ. Углом между прямыми называется острый угол между ними. Угол j между прямыми можно находить, используя направляющие векторы, векторы нормалей или угловые коэффициенты прямых. Пусть прямые L 1 и L 2 заданы своими каноническими уравнениями: L 1: L 2: Заметим, что угол между направляющими векторами равен либо углу j, либо смежному с ним тупому углу p-j, так как эти векторы направлены параллельно прямым. Поскольку cos (p-j) = - cos j, то cos j = êcos (p-j) ê. Следовательно, имеем cos j = ê Пусть прямые L 1 и L 2 заданы своими общими уравнениями: L 1: A 1 x + B 1 y + C 1 = 0, L 2: A 2 x + B 2 y + C 2 = 0, Заметим, что угол между векторами нормалей равен либо углу j, либо смежному с ним тупому углу p-j, так как эти векторы направлены перпендикулярно прямым. В результате получаем cos j = êcos (p-j) ê = ê Пусть теперь прямые L 1 и L 2 заданы уравнениями y = k 1 x + b 1 и y = k 2 x + b 2. Обозначим через a 1 и a 2 углы между прямыми L 1 и L 2 и осью ОХ. Тогда угол j между L 1 и L 2 равен j = a 1 – a 2 или j = a 2 – a 1. Следовательно, tg j = êtg (a 1 – a 2) ê=
ПЛОСКОСТЬ В ПРОСТРАНСТВЕ ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ. Пусть даны точка М 0 и вектор Возьмем на искомой плоскости произвольную точку М и рассмотрим Переписав это уравнение в координатной форме, получим уравнение плоскости, проходящей через точку перпендикулярно вектору:
A (x – x 0) + B (y – y 0 ) + C (z – z 0) = 0. В полученном уравнении x 0, y 0 и z 0 — координаты точки М 0, а А, В и С — координаты вектора Раскрыв скобки в полученном уравнении и обозначив число – A x 0 – B y 0 – С z 0 через D, получим общее уравнение плоскости: A x + B y + С z + D = 0. В этом уравнении коэффициенты А, В и С при переменных являются координатами вектора нормали. Если А = 0, то уравнение примет вид B y + С z + D = 0, нормаль Плоскости будут параллельны, если их нормали коллинеарны, и перпендикулярны, если их нормали ортогональны: P 1: A 1 x + B 1 y + C 1 z + D 1 = 0, P 2: A 2 x + B 2 y + C 2 z + D 2 = 0, P 1 ÷÷ P 2 Û
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ. Углом между плоскостями называется острый угол j между ними. Пусть плоскости P 1 и P 2 заданы уравнениями: P 1: A 1 x + B 1 y + C 1 z + D 1 = 0, P 2: A 2 x + B 2 y + C 2 z + D 2 = 0, Заметим, что угол между векторами нормалей равен либо углу j, либо смежному с ним тупому углу p-j, так как эти векторы направлены перпендикулярно плоскостям. В результате получаем cos j = êcos (p-j) ê = ê =
ПРЯМАЯ В ПРОСТРАНСТВЕ ПРЯМАЯ И ПЛОСКОСТЬ. Пусть даны плоскость P: A x + B y + С z + D = 0 с вектором нормали Получим условия параллельности и перпендикулярности прямой и плоскости. L êê P Û L ^ P Û Углом j между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. Заметим, что угол между нормалью к плоскости и направляющим вектором прямой будет равен = Точка пересечения прямой и плоскости находится как решение системы уравнений данных прямой и плоскости. При этом уравнения прямой лучше взять в параметрическом виде:
ПОЛУПРОСТРАНСТВА. Пусть имеется плоскость P: A x + B y + С z + D = 0 с вектором нормали Положительным полупространством, определяемым плоскостью P и ее нормалью
Таким образом, положительное полупространство задается неравенством A x + B y + С z + D ³ 0. Заметим, что выбор точки М 0 не влияет на полученный результат, поскольку равенство – A x 0 – B y 0 – C z 0 = D является верным для любой точки М 0 Î P. Отрицательным полупространством, определяемым плоскостью P и ее нормалью
Так как Таким образом, отрицательное полупространство задается неравенством A x + B y + С z + D £ 0.
ЛЕКЦИИ ПО ВЫСШЕЙ МАТЕМАТИКЕ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Новосибирск 2005 СОДЕРЖАНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ. В математике первичными понятиями являются понятия множества, элемента и принадлежности элемента множеству. Множество — это совокупность элементов, объединенных общим (характеристическим) свойством. Обозначения: A, B, C,¼, X, Y, Z — множества; a, b, c,¼, x, y, z — элементы множеств; x Î A обозначает принадлежность элемента х множеству А; x Ï A — x не принадлежит множеству А; Þ — следовательно, если ¼ то; Û — тогда и только тогда, необходимо и достаточно; "— любой, каждый; $ — существует. Способы задания множеств. — Перечислением элементов. Например, Х = {1, 2} — множество Х состоит из двух элементов: 1 и 2. — Указанием характеристического свойства. Например, X ={ x: (x -1)(x +3) = 0} — это множество содержит два элемента — корни уравнения (x -1)(x +3) = 0, то есть числа 1 и -3. А ={(l1, …, ln): l12 + l22 + … + ln2 = 0} — такое множество содержит единственный набор чисел, состоящий из n нулей, т. е. А ={(0, 0, …, 0)}. Введем понятия пустого множества Æ и универсального множества U. Пустое множество – это множество, не содержащее ни одного элемента: " х х Ï Æ. Универсальное множество – это множество, содержащее все элементы: " х х Î U. Например { x Î R: x 2 < 0} = Æ. { x Î R: x 2 ³ 0} = R = U. Во втором примере множество вещественных чисел R играет роль универсального множества. Рассмотрим понятия подмножества и равенства множеств. Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В: А Ì В Û (х Î А Þ х Î В) Очевидно, что Æ Ì А, А Ì А, А Ì U для любого множества А. Множества А и В называются равными, если каждый элемент множества А является элементом множества В и, наоборот, каждый элемент множества В является элементом множества А: А = В Û А Ì В и В Ì А. 2. Операции над множествами. Объединением А È В двух множеств А и В называется множество, состоящее из элементов, содержащихся либо в А, либо в В.
x Î A È B Û x Î A или x Î B; x Ï A È B Û x Ï A и x Ï B. Пересечением А Ç В двух множеств А и В называется множество, состоящее из элементов, содержащихся и в А, и в В. x Î A Ç B Û x Î A и x Î B; x Ï A Ç B Û x Ï A или x Ï B. Разностью А \ В множеств А и В называется множество, состоящее из тех элементов множества А, которые не принадлежат множеству В. x Î A \ B Û xÎ A и x Ï B; x Ï A \ B Û x Ï A или x Î B. Разность U \ A называется дополнением множества А и обозначается x Î Свойства операций. 1. A È B = B È A 8. 2. A Ç B = B Ç A 9. A \ B = A Ç 3. A È(B È C)=(A È B)È C 10. A È A = A Ç A = A 4. A Ç (B Ç C)=(A Ç B)Ç C 11. A ÈÆ= A; A ÇÆ=Æ 5. A È(B Ç C)=(A È B)Ç(A È C) 12. A È U = U; A Ç U = A 6. A Ç (B È C)=(A Ç B)È(A Ç C) 13. A È 7. Доказательство свойства 6. A Ç (B È C)=(A Ç B)È(A Ç C). Возьмем x Î A Ç(B È C)Þ x Î A и x Î B È C Þ x Î A и (x Î B или x Î C) Þ (x Î A и x Î B) или (x Î A и x Î C) Þ x Î A Ç B или x Î A Ç C)Þ x Î(A Ç B)È(A Ç C). Доказано, что. A Ç (B È C) Ì (A Ç B)È(A Ç C). Возьмем x Î(AÇ B)È(A Ç C) Þ x Î A Ç B или x Î A Ç C Þ (xÎ A и x Î B) или (x Î A и x Î C) Þ xÎ A и (x Î B или x Î C) Þ x Î A и x Î B È C Þ x Î A Ç(B È C). Доказано, что A Ç (B È C) É (A Ç B)È(A Ç C). Тождество доказано. Доказательство свойства 13. A È A È A È Докажем, что A È Возьмем х Î U Þ x Î A или х Ï А Þ x Î A или х Î A Ç Доказательство. Предположим противное, что A Ç Остальные свойства предлагается доказать самостоятельно в качестве упражнений.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ ВЕКТОРНАЯ АЛГЕБРА ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. Определения. — Прямая, на которой определено направление, называется осью. — Отрезок на оси, ограниченный точками А и В, называется направленным, если определено, какая из этих точек считается его началом, какая концом. — Направление отрезка — направление от его начала к его концу. Обозначается направленный отрезок — Величиной АВ направленного отрезка | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ .
.

 14.
14. 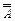 = A
= A Ì U — очевидно, так как U — универсальное множество.
Ì U — очевидно, так как U — универсальное множество. на число l называется вектор l
на число l называется вектор l  .
.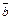 =
=  ) = (
) = ( ) и
) и ), то
), то  ), l
), l  = (
= ( ).
).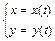 для линии на плоскости или
для линии на плоскости или 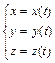 для линии в пространстве. При разных значениях параметра t получаем разные точки заданной линии. Можно использовать также векторное параметрическое уравнение линии:
для линии в пространстве. При разных значениях параметра t получаем разные точки заданной линии. Можно использовать также векторное параметрическое уравнение линии: 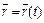 , где
, где  — радиус-вектор точки линии, определяемой значением параметра t.
— радиус-вектор точки линии, определяемой значением параметра t. (A; B). Требуется найти уравнение прямой, проходящей через точку М 0 перпендикулярно вектору
(A; B). Требуется найти уравнение прямой, проходящей через точку М 0 перпендикулярно вектору 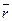 и
и  — ради- усы-векторы точек М и М 0. Вектор
— ради- усы-векторы точек М и М 0. Вектор  лежит на прямой и, следовательно, ортогонален вектору
лежит на прямой и, следовательно, ортогонален вектору  –
–  )·
)·  — вектор нормали,
— вектор нормали, , — вектор нормали.
, — вектор нормали. ; L 1 ^ L 2 Û
; L 1 ^ L 2 Û  .
. =
=  ,
,  — направляющий вектор,
— направляющий вектор, =
=  ,
,  — направляющий вектор.
— направляющий вектор. ê=
ê=  =
=  .
.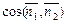 ê=
ê=  =
= 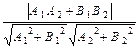 .
. =
=  .
. — радиусы-векторы точек М и М 0. Вектор
— радиусы-векторы точек М и М 0. Вектор 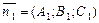 — вектор нормали,
— вектор нормали, , — вектор нормали.
, — вектор нормали. ; P 1 ^ P 2 Û
; P 1 ^ P 2 Û 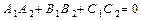 .
. — вектор нормали,
— вектор нормали, ê=
ê=  .
. =
=  =
=  с направляющим вектором
с направляющим вектором  . Напомним, что
. Напомним, что  .
. – j либо смежному с ним тупому углу. Поэтому sin j =
– j либо смежному с ним тупому углу. Поэтому sin j = 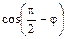 = ê
= ê  ê=
ê= 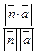 =
= .
. .
. не превышает
не превышает  , то данное условие можно переписать в виде
, то данное условие можно переписать в виде  , что равносильно неравенству
, что равносильно неравенству 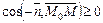 Û –
Û – 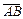 .
.